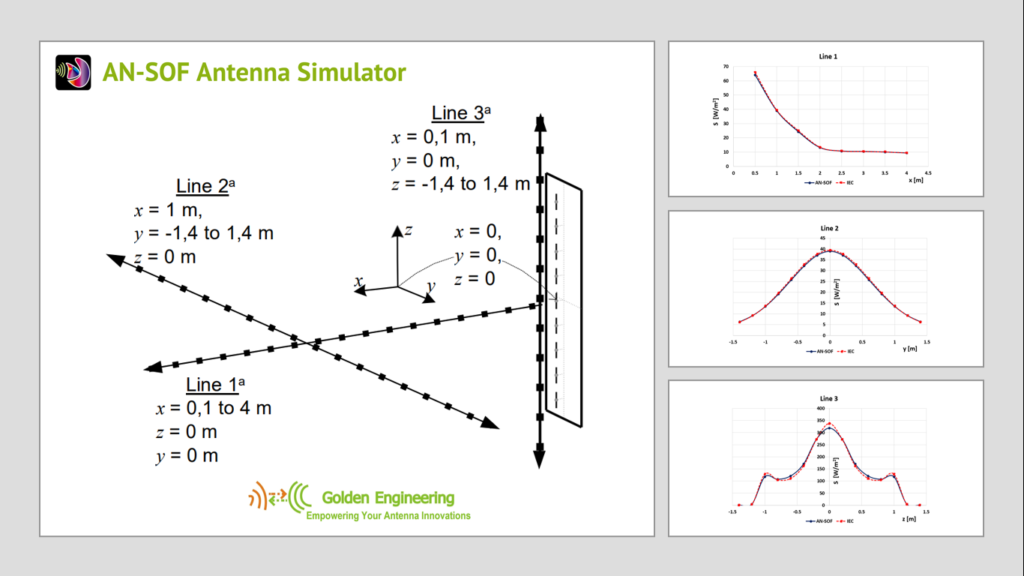
AN-SOF Passes IEC Validation
From version 8.20, the AN-SOF calculation engine has successfully completed validation for accuracy in accordance with the standard IEC FDIS 62232. This standard outlines guidelines for calculating radio-frequency field strength and specific absorption rate (SAR) in the vicinity of radiocommunication base stations (RBS) to assess the potential human exposure.