Here we present a summary of the top 5 posts from this past year. Don’t miss it!

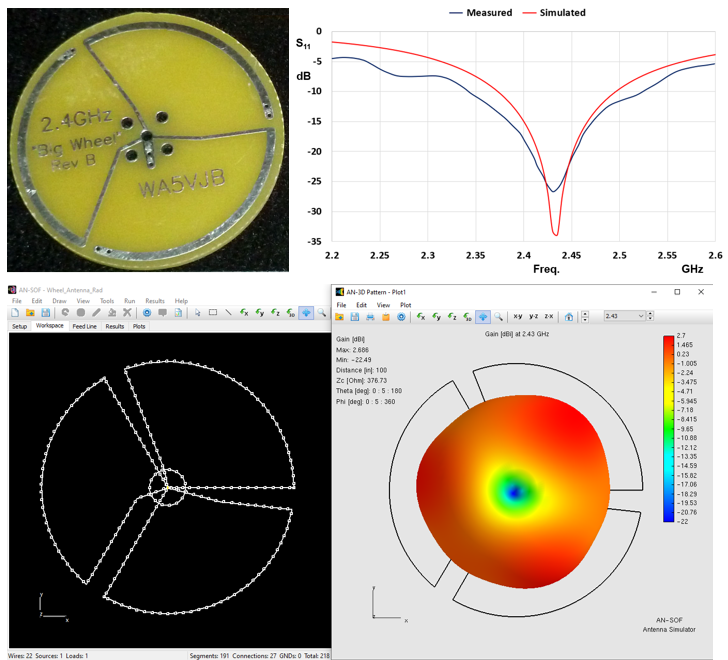
🥇 Accurate Analysis of Solid Wheel Antennas at 2.4 GHz Using Cost-Effective Simulation

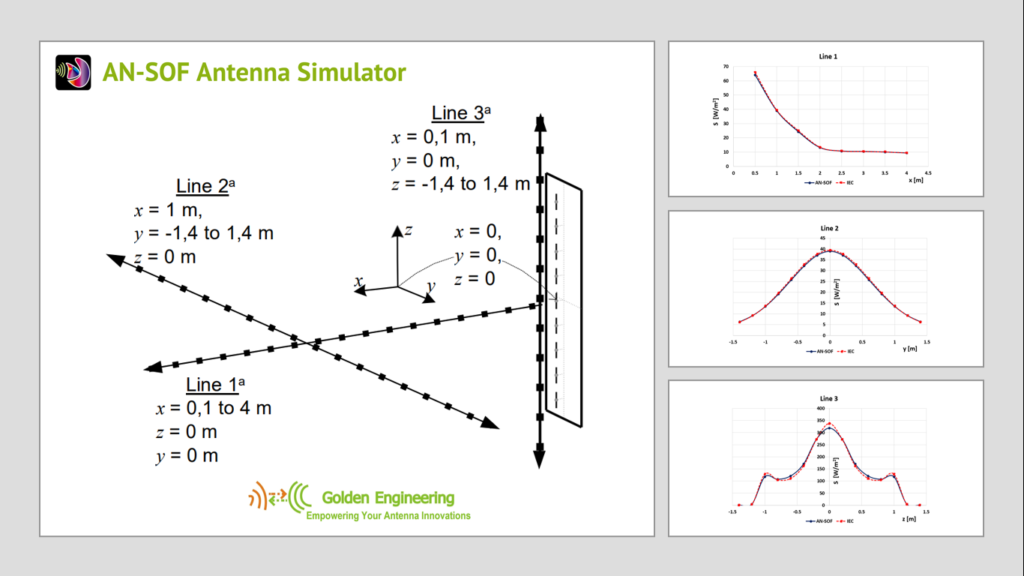
🥈 Evaluating EMF Compliance – Part 1: A Guide to Far-Field RF Exposure Assessments

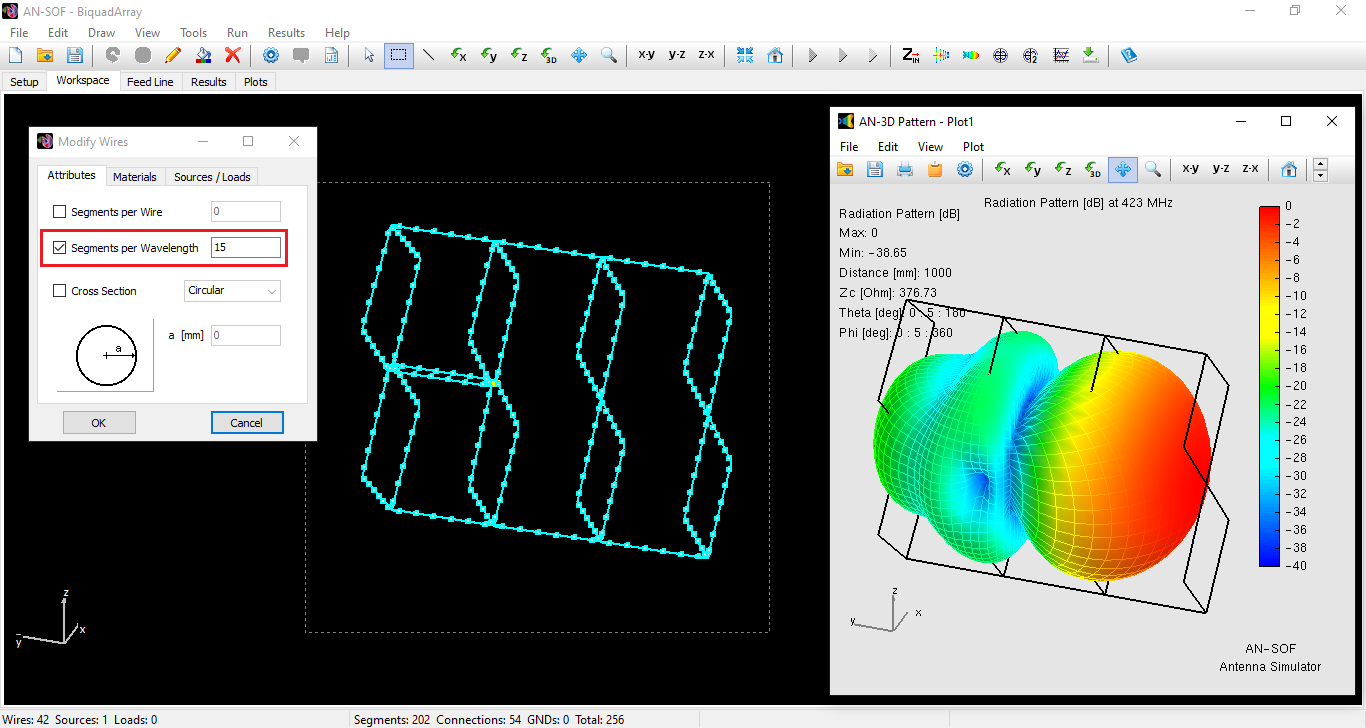
🥉 Design Guidelines for Skeleton Slot Antennas: A Simulation-Driven Approach

4️⃣ Efficient NOAA Satellite Signal Reception with the Quadrifilar Helix Antenna

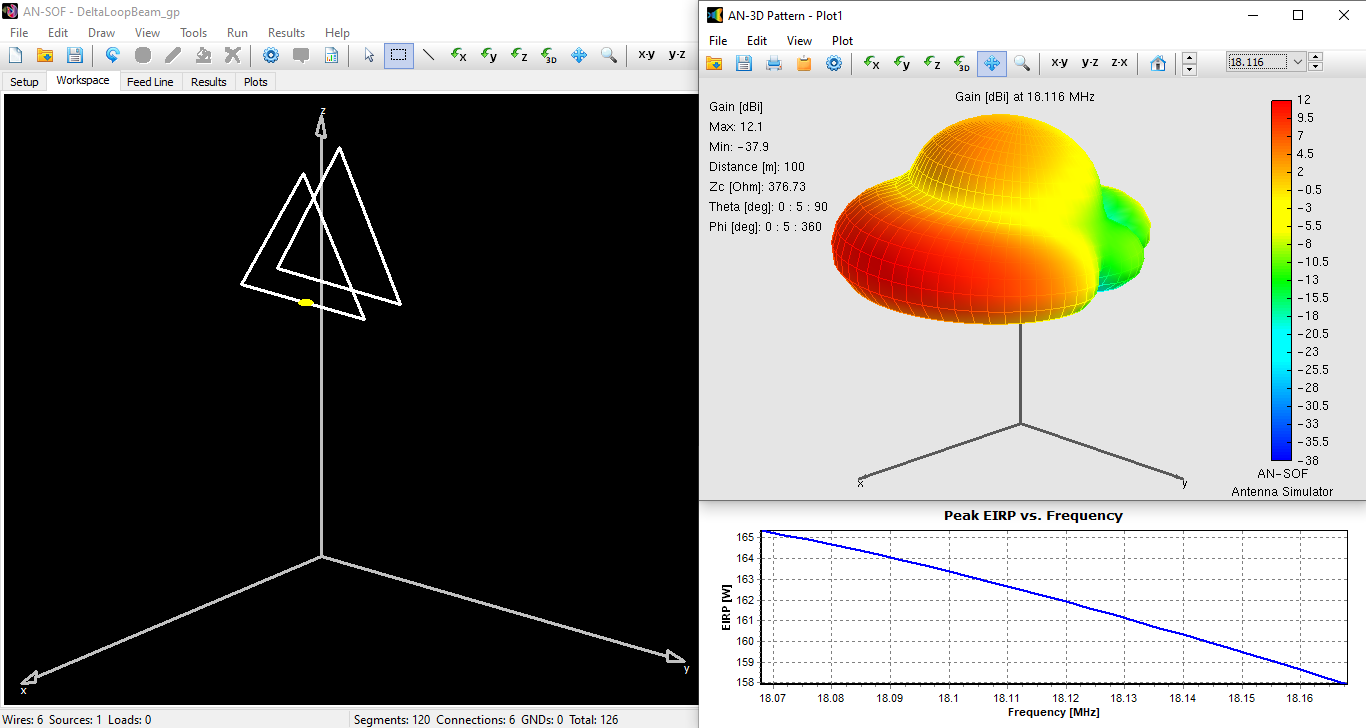
5️⃣ The Loop on Ground (LoG): A Compact Receiving Antenna with Directional Capabilities

Merry Christmas and Happy New Year from Golden Engineering!

Wishing you prosperity and success in 2024. 🥂

Exciting update! AN-SOF 8.90 is here with features like “Segments per Wavelength,” enhanced wire scaling, TL command import/export, and faster current distribution algorithms. Elevate your antenna simulations!

In today’s wireless world, ensuring Electromagnetic Field (EMF) compliance is crucial for protecting individuals from potential harmful effects of RF exposure. Join us as we explore the influence of antenna configurations, ensuring you possess the tools to navigate the complexities of EMF compliance effectively.

Revolutionize antenna modeling with our simplified method. Accurately simulate 2.4 GHz wheel antennas for optimal performance.

The Front-to-Rear ratio is a crucial factor in determining the directional performance of your antenna. AN-SOF can display this ratio in various forms. Discover the difference between the Front-to-Rear and Front-to-Back ratios in this article.