Accurate Analysis of Solid Wheel Antennas at 2.4 GHz Using Cost-Effective Simulation

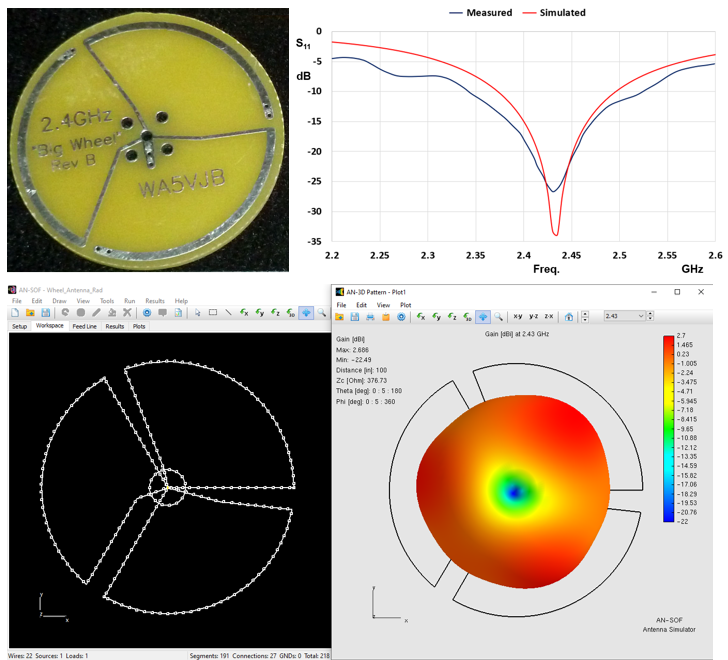
This article presents the calculated results for return loss and gain in the 2.4 GHz band for Wheel antennas. By employing a simplified method to simulate planar antennas on ungrounded dielectric substrates with sufficiently high permittivity, we can accurately replicate the measured data published by the Wheel antenna manufacturer, making it a valuable resource for engineering applications. A summary of the obtained results is provided in Figure 1. Not only is this method straightforward, but it also facilitates the utilization and expansion of cost-effective simulation software tools.

Introduction

Wheel antennas derive their name from their circular configuration and the presence of spokes akin to a cartwheel. Among wheel antenna designs, solid wheel antennas feature flat metallic traces printed on a singular dielectric substrate. Typically, these substrates are circular and crafted from materials such as FR4. Solid wheel antennas are known for their compact dimensions and frequent application in ISM (industrial, scientific, and medical) frequency bands spanning from approximately 900 to 2400 MHz, primarily within wireless network contexts. In the plane of the wheel, these antennas offer omnidirectional coverage and exhibit horizontal polarization. Moreover, the radiation pattern in the plane perpendicular to the wheel closely resembles that of a magnetic dipole, taking on a distinctive donut-like shape.

This article centers on the examination of a 2.4 GHz wheel antenna manufactured by Kent Electronics (WA5VJB). Our primary objective is to replicate the measured return loss data (S₁₁) for the Big Wheel Rev B antenna variant as provided by the manufacturer, available at this link.

Calculation Method

Given the planar nature of wheel antennas, fabricated on an ungrounded dielectric substrate, we can employ a straightforward method for simulating these microstrip antennas. This approach is outlined in the article Simplified Modeling for Microstrip Antennas on Ungrounded Dielectric Substrates: Accuracy Meets Simplicity, which offers a cost-effective means of modeling such antennas. This methodology capitalizes on the capabilities of wire antenna simulation software, such as AN-SOF.

The initial step involves defining the frequency range of interest, which, in this instance, spans from 2.2 to 2.6 GHz. Subsequently, the antenna structure is created within AN-SOF. This process is relatively uncomplicated and entails the addition of Line objects to represent the straight metallic strips and Arc objects to replicate the curved sections of the antenna. This wheel antenna boasts a diameter of approximately 1.5 inches. At the center of this circular structure, the feed point is positioned.

Radiating outward from the antenna’s center, there are spokes that connect to the arcs on the antenna’s periphery, situated above the dielectric substrate. Additionally, there are spokes that return beneath the substrate to close the electrical circuit of the antenna. For the sake of facilitating external connectivity, the manufacturer typically incorporates a coaxial connector at the antenna’s central point, enabling a straightforward connection to a coaxial cable.

AN-SOF, operating on the Conformal Method of Moments, mandates the division of wires into shorter segments relative to the wavelength. In the case of the antenna printed on FR4, which possesses a dielectric constant of 4.6, the applicable wavelength must be that of free space divided by √(4.6) = 2.14. Consequently, for the uppermost frequency within the specified range, 2.6 GHz, the wires have been partitioned into segments measuring 2% of the wavelength within the substrate. This aligns with the same criterion employed for planar dipoles, as detailed in the previously referenced article.

In accordance with the manufacturer’s datasheet, this antenna is tunable through the introduction of a capacitor with an approximate value of 1 pF. This tuning capacitor has been incorporated into the model at the feed point, inserted in series with a voltage source. By configuring a medium characterized by a permittivity of 4.6, as depicted in Figure 2, and initiating the calculations with a Ctrl + R command, we have ascertained that the antenna resonates at 2.43 GHz when equipped with a 0.7 pF capacitor, consistent with the datasheet’s specifications. Consequently, there is no necessity to determine the resonance frequency in free space, as elucidated in the simplified method. This instance exemplifies an alignment between the effective permittivity and the substrate’s permittivity.

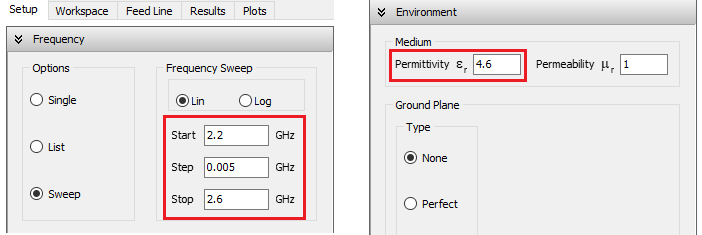
Figure 3, included below, presents a photograph of the physical wheel antenna, sourced from the manufacturer’s website, alongside the corresponding AN-SOF model, illustrating the employed segment density.

Comparison with Measured Data

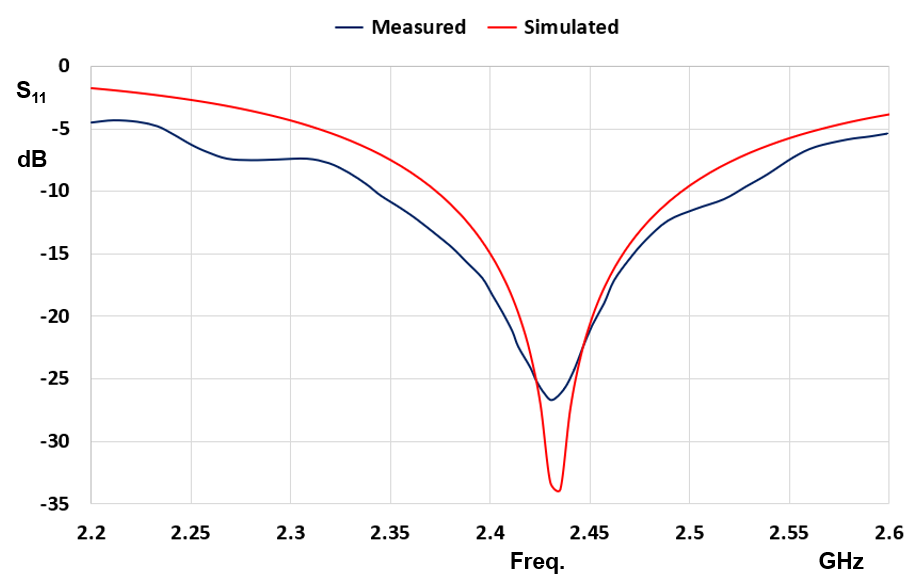
Initiating the input impedance calculation with a Ctrl + R command, within the scrutinized frequency span of 2.2 to 2.6 GHz and employing a medium permittivity of 4.6, we generate the S₁₁ curve presented in Figure 4. This figure also overlays the measured S₁₁ curve, extracted from the manufacturer’s datasheet. It is evident that the agreement between the simulated and measured outcomes is remarkably robust, particularly in the vicinity of the resonance frequency. It is noteworthy that this model’s remarkable accuracy persists despite the simplification that completely disregards the dielectric substrate’s thickness and contour.

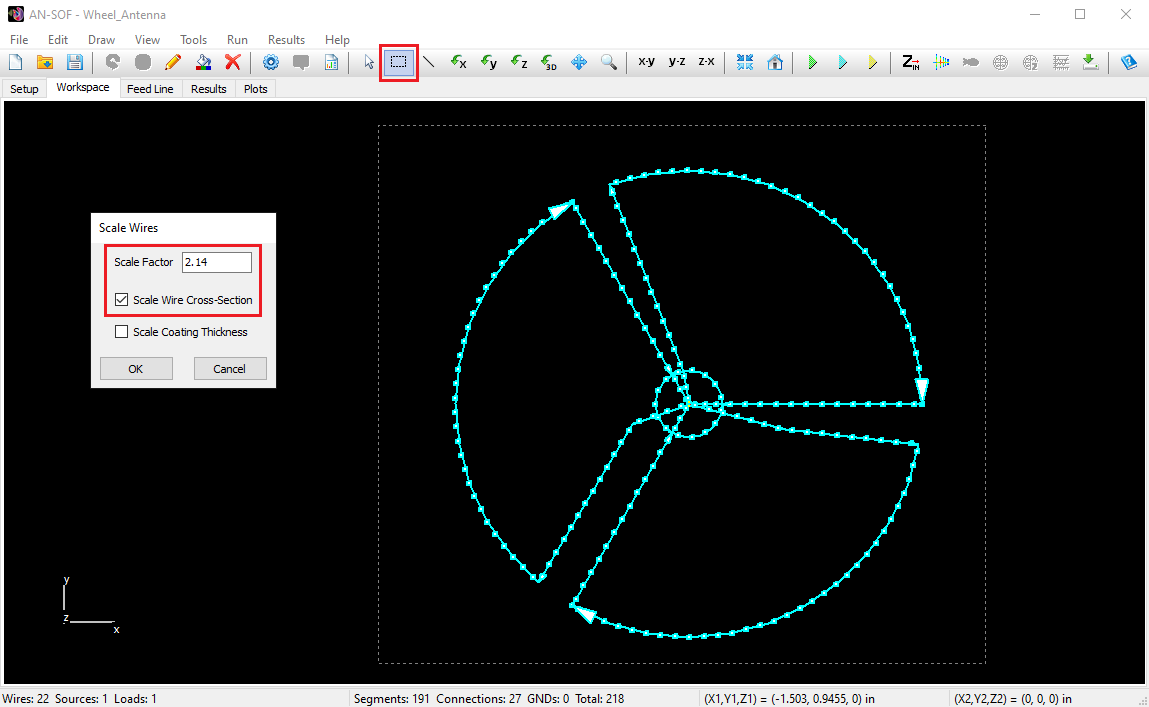
To calculate the radiation pattern, we must set the permittivity of the medium (free space) to 1, and then rescale the antenna’s dimensions by a factor of √(4.6) = 2.14. This can be achieved by first clicking on the “Selection Box” button within the AN-SOF toolbar. Subsequently, draw a box around the entire antenna using the mouse and then proceed to Edit > Scale Wires in the main menu. Here, input the scaling factor of 2.14, ensuring that you adjust the wire cross-section accordingly, as depicted in Figure 5. Furthermore, it is necessary to modify the value of the tuning capacitor, reducing it from 0.7 pF to 0.7/2.14 = 0.33 pF.

Once these adjustments are made, the calculation is tailored to the single frequency of 2.43 GHz, since our primary interest lies in the radiation pattern at the resonance frequency. With this configuration, we proceed with the calculations by pressing F11. The outcome, illustrated in Figure 6 (left), portrays the gain pattern in decibels (dBi), which, as anticipated, exhibits near-omnidirectional coverage within the plane of the antenna. Furthermore, the polarization is predominantly horizontal, evident from the dominance of the E_φ (azimuthal) component over the E_Θ (zenithal) component of the electric field, as shown in Figure 6 (right). The E_φ component of the electric field reveals that there are three directions with radiation peaks, corresponding to each wheel arch, indicating that the radiation pattern is not perfectly omnidirectional.

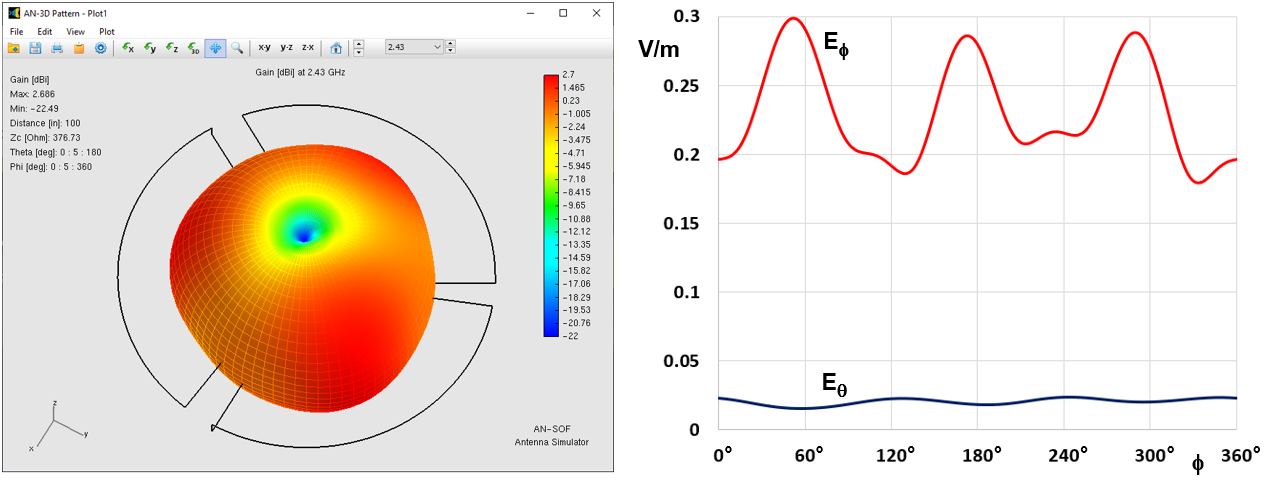
The calculated peak gain registers at 2.7 dBi, slightly surpassing the manufacturer’s specification of 2 dBi. It is essential to acknowledge that this computed gain does not account for all potential power losses within the actual antenna, particularly within components such as the coaxial connector and the substrate (incorporating loss tangent). These factors have been omitted in our model, wherein solely a resistivity matching that of aluminum has been introduced for the metal traces.

Conclusions

In this article, we have introduced a simplified method for the modeling of solid wheel antennas, enabling the calculation of their return loss and radiation pattern. We have employed this method to simulate the performance of the Big Wheel Rev B antenna designed for the 2.4 GHz band, as provided by Kent Electronics. The results obtained through AN-SOF simulation have been compared with the measured data furnished by the manufacturer, and a high degree of agreement has been achieved.

This study serves as a clear demonstration of AN-SOF’s efficacy in modeling planar antennas that are printed on ungrounded dielectric substrates, specifically substrates like FR4. The method presented here not only offers simplicity but also demonstrates remarkable accuracy, highlighting its value for antenna engineers and researchers seeking cost-effective, reliable antenna design and analysis tools.