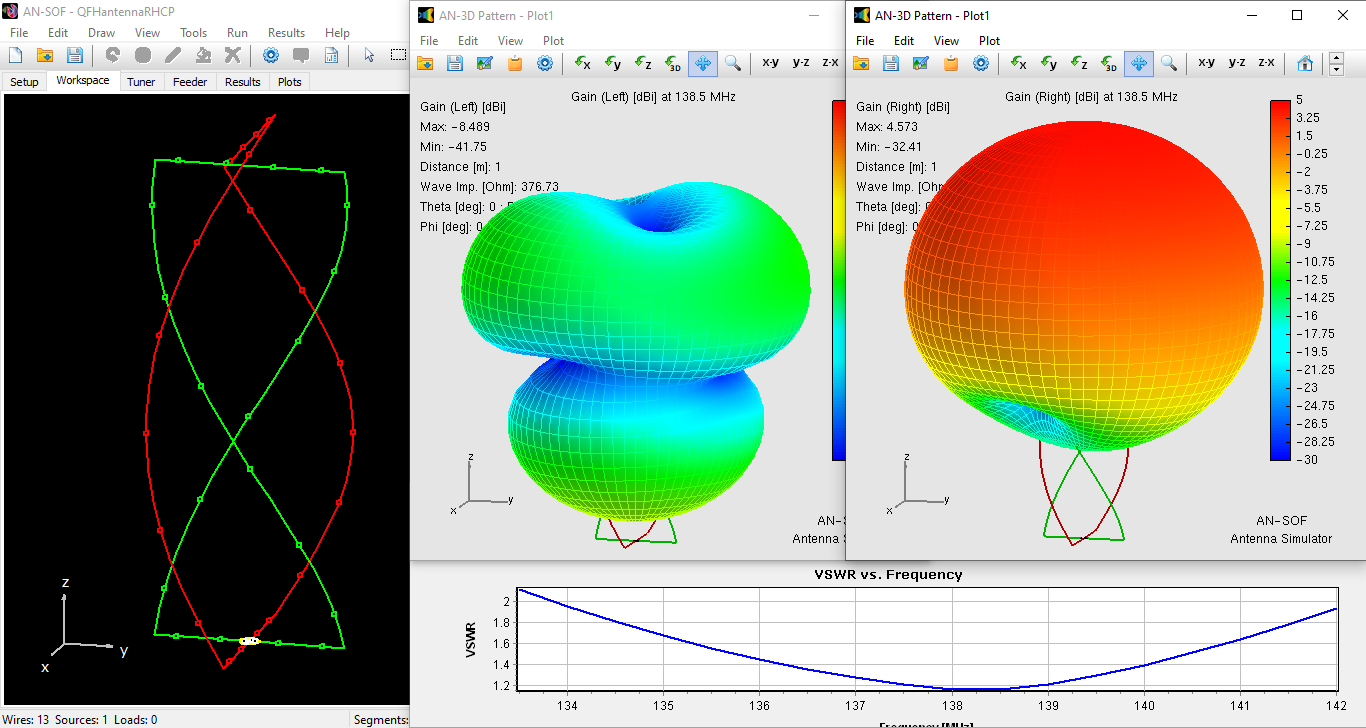
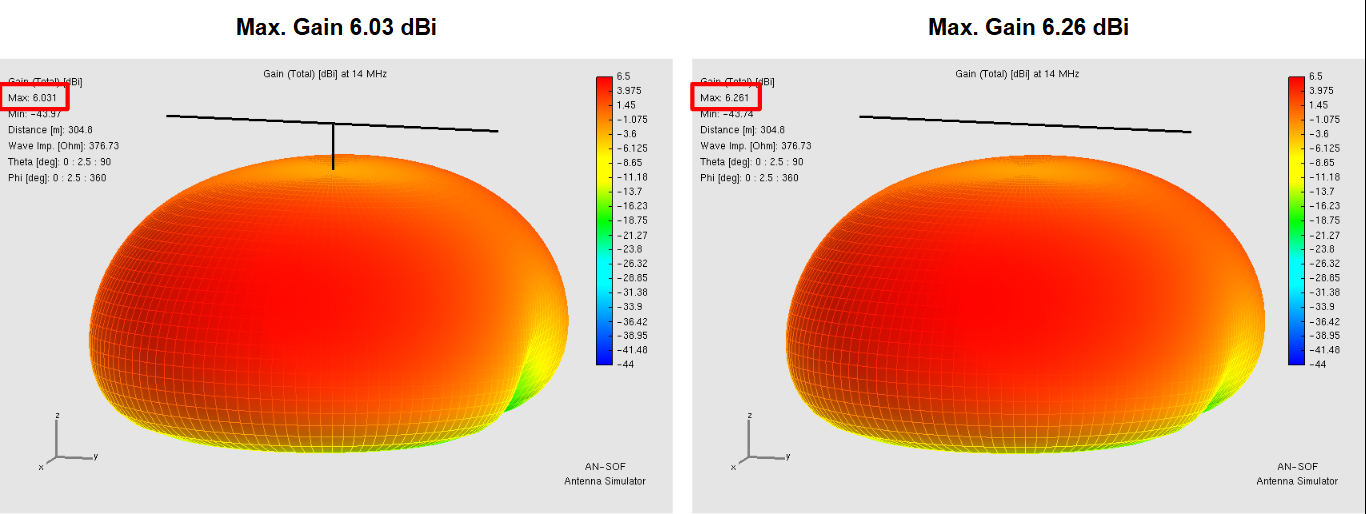
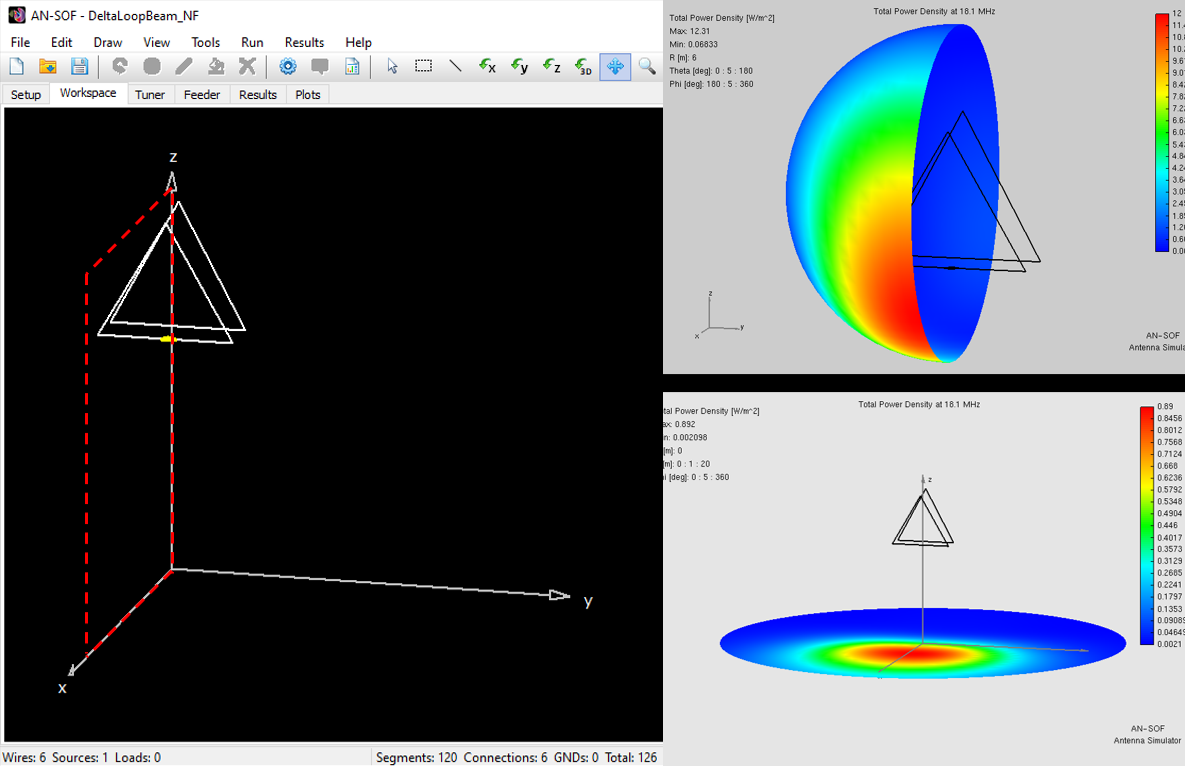
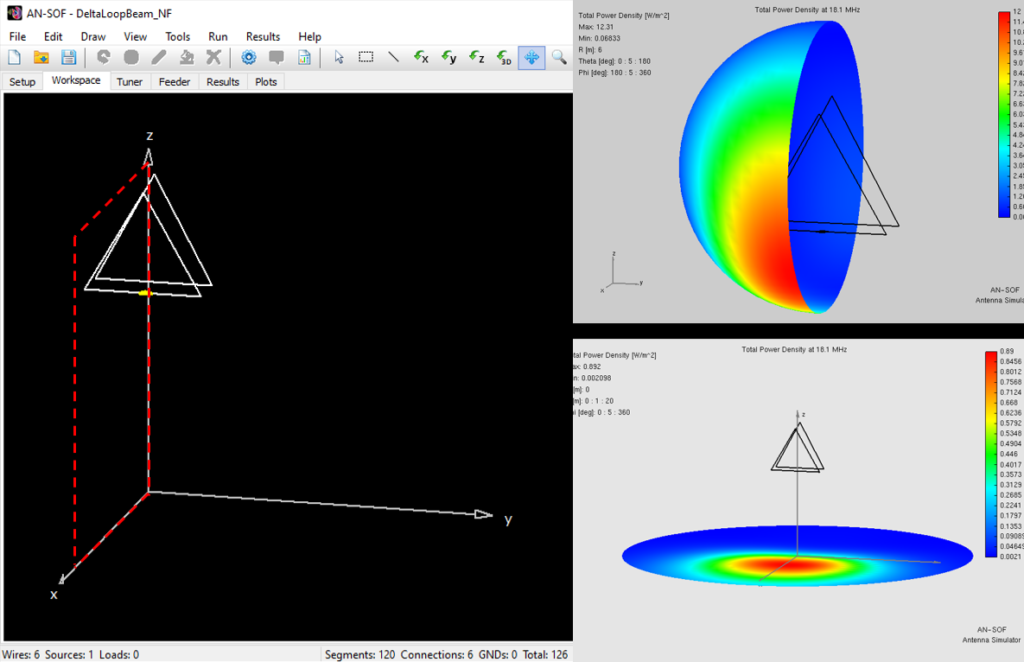
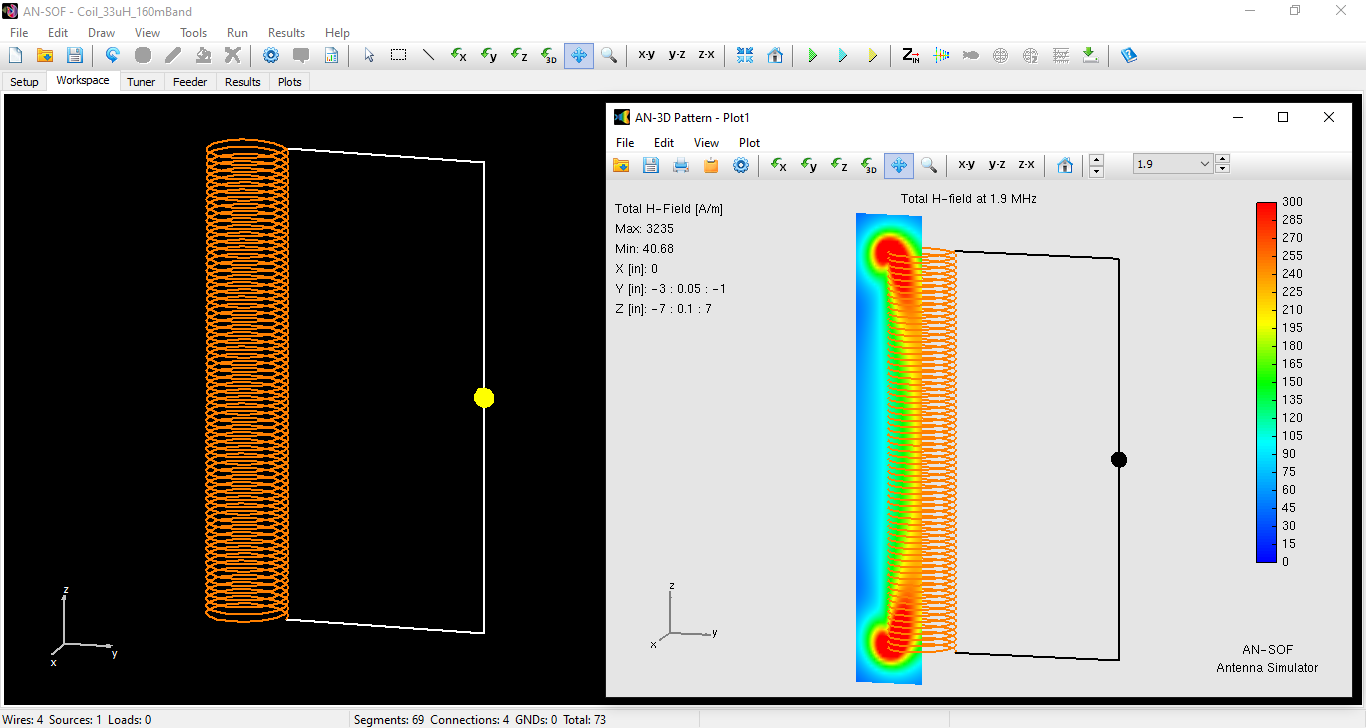
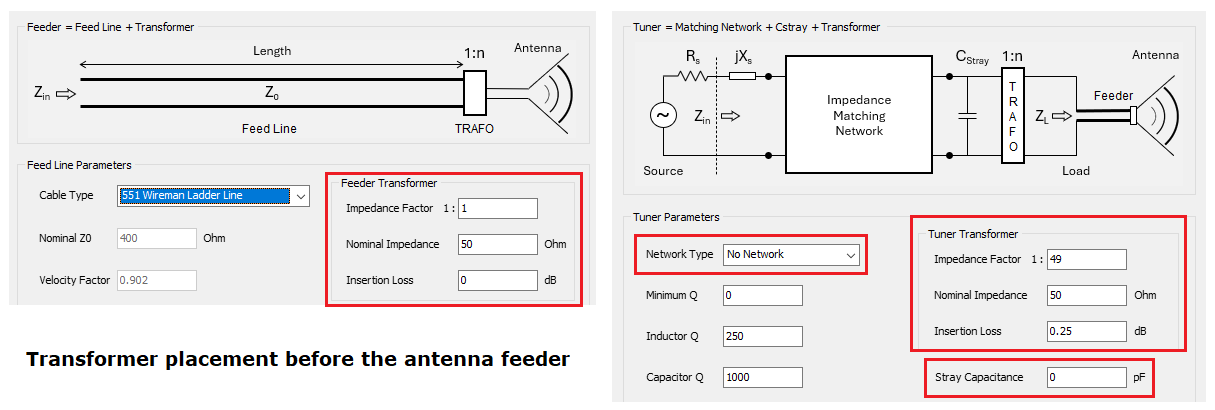
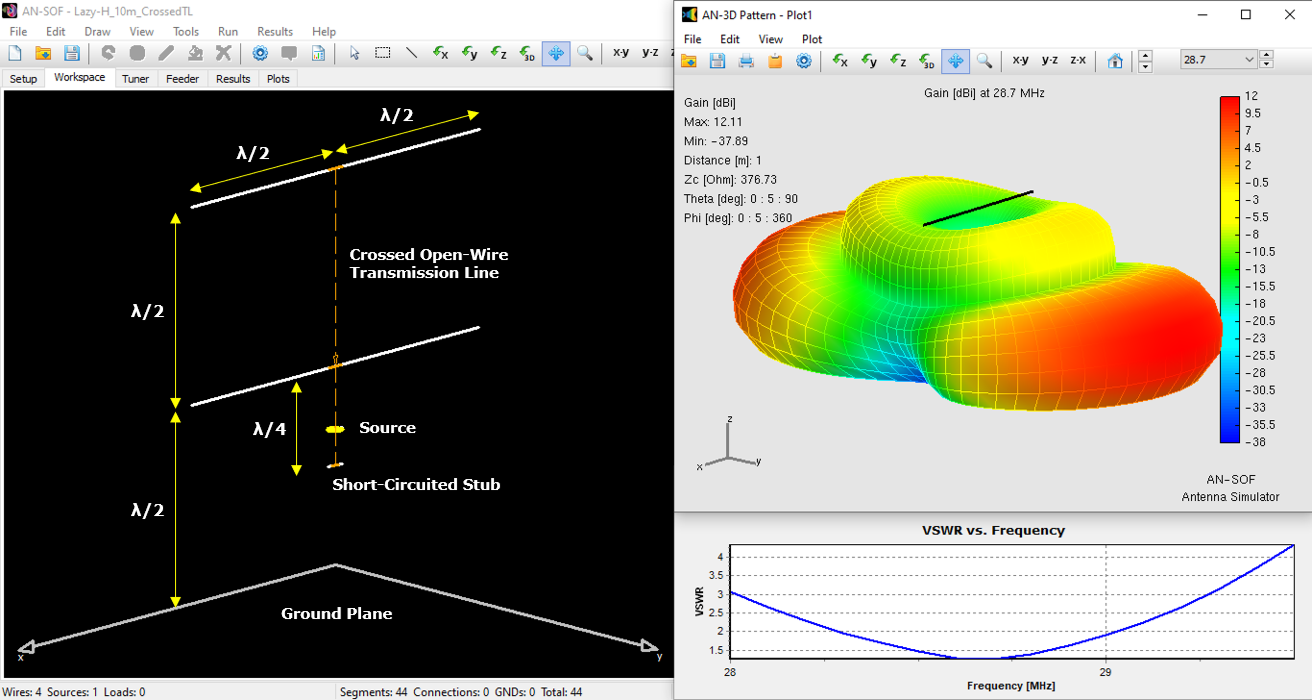
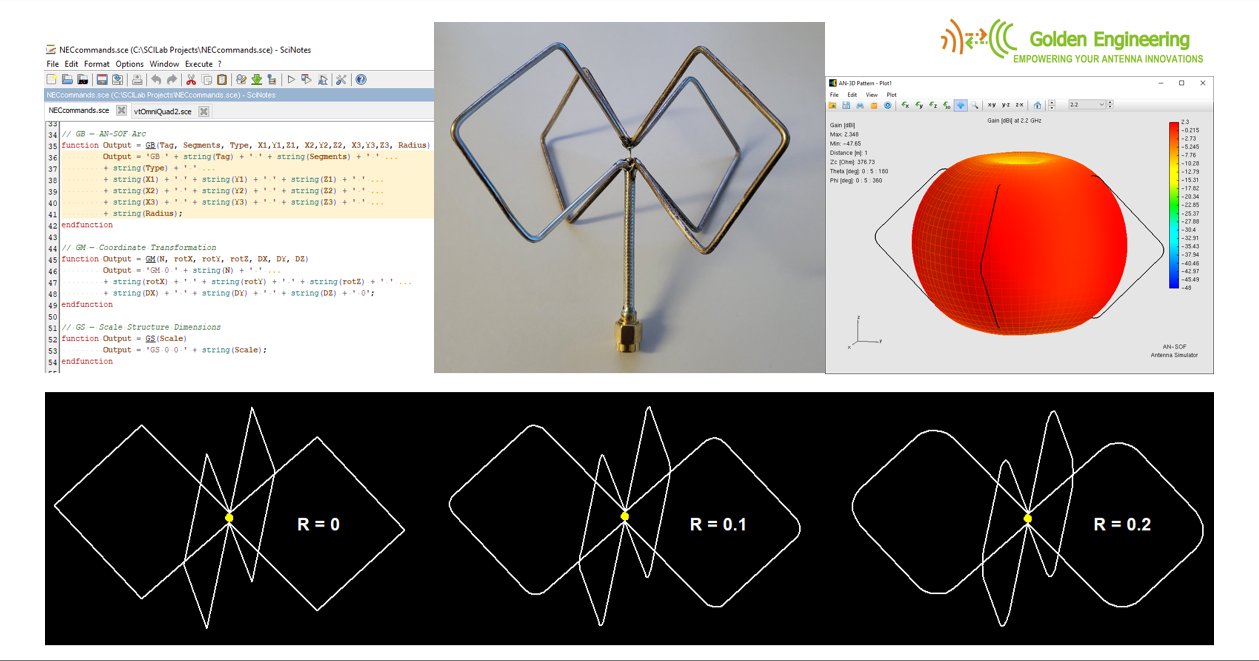
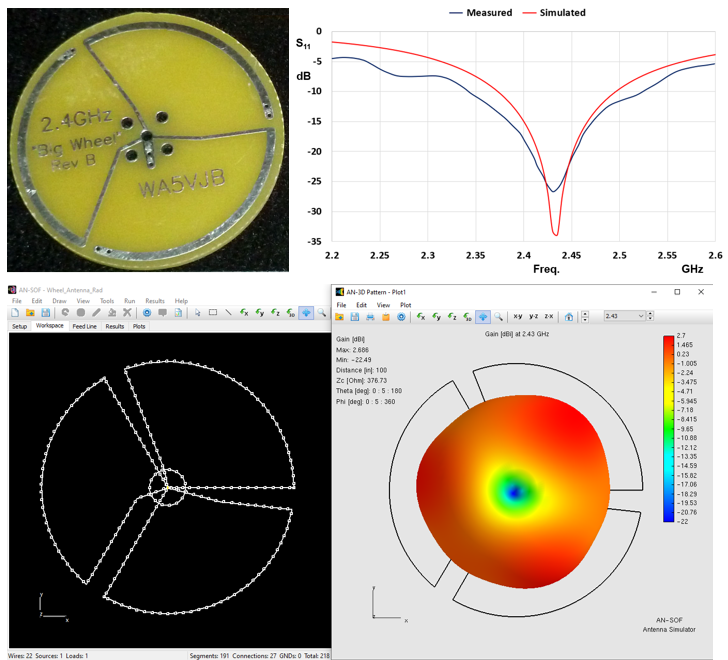
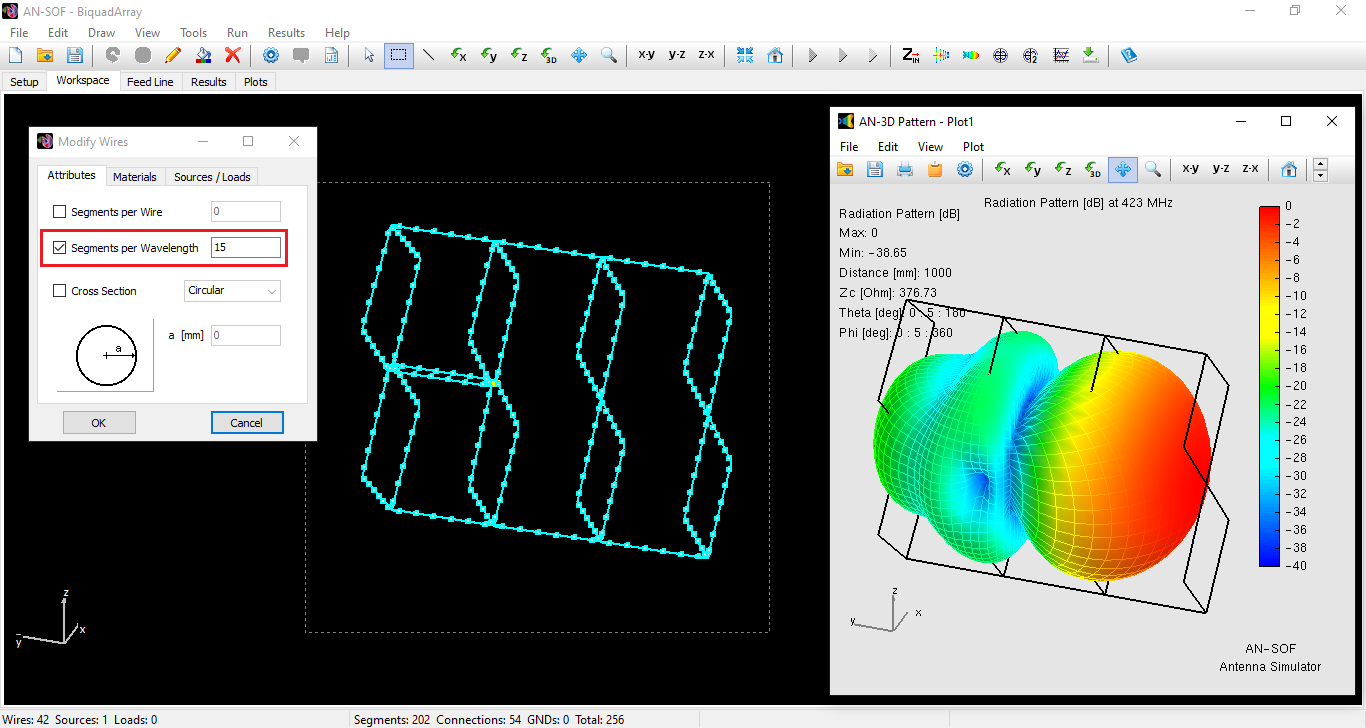
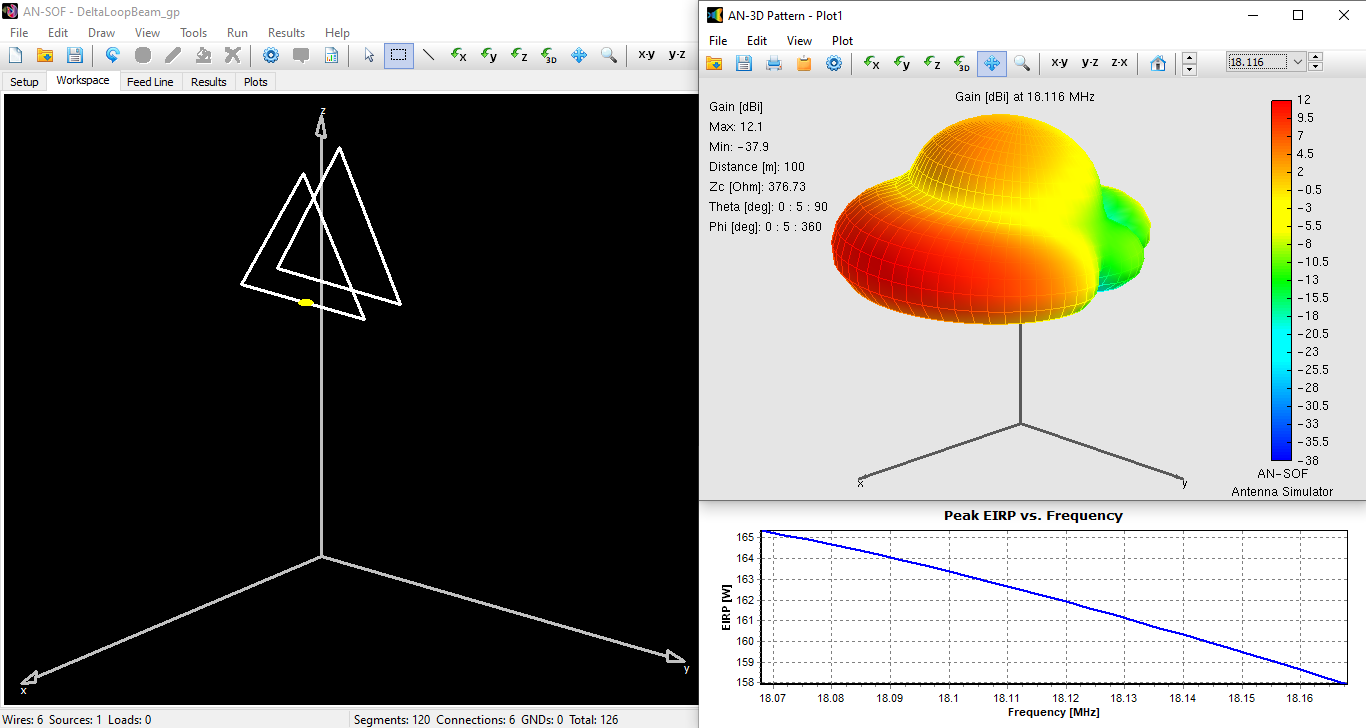
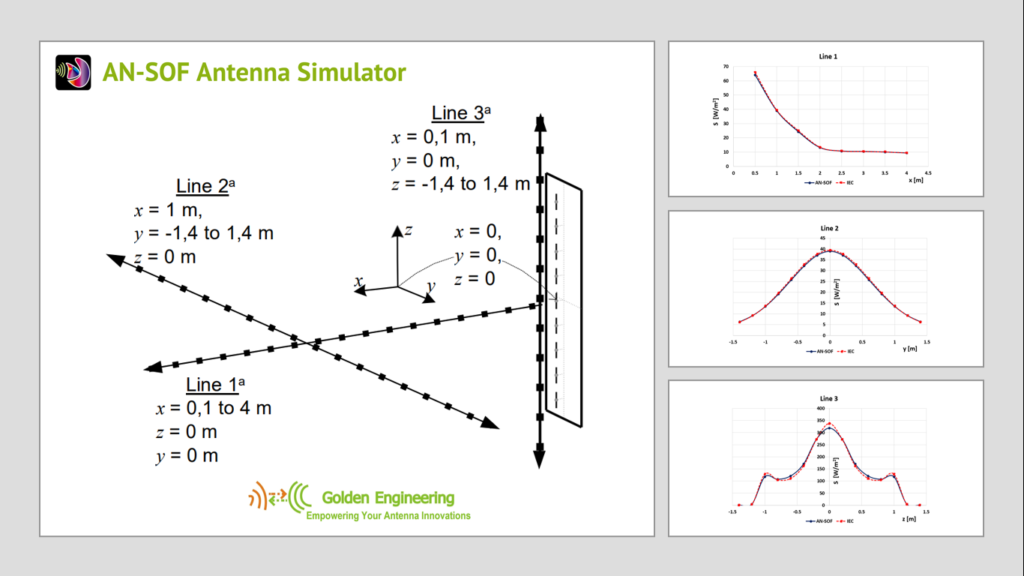
Modeling BoG Antennas in AN-SOF – Coming Soon!
Beverage-on-Ground (BoG) antennas are commonly used to receive signals from VLF up to the lower HF band. They consist of one or two wires laid directly on the ground. While their proximity to the ground can increase losses, BoGs offer key advantages: they are easy to install and require less space than elevated Beverage antennas to achieve the same electrical length.
Despite their simplicity, accurately modeling BoGs can be challenging—and there are still many open questions among the BoG enthusiast community.
That’s why I’m excited to share that I’ll soon be publishing an article on how to model BoG antennas in AN-SOF, using a simple, fast, and sufficiently accurate approach inspired by transmission line theory.
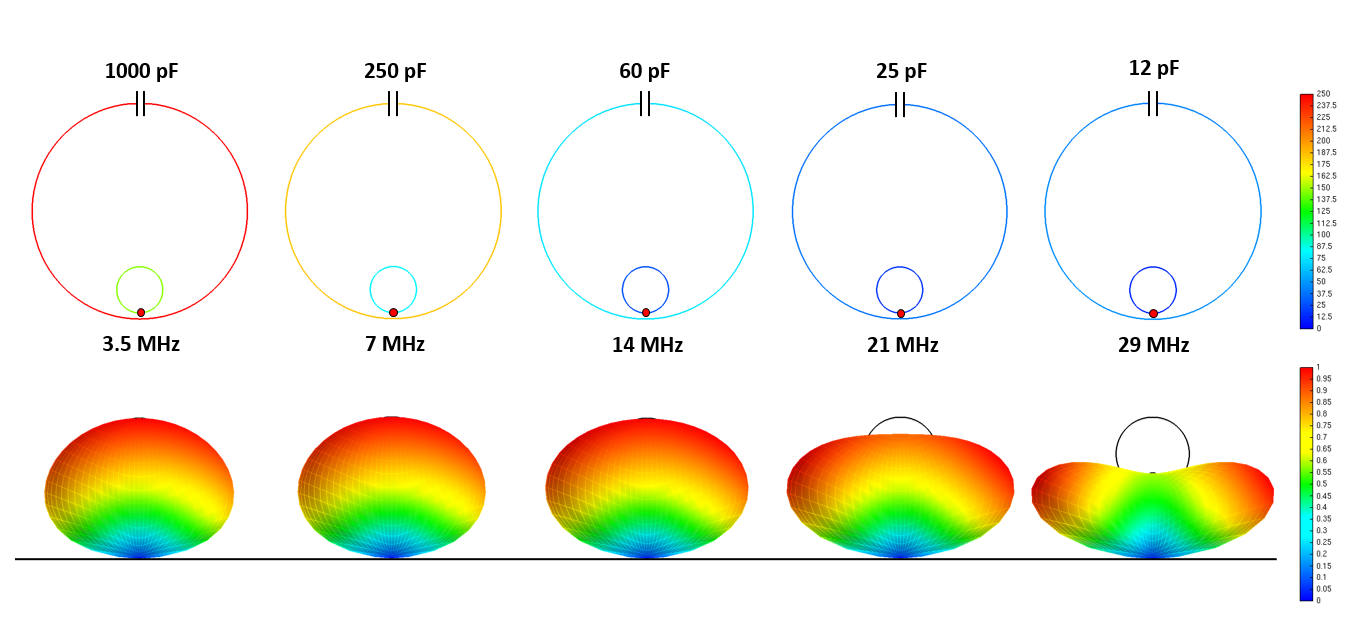
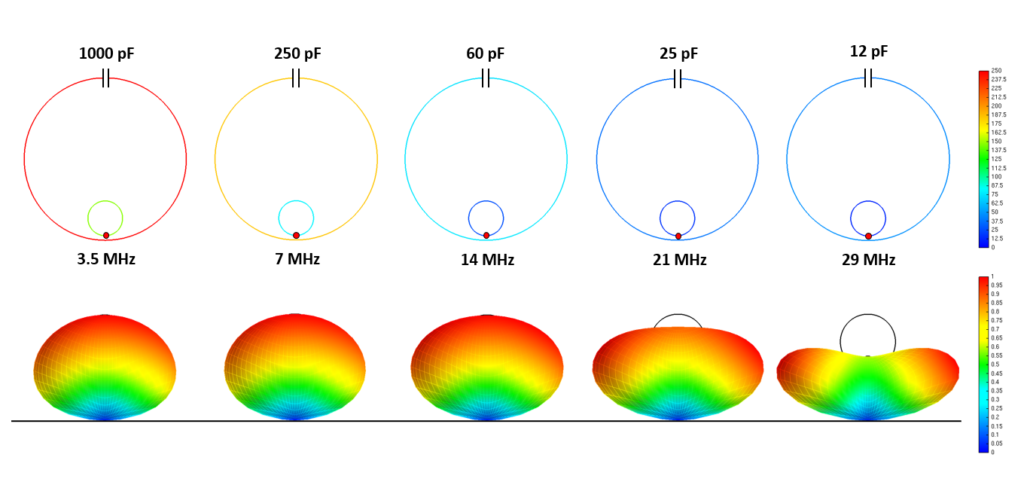
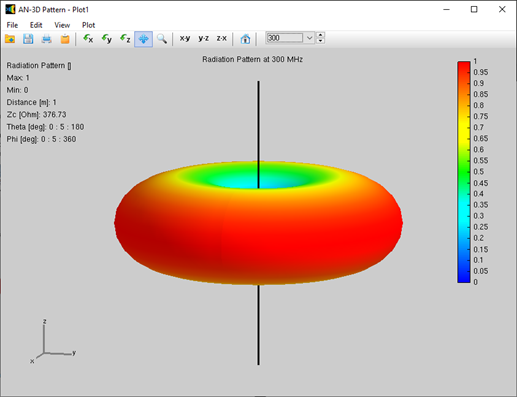
The animation below shows the directivity pattern of a 450-ft BoG modeled in AN-SOF, from 1 to 4 MHz. As expected, secondary lobes become more prominent with increasing frequency. One key insight: the front-to-back ratio can be optimized by adjusting the wire length—and if the wire is long enough, you may not need a termination resistor at all.

AN-SOF provides a powerful modeling tool to visualize, understand, and optimize BoG antennas based on real-world behavior.
Special thanks to our customer Richard Kunath (K9AO) for bringing this fascinating topic to my attention and generously sharing his insights and archives. His contributions helped make this deep dive possible.
— Tony