Logarithmic Spiral

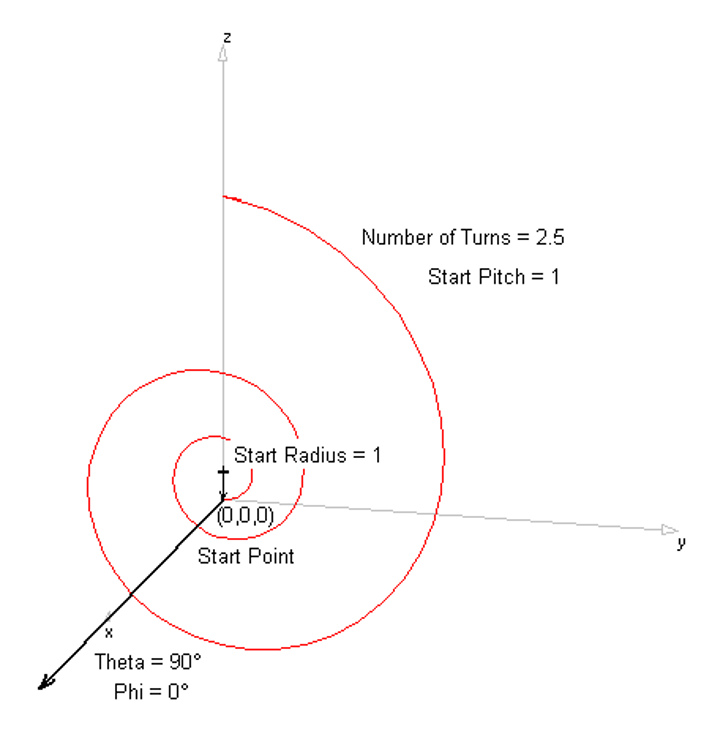
A Logarithmic Spiral represents an equiangular spiral in AN-SOF.

The logarithmic spiral (spira mirabilis) is defined by the polar equation:

$\displaystyle r(\alpha) \,=\, r_0 \, e^{b \alpha}$

where $r_0$ is the starting radius (the value of $r$ at $\alpha = 0$) and $b$ is a constant given by:

$\displaystyle b \,=\, \frac{p}{2\pi r_0}$

In this expression, $p$ represents the starting pitch, which is the derivative of the radius at the origin:

$\displaystyle p \,=\, 2\pi \, \frac{dr}{d\alpha} \bigg|_{\alpha \,=\, 0}$

This value $p$ corresponds to the initial growth rate of the spiral radius $r(\alpha)$ per turn. The angle $\alpha$ ranges from $0$ to $2\pi M$, where $M$ is the number of turns.

The first three terms of the Taylor expansion of the radius around $\alpha = 0$ are:

$\displaystyle r(\alpha) \,=\, r_0 \,+\, \frac{p}{2\pi} \alpha \,+\, \frac{r_0 (b \alpha)^2}{2} \,+\, \dots$

The linear portion of this expansion ($r_0 + p/(2\pi) \, \alpha$) provides the polar equation of an Archimedean spiral.

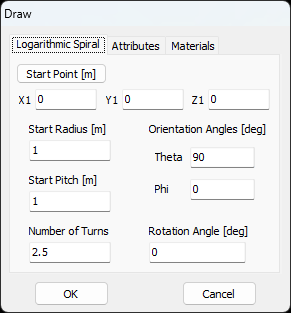
Accessing the Logarithmic Spiral Dialog Box

To open the Logarithmic Spiral dialog box:

1. Navigate to Draw > Logarithmic Spiral in the main menu.
2. The dialog box contains three tabs: Logarithmic Spiral, Attributes, and Materials (Fig. 1).

Logarithmic Spiral Tab: Setting Geometrical Parameters

Define the logarithmic spiral by specifying the following (Fig. 1):

• Start Point: Starting coordinates (X1, Y1, Z1).
• Start Radius: The initial radius of the spiral at the starting point.
• Start Pitch: The initial pitch (turn spacing) of the spiral; this value can be positive or negative.
• Number of Turns: The total number of turns; this does not need to be an integer, allowing for fractional turns.
• Orientation Angles: Sets the direction of the spiral axis using spherical angles (Theta, Phi).
• Rotation Angle: Rotates the spiral around its axis.

Attributes Tab

• Specify the Number of Segments and Cross-Section properties (refer to Wire Attributes).

Materials Tab

• Set the Resistivity and Coating properties of the wire (refer to Wire Materials).