Enhanced Methodology for Monopoles Above Radial Wire Ground Screens

Monopole antennas have been extensively studied in the scientific literature, particularly during the first half of the 20th century, coinciding with the rise of radio communications in the LF and MF bands. In broadcasting applications, it is crucial to consider the impact of power losses in the Earth’s soil, as they directly affect both the antenna’s input impedance and efficiency.

In terms of the input impedance, it is directly influenced by the soil parameters in close proximity to the antenna. To artificially enhance soil conductivity, it is common practice to incorporate buried wires just beneath the soil surface. These buried wires typically take the form of radial screens, extending up to a quarter-wave or half-wavelength distance from the base of the monopole.

As monopoles are linear antennas, the methods employed to address the solution for a monopole positioned above a real ground plane, with a radial wire ground screen, are based on the findings obtained for cylindrical antennas in free space. Unfortunately, the availability of measured data is limited due to the experimental challenges involved in obtaining highly precise values in real-world installations. Monopole antennas in the LF and MF bands can reach heights ranging from tens to hundreds of meters. Nonetheless, numerical results can be compared with established analytical approaches, as described below.

Professor James R. Wait derived analytical expressions for calculating the input impedance of a monopole situated above a radial wire ground screen. However, these expressions take the form of reaction integrals that must be solved numerically. For more information, please refer to “Impedance of a Top-Loaded Antenna of Arbitrary Length over a Circular Grounded Screen” by James R. Wait and Walter J. Surtees, published in the Journal of Applied Physics (volume 25, page 553, 1954). On the other hand, L. A. Dorado was the first to develop simplified analytical equations for calculating the input resistance based on Poynting’s theorem and the determination of power loss in the soil beneath the antenna. Both approaches aim to quantify the increase in input impedance compared to the impedance that the monopole would exhibit if it were positioned above a perfectly conducting ground plane.

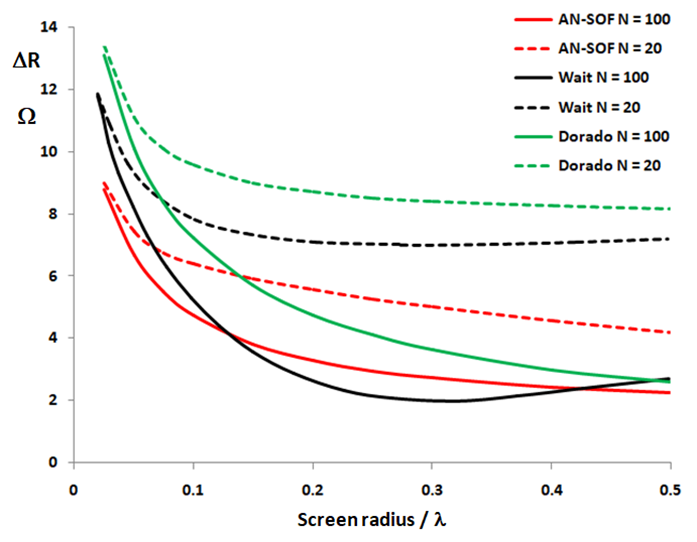
Figure 1 illustrates the increase in input resistance, ΔR, of a monopole antenna positioned above a radial wire ground screen, considering N = 20 and N = 100 radials, and an average soil condition, as a function of the screen radius. This figure presents a comparison among the results obtained using Wait’s, Dorado’s, and AN-SOF’s methodologies. The curves exhibit similarities, although a vertical shift is noticeable. This shift can be expected because Wait’s and Dorado’s approaches do not accurately account for the effect of the monopole radius. It is widely recognized that the finite radius of a cylindrical antenna significantly impacts its input impedance. Professor Wait approximated the monopole current distribution using a perfect sine function, corresponding to an infinitely thin vertical wire. Professor Dorado acknowledged this limitation and attempted to address it by applying a correction factor, which depends on the antenna’s height-to-radius ratio. In the case of AN-SOF, Poynting’s theorem is also utilized to compute the power lost in the soil, while accurately incorporating the effect of the finite radius of the antenna through the utilization of the Exact Kernel. Consequently, it can be concluded that AN-SOF represents an improvement over Dorado’s method.

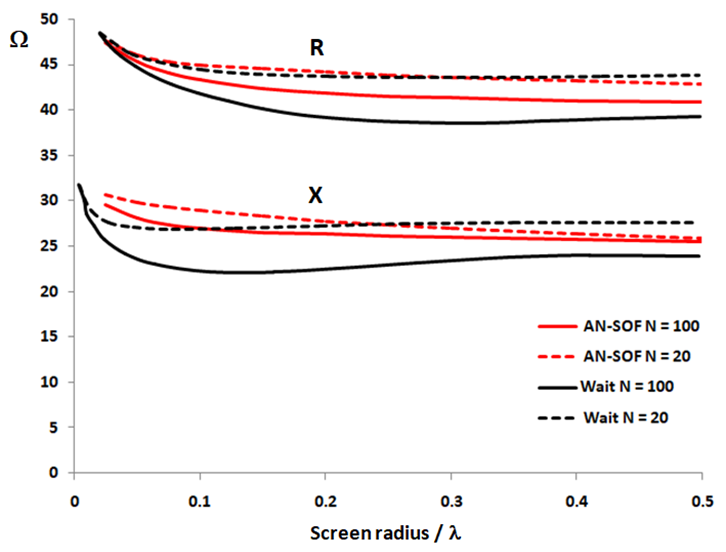
Furthermore, AN-SOF offers an additional advantage as it enables the determination of the imaginary part of the input impedance (i.e., the reactance), whereas Dorado’s method only allows for the calculation of resistance. Since the input reactance is also available in Wait’s approach, Figure 2 compares the results obtained using AN-SOF and Wait’s methods for the input impedance as a function of the screen radius. The presented results are highly satisfactory, particularly considering the computational challenges faced by Professor Wait during his time when performing such complex calculations.