Radiation Resistance and Directivity of Small Loops

Among the advantages of the Conformal Method of Moments (CMoM) > implemented in AN-SOF is the ability to model exactly the contour of curved antennas. Besides, calculations at extremely low frequencies are possible or, equivalently, when the antenna size is a tiny fraction of a wavelength. Both advantages will be demonstrated in this article for the small loop antenna.

One theoretical prediction for loop antennas whose size is much smaller than the wavelength is that the radiation resistance, R_r, is independent of the loop shape and it only depends on its area, A, measured in square wavelengths, λ², as follows:

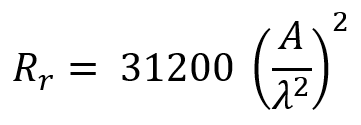
This equation must be interpreted as the limit of the radiation resistance when the loop size tends to zero. To get this equation it is also assumed that the current distribution along the loop circumference is uniform.

The computed radiation resistances of small circular and square loops are plotted in Fig. 1 as a function of frequency, as well as the theoretical prediction. Both loops have an area of 0.01 m² (square loop: 0.1 m x 0.1 m; circular loop: 0.05642 m in radius). For instance, the wavelength is λ = 3 m at 100 MHz, so the normalized loop area is A/λ² = 0.0011. As the frequency increases, the theoretical prediction departs from the simulation results because it is no longer valid.

Another theoretical prediction for small loops is that the directivity becomes independent of the loop size and even of frequency. The peak directivity is a contact, 3/2, the radiation pattern is doughnut-shaped and it has exactly the same expression as for a Hertzian dipole, namely,

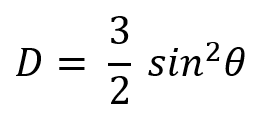
This equation must also be considered as a limiting case when the loop size measured in wavelength tends to zero. This can be seen in Fig. 2, where the peak directivity is represented as a function of frequency for the small circular and square loops simulated with AN-SOF, the horizontal asymptote being the theoretical result.

Fig. 3 shows the computed radiation patterns of the small circular and square loops at 30 MHz, and Fig. 4 shows a vertical slice of the patterns represented in a Cartesian chart. Only the radiation pattern for the circular loop is plotted in Fig 4 since the square loop results are so close to it that the difference cannot be seen with the naked eye.

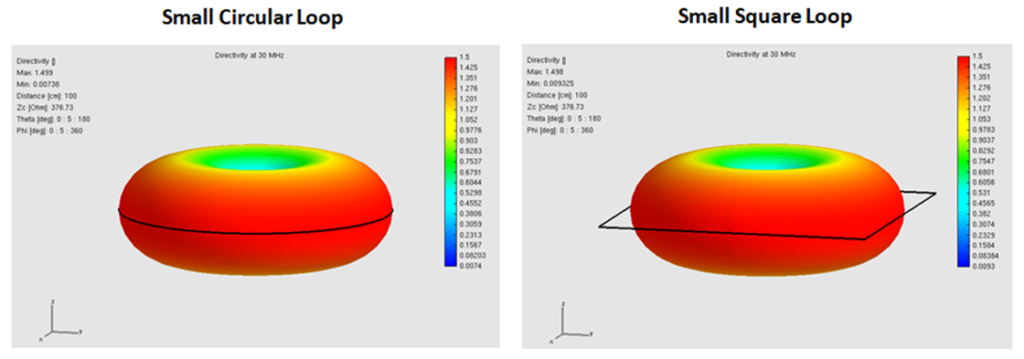
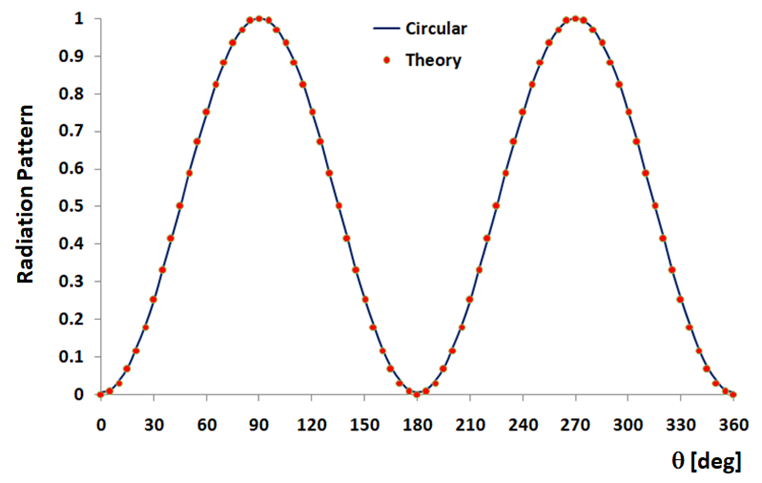
These calculated results and the comparison with the asymptotic expressions predicted by theory demonstrate the ability of AN-SOF to simulate small loop antennas.