Wave Matching Coefficient: Defining the Practical Near-Far Field Boundary

In this article, we explore the concepts of absolute wave impedance and wave matching coefficient (WMC) as practical alternatives to determine a useful boundary between the near and far field regions of an antenna. By utilizing these measures, we gain a better understanding of wave propagation as a function of distance from the source antenna, employing a decibel scale that enables clearer visualization of significant changes in wave impedance. As a general guideline, a WMC value of 20 dB proves to be an appropriate threshold for distinguishing between the near and far field zones. Through examples involving both elementary and large-scale antennas relative to the wavelength, we observe that the 20 dB boundary is consistently located at a distance of λ/3 for elementary antennas, while it takes on an irregular and non-spherical shape for antennas of comparable size or greater than the wavelength.

Introduction

The determination of the far-field region of an antenna has been a topic extensively discussed in books and texts on antennas for nearly a century. However, it continues to spark debates even today. Identifying the regions surrounding an antenna is crucial for various applications, such as near-field measurements in an anechoic chamber to predict the far-field radiation pattern or in electromagnetic compatibility (EMC) to optimize shielding in the near-field region, minimizing interference.

Based on the observation of elementary electric or magnetic dipole fields, three distinct regions can be identified in terms of the distance, r, from the dipole:

1) The reactive near-field region, where terms proportional to 1/r³ predominate.

2) A transition region or Fresnel zone, where terms proportional to 1/r² predominate.

3) The far-field region or Fraunhofer zone, where terms proportional to 1/r predominate.

There is also a two-region model where the reactive near-field and the Fresnel zone are considered as part of the same near-field region. When antennas are more complex than elementary dipoles, it becomes nontrivial to identify the electromagnetic field zones. It is important to note that the definition of a boundary between the near-field and far-field regions is always arbitrary and depends on the acceptable margin of error in practice. There is no sharp edge or discontinuity between these regions; instead, the electromagnetic field initially behaves as a quasi-static field near the radiation source and gradually transforms into a Transverse Electromagnetic (TEM) wave with a spherical wavefront as the distance increases.

The Traditional Boundary Between Near Field and Far Field

In most textbooks, we can find that the far-field region begins at a distance from the antenna given by 2D²/λ, where D is the maximum dimension of the antenna and λ is the wavelength. This boundary between regions works reasonably well for cases of electrically large antennas (D >> λ). However, there are many exceptions to this rule, such as in the case of parabolic antennas where this boundary must be extended twofold. For electrically small antennas (D << λ), the boundary between regions is located at λ/(2π) regardless of the antenna size.

These calculations are based on placing the observation point of the field far enough away so that the antenna remains within a sphere, which, as it expands, approaches a spherical wavefront in the far-field zone. This allows us to develop the phase of the Green’s function of the problem in a Taylor series with respect to distance and retain the first terms. Depending on the number of terms retained, the different field zones will be delimited. For an antenna that is large compared to the wavelength, if we move away to enclose it within a sphere, we may have already moved too far and find ourselves in the far-field region, missing the details of what happens in the near field and where a boundary between both zones could be defined. Hence, these analytical formulas fail in many cases.

Definitions of Wave Impedance

Instead of using a single formula for all cases, which introduces a high level of uncertainty, a more convenient criterion for separating the near-field and far-field regions is to calculate the so-called wave impedance, which is calculated as the ratio of the electric and magnetic fields. Since fields are vectors, we can compute the ratio between their components. For example, when a wave is vertically polarized, at the wavefront, we consider the vertical component of the electric field, E_v, and the horizontal component of the magnetic field, H_h, omitting components in the direction of propagation (which rapidly diminish with distance from the emission source). We define the wave impedance as Z_w = E_v/H_h. This ratio involves two complex quantities with real and imaginary parts, so the wave impedance has both magnitude and phase. By decomposing the wave at the wavefront into its right-handed circular polarization components, E_R and H_R, and left-handed circular polarization components, E_L and H_L, we can define two complex wave impedances: a right-handed impedance, Z_R = E_R/H_R, and a left-handed impedance, Z_L = E_L/H_L.

Regardless of the chosen definition of wave impedance, it will have the following properties:

• Z_w is a function of the distance from the antenna measured in wavelengths, r/λ, and the observation direction, given by two angles (zenith and azimuth) when using spherical coordinates.

• In any chosen direction, as the distance increases (r >> D and r >> λ), Z_w tends to 377 Ω in free space.

Therefore, in the far-field region, the wave impedance approaches the intrinsic impedance of the medium, which is 377 Ω for free space. For an ideal lossless and isotropic medium, the intrinsic impedance is given by Z_i = √(µ/ε), where µ is the magnetic permeability and ε is the dielectric constant. For vacuum, this value is approximately rounded to 377 Ω, often approximated as 120π Ω for convenience, with three significant digits.

Absolute Wave Impedance

The problem with defining wave impedance in terms of components of the E and H vector fields is that we have more than one definition, as we have just seen, and these definitions depend on the chosen coordinate system or frame of reference. A figure that allows us to identify the field regions should satisfy the following conditions:

• It should be calculated based on observables, i.e., quantities that can be measured in practice.

• It should be independent of the frame of reference, i.e., invariant under a coordinate transformation.

• It should be obtainable for any polarization of the field, even when it is unpolarized, as is the case when uncorrelated fields with random phases are summed.

A simple figure that meets these three requirements is what we will call the absolute wave impedance, which is given by the ratio of the root mean square (rms) values of the E(r) and H(r) vector fields,

Z_w(r) = E_rms(r)/H_rms(r), at each point r in space.

These are observables that are independent of the coordinate system. For example, when transforming from Cartesian to spherical coordinates, we have E_rms = |E| = √(|E_x|² + |E_y|² + |E_z|²) = √(|E_r|² + |E_Θ|² + |E_φ|²), where E_x, E_y, E_z, E_r, E_Θ, E_φ are complex components (if working with peak values, they should be multiplied by 1/√(2) to obtain rms values). The same applies to the rms value of the magnetic field, H_rms = |H|.

In general, E_rms and H_rms are invariant under any coordinate transformation. Therefore, Z_w(r) is defined at every point r in space outside the antenna surface because it is a quantity that can be calculated at any point r based on the measured fields, E_rms(r) and H_rms(r). Since this definition disregards the phase, it is also useful for unpolarized waves. Disregarding the phase of the wave impedance is not an issue since we will need to compare it with a real value, equal to 377 Ω (with zero phase), to determine if we are in the far-field zone.

Wave Matching Coefficient

Analogous to the definition of “return loss” used for transmission lines, if 377 Ω were the characteristic impedance of a line, we can define a coefficient in decibels that measures how well the wave impedance is “matched” to the intrinsic impedance of the medium. We will call this coefficient the Wave Matching Coefficient (WMC), given by

where Z_w = E_rms/H_rms is the absolute wave impedance. We will not use the term “return loss” because in the propagation mechanism we are considering, there is no loss or wave returning by reflection to the source that originated it.

As Z_w approaches 377 Ω, the WMC always increases. In a transmission line, a return loss of 20 dB implies that 99% of the power is transmitted and 1% is reflected. Although we don’t have a reflection mechanism here, we could adopt the same tolerance and consider the limit of WMC = 20 dB as the boundary between the near-field and far-field regions. If this limit proves to be too strict or too lenient for a particular practical application, we are free to choose another boundary according to the acceptable tolerance. From an engineering standpoint, we would recommend placing the boundary between the near-field and far-field regions above WMC = 10 dB. In the examples we will consider next, we will use the 20 dB boundary.

Examples with a 20 dB Boundary

Figure 1(a) shows the absolute wave impedance as a function of distance for an elementary electric dipole and an elementary magnetic dipole, while Figure 1(b) shows the corresponding WMC. The direction along which the distance r/λ varies is perpendicular to the axis of the dipoles, where the far-field reaches its maximum value. In both cases, the 20 dB boundary is practically at r/λ = 0.33 ≈ 1/3. Additionally, we could divide the near-field region into two parts, one below the maximum at r/λ = 0.1 and one above.

Figure 2(a) displays the absolute wave impedance for an elementary electric dipole along a direction at 45° from its axis, where the power density drops 3 dB compared to its maximum value, as well as the curve obtained in the previous Figure 1(a) along the direction at 90° from the dipole’s axis. Figure 2(b) shows the corresponding WMC. In this way, we observe the wave impedance and WMC for the directions that define the radiation maximum and the beamwidth of an elementary dipole.

We can observe that the boundary between the near-field and far-field regions moves away from the dipole when observed from a direction other than that of maximum radiation, and a transition zone opens around r/λ = 1/3.

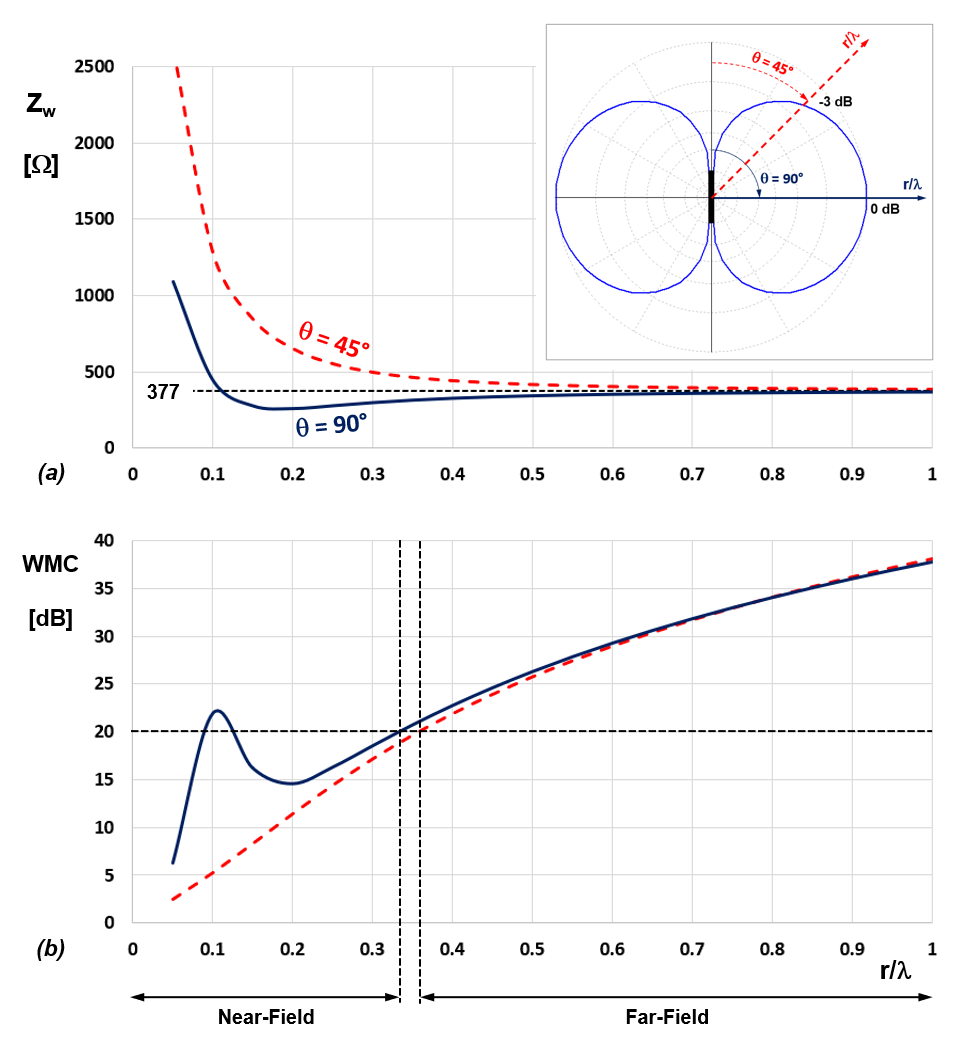
As an example of an antenna with a size of multiple wavelengths, Figure 3 presents the results for a 7-element Yagi-Uda antenna, optimized to provide maximum front-to-back ratio. Figure 3(a) shows the absolute wave impedance in the direction of maximum radiation, perpendicular to the antenna elements, and in the direction where the maximum power density drops by half (-3 dB) and defines the edge of the beamwidth. Figure 3(b) shows the corresponding WMC curves.

In this case, the 20 dB boundary also shifts to a greater distance when the observation direction is different from the direction of maximum radiation, similar to the elementary dipole. Additionally, the transition zone between the near-field and far-field zones is approximately half a wavelength.

We can see that the wave impedance can reach very high values, so representing the WMC provides a more convenient decibel scale for comparing large and small values.

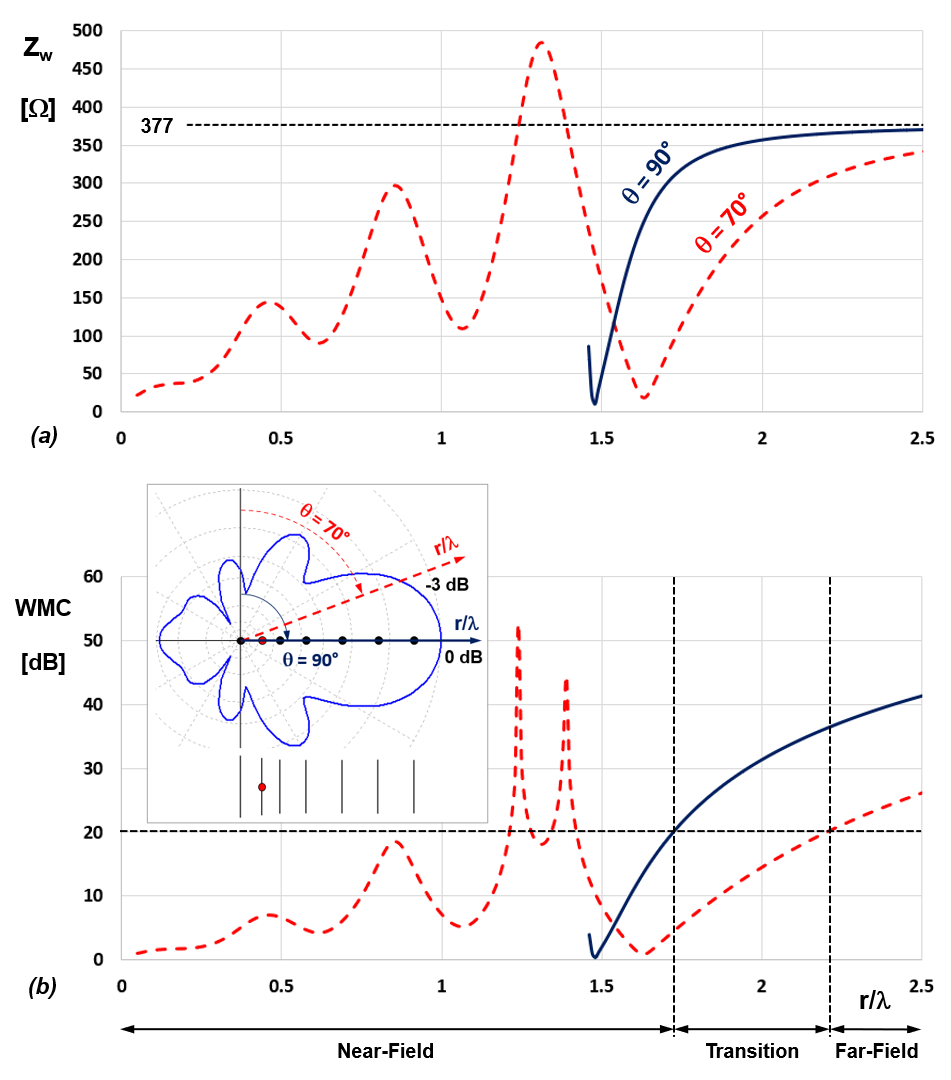
Another interesting example of a long-wavelength antenna is the axial mode helical antenna. Figure 4 shows the results for a left-handed helical antenna with a diameter of 0.3λ, a pitch of 0.22λ, and 10 turns, resulting in a total length of 2.2λ from end to end. The helix reflector, which is necessary for it to operate in axial mode (with maximum radiation along the helix axis), has a diameter of 0.95λ.

Figure 4(a) shows the wave impedance along the axis of the helix, from the base, passing through the interior of the helix until it exits. It also shows the wave impedance along a direction corresponding to the -3 dB beamwidth edge. Figure 4(b) shows the corresponding WMC results. Here, too, a displacement of the boundary between the near-field and far-field regions can be observed. However, in this case, the displacement is opposite to the previous cases since the field inside the helix is always “close.” We can see that as we traverse the interior of the helix along its axis, the boundary between the near and far-field zones begins at r/λ = 2.3, which is just a distance of 0.1λ above the top of the helix located at 2.2λ. This is logical since the interior of the helix behaves like a waveguide.

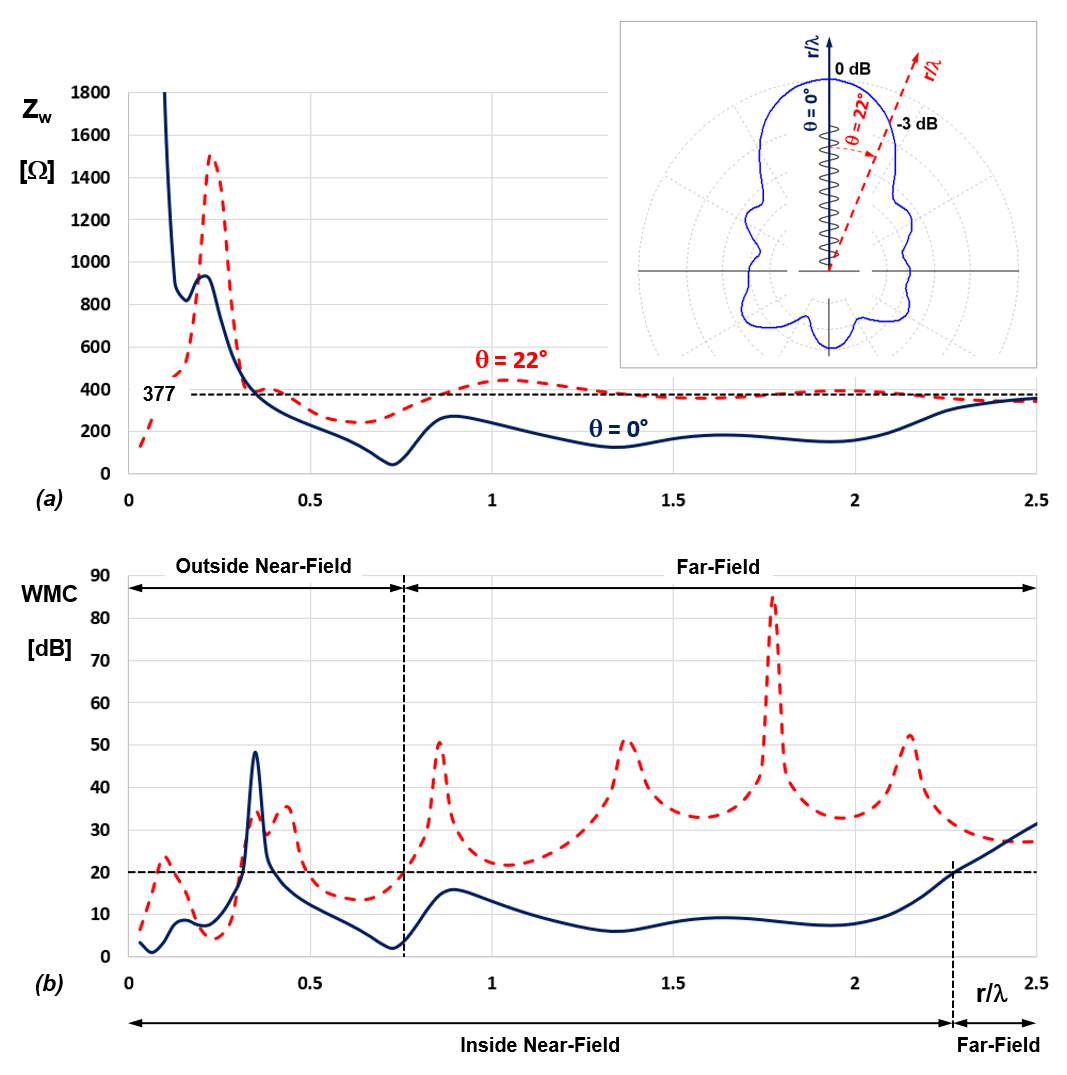
From these examples, we can deduce that the three-dimensional boundary between the near-field and far-field regions does not have a spherical or regular shape around antennas of a size comparable to or larger than the wavelength. The absolute wave impedance, and especially the WMC, allows us to determine where the far-field region begins in each direction of space. We could then choose the farthest boundary resulting from this analysis as the radius of a limiting sphere from which the far-field region begins in all directions.

Conclusions

In this article, we have presented the concepts of absolute wave impedance and Wave Matching Coefficient (WMC) as alternatives for determining a practical boundary between the near and far field regions of an antenna. The WMC, in particular, enables a better visualization of the evolving wave propagation as a function of distance from the originating antenna, providing a decibel scale that enhances the observation of significant variations in wave impedance. As a general guideline, we have observed that a WMC value of 20 dB defines an appropriate threshold for separating the near and far field zones.

Through examples involving elementary antennas and antennas of significant size relative to the wavelength, we have observed that the 20 dB boundary remains at a distance of λ/3 for elementary antennas. However, for antennas of comparable or larger size than the wavelength, the boundary assumes an irregular and non-spherical shape. In this particular case, the radius of a spherical boundary separating the near-field and far-field regions around the antenna will be determined by the maximum distance observed in all angular directions of space where the WMC reaches the 20 dB limit.

Further Reading

The traditional separation between field regions is explained in detail in section “4.4 Region Separation” of the renowned book “Antenna Theory, Analysis and Design” by Constantine A. Balanis, 4th edition, 2016, John Wiley & Sons. For a compelling analysis utilizing wave impedance, refer to “Near Field or Far Field?” by Charles Capps, EDN, Design Feature, Aug. 16, 2001, pp. 95-102. A comprehensive examination can also be found in the paper “Where Does the Far Field of an Antenna Start?” by M. Abdallah, T. Sarkar, M. Salazar-Palma, and V. Monebhurrun, published in IEEE Antennas & Propagation, Vol. 58, Issue 5, Oct. 2016, pp. 115-124.