Defining the Environment

Ground Plane Options

Navigate to the Setup tab in the main window and access the Environment panel. You can adjust the relative permittivity and permeability of the surrounding medium within the Medium box, as shown in Fig. 1.

There are four ground plane options available:

None

When the None ground plane is selected, the simulation will be conducted in free space, with the relative permittivity and permeability values set in the Medium box (see Fig. 1).

Perfect

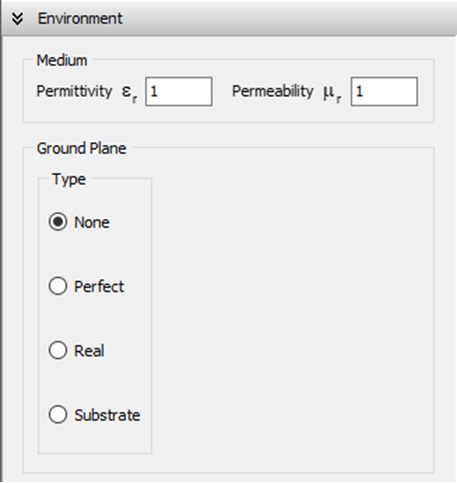
An infinitely large perfectly electrically conducting (PEC) ground plane will be positioned at the specified height from the xy-plane (“Z Position” in Fig. 2). Consequently, the ground plane will be parallel to the xy-plane. The “Z” position determines the height of the ground plane above the xy-plane, with a negative Z indicating placement below the xy-plane.

When the Perfect option is selected, all wires must be positioned above the perfect ground plane. In simpler terms, all wires must have a Z-coordinate greater than or equal to the specified position. AN-SOF does not verify wires for potential crossings with the PEC ground plane or for placement at the bottom of the plane. Additionally, it does not support horizontal wires lying directly on the ground plane. However, it does allow for connections to be established from wire ends to the ground plane.

Real

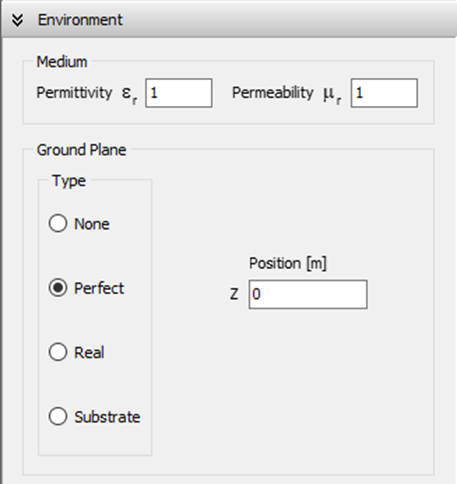
A real ground plane, with user-defined conductivity and relative permittivity (relative permeability set to 1), will be situated on the xy-plane at z = 0, as shown in Fig. 3. There are three available options for real ground calculations: Sommerfeld-Wait/Asymptotic, Reflection Coefficients/Asymptotic, and Radial wire ground screen.

All wires must be positioned above the ground plane (z = 0). Horizontal wires placed directly on the ground plane are not supported. However, wire end connections to the ground plane can be established when either the “Sommerfeld-Wait/Asymptotic” or “Radial wire ground screen” options are selected.

The “Reflection Coefficients/Asymptotic” option exclusively permits connections to the ground plane for vertical wires, resulting in perfect zero-Ohm connections. In cases involving horizontal wires, they must be separated by at least one free space wavelength from the ground plane. In such situations, it is essential to verify the validity of the results. AN-SOF does not automatically verify whether these conditions are satisfied within a model.

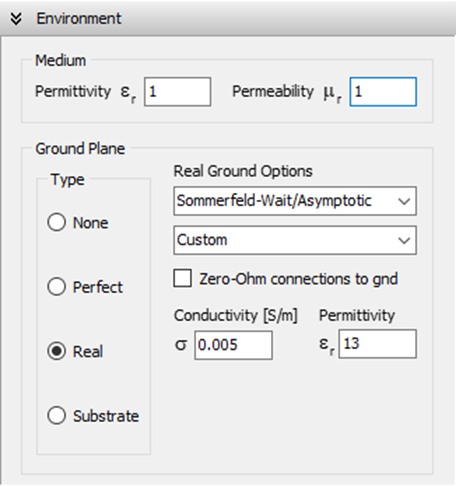
Real Ground Options

Sommerfeld-Wait/Asymptotic

This option involves calculating the currents flowing through the antenna/wire structure using a model that includes a perfect ground plane and incorporates equivalent loss impedances to address power dissipation in the ground plane, particularly when wires are in close proximity to or connected to the ground. Developed by Prof. James R. Wait, this model is particularly effective for obtaining the input impedance of low-frequency (LF) and medium-frequency (MF) antennas, especially in scenarios where the ground conductivity is high within those frequency bands. Additionally, the finite conductivity and permittivity of the ground are employed to calculate the near-field and far-field radiation from the structure, utilizing the Sommerfeld-Norton asymptotic expressions and Fresnel’s reflection coefficients, respectively.

Connections to the ground are permitted, either at the start or end point of a wire with z = 0, and they are considered imperfect by default. This means that currents flowing between the ground and the grounded wires result in power losses in the ground. However, if you select the “Zero-Ohm connections to ground” option, wire connections to the ground will be treated as perfect, with no power dissipation occurring at the connection point.

Reflection Coefficients/Asymptotic

In this option, the ground parameters have an impact on the current distribution on the antenna or wire structure above the ground. This influence is determined through a generalization of Fresnel’s reflection coefficients, which means that the input impedance of a transmitting antenna is also influenced by the real ground conditions. Moreover, the near and far fields are affected by the finite ground conductivity and its dielectric constant. The near fields are computed using the Sommerfeld-Norton asymptotic expressions, allowing us to calculate the electric and magnetic field as a function of distance from the transmitting antenna. This enables us to observe the attenuation resulting from ground losses. The far-field, on the other hand, is computed using standard Fresnel’s reflection coefficients.

Vertical wire connections to the ground are permitted, but they are treated as lossless connections.

Radial wire ground screen

In this option, a ground screen consisting of buried radial wires will be positioned beneath the ground plane. The screen is centered at the origin of coordinates and features user-specified parameters, including the number of radial wires, wire length (or radius of the circular screen), and wire radius.

The ground screen model influences the current distribution on the antenna/wire structure by calculating the power dissipated in the ground plane-wire screen system. Consequently, the presence of the screen and the finite ground conductivity will impact the input impedance of a transmitting antenna located above the ground screen. Additionally, the finite ground conductivity and permittivity are employed to compute the near- and far-fields radiated from the structure, utilizing the Sommerfeld-Norton expressions and the Fresnel’s reflection coefficients, respectively.

Connections to the ground are permitted, either at the start or end point of a wire with z = 0, and they are considered imperfect by default. This means that currents flowing between the ground and the grounded wires result in power losses in the ground. However, if you select the “Zero-Ohm connections to ground” option, wire connections to the ground will be treated as perfect, with no power dissipation occurring at the connection point.

Substrate

A dielectric substrate, with a user-defined permittivity, will be positioned beneath the xy-plane (z = 0), as shown in Fig. 4. The substrate can either extend infinitely or have finite dimensions in the xy-plane. It is essential to specify the slab thickness, denoted as ‘h,’ along the z-axis. A perfectly electrically conducting (PEC) ground plane will be situated at z = -h, just below the dielectric slab, as illustrated in Fig. 5. To facilitate setting the substrate’s permittivity, choose from a drop-down list with common materials (e.g., FR4, RT/Duroid, Rogers RO slabs).

When the Substrate option is selected, all wires must be positioned on the xy-plane (z = 0). These wires can represent flat traces of planar or patch antennas printed on the dielectric substrate, microstrip lines, or PCB (Printed Circuit Board) traces. The only exception to this rule is for vertical wires, which can be employed to connect wire strips at z = 0 to the PEC ground plane at z = -h. Typically, a voltage or current source is connected to these vertical wires to power the system, whether it’s an antenna or a PCB.

It’s important to note that the PEC ground plane beneath the dielectric substrate cannot be omitted from the model, meaning that ungrounded substrates are not supported with this option. Wires positioned above the xy-plane (with z-coordinates > 0) or below the PEC ground plane of the substrate (with z-coordinates < -h) are not supported. AN-SOF does not automatically verify compliance with these conditions.