Gain of Helix in Normal Mode

Created OnOctober 31, 2022

Updated OnMay 15, 2023

By:Tony Golden

Helical Geometry

The current distribution in a helical antenna of arbitrary size cannot be described in terms of simple series or elementary functions, so most of the available data has been obtained experimentally. The helical antenna was invented by Prof. John Krauss who has investigated its performance as a function of geometry extensively. Refer to “Antennas” by John D. Krauss, 2nd Edition, McGraw-Hill, 1988.

The helix has basically two modes of operation,

The normal mode or broadside mode where the maximum radiation occurs in the plane normal to the helix axis.
The axial mode or end-fire mode where the maximum radiation occurs along the helix axis.

The normal mode is obtained in helices that are small compared to the wavelength, therefore their behavior is similar to that of a small loop > with the same number of turns as the helix and with a uniform current distribution. This can be considered as a limiting case and the simulation results can be compared with theory. When the helix size is comparable to the wavelength, the current distribution can no longer be considered uniform and the simulation results will be only compared with measurements.

The helix geometry is usually described in terms of its circumference normalized to the wavelength, C/λ (C = 2πR, R being the helix radius), number of turns, N, and pitch angle, α, defined as

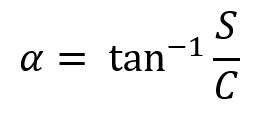
S being the pitch or spacing between turns. The starting point and the axis direction of the helix can also be set in AN-SOF, as Fig. 1 shows.

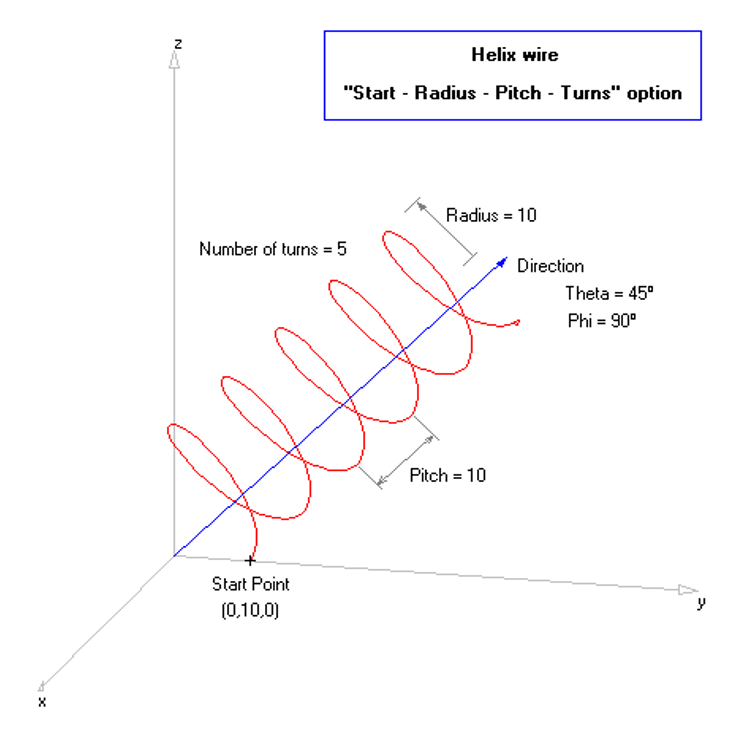
*Fig. 1: Helix drawn using the “Start – Radius – Pitch – Turns” option in AN-SOF.*

In the simulations that follow the helix axis will be the z-axis. Also, a ground plane will be placed at z = 0, so the starting point of the helix will be (0,0,Zs), with Zs being small compared to the wavelength. The helix will be connected to the ground plane by means of a short wire having one segment, where a voltage source will be placed.

Normal Mode

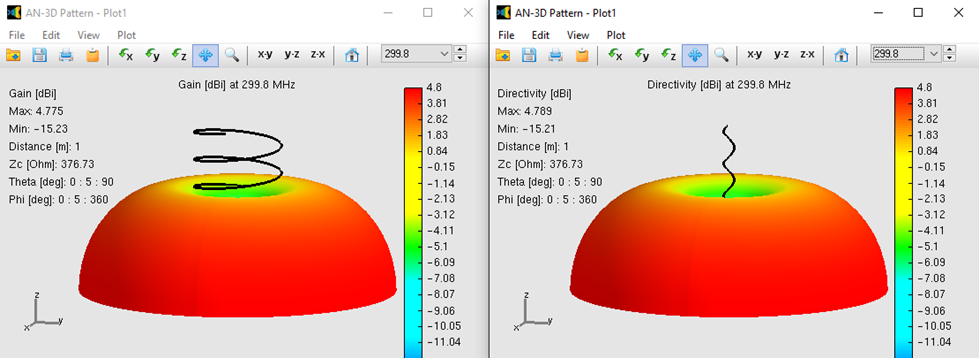
For the normal mode of operation, an small helix having a circumference C/λ = 0.01, 5 turns and a variable pitch will be simulated. The pitch varies between 0.001λ and 0.01λ. For these small dimensions, the theoretical prediction is that the radiation pattern must be doughnut-shaped as that of a small loop, with a null along the helix axis. Moreover, the gain in the presence of a perfect ground plane must be 3 (dimensionless) or 4.77 dBi.

Fig. 2 shows the computed 3D radiation patterns of the small helix for a pitch of 0.001λ (left) and 0.01λ (right). It can be seen that the results correspond to the theoretical predictions. The small departure from 4.77 dBi obtained for the largest pitch must be interpreted as a deviation from the theoretical limiting case of an infinitely small helix. This behavior can be appreciated if we plot the peak gain as a function of the pitch, as in Fig. 3, where we can see that the computed gain tends to 4.77 dBi as the pitch tends to zero.

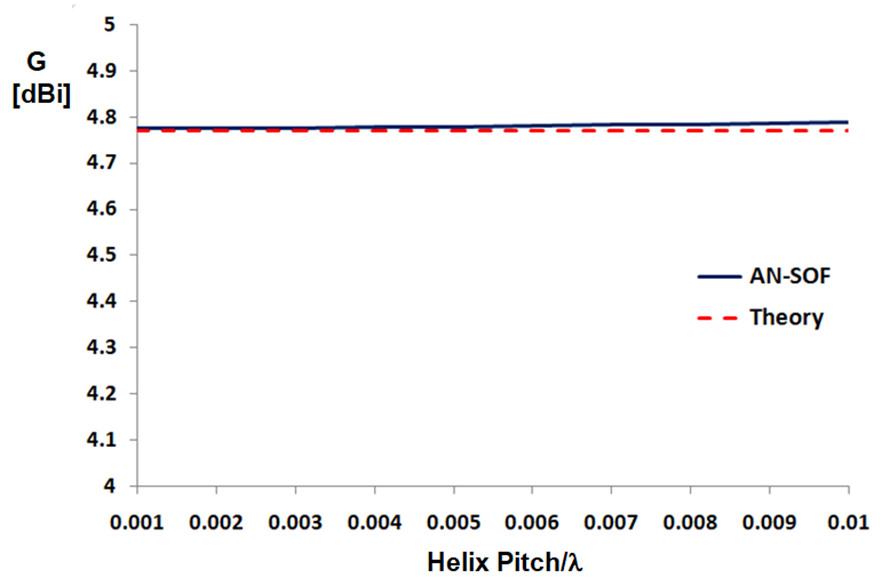
*Fig. 2: Gain pattern in dBi of a small helix above a perfect ground plane for C/λ = 0.01, 5 turns, pitch = 0.001λ (left) and pitch = 0.01λ (right).*

*Fig. 3: Gain of a small helix above a perfect ground plane as a function of the pitch for C/λ = 0.01, 5 turns.*

This result demonstrates the ability of AN-SOF to simulate curved structures with a small size compared to the wavelength.