Search for answers or browse our Knowledge Base.
Guides | Models | Validation | Blog
The Conformal Method of Moments
Introduction
The Method of Moments (MoM) is widely recognized as one of the most reliable techniques for modeling and simulating antennas and radiating systems. However, traditional implementations of MoM suffer from several issues primarily stemming from approximations used in numerical calculations to reduce computational requirements. While these approximations were justified in the 1970s and 1980s due to limited processor speeds and memory capacities, the present-day computing power, even on personal computers, allows for more accurate calculations. The limitations imposed by these approximations in traditional MoM models restrict their validity and applicability.
The fundamental principle of MoM involves representing metal surfaces through wire segments, which is a suitable approximation for many metallic antennas, particularly wire-type antennas like linear antennas, dipoles, monopoles, yagis, log-periodic arrays, quads, antenna arrays of all types, traveling wave antennas, fractals, aperture antennas, and reflectors. It is essential for each wire segment to have a small length and cross-section relative to the wavelength. The MoM seeks to determine the unknown current flowing through each wire segment, as depicted in Fig. 1.
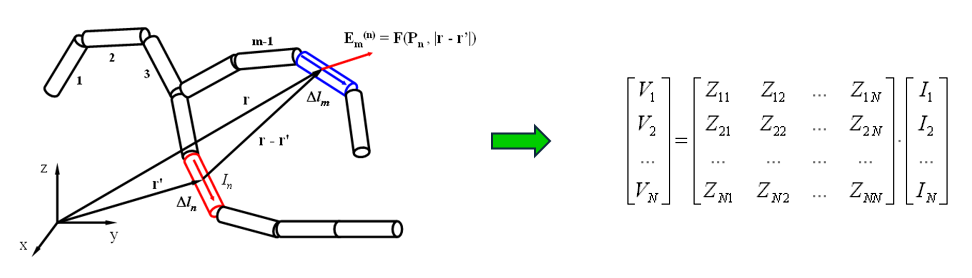
The Thin-Wire Approximation
In the modeling of antennas using cylindrical wire segments, the initial approximation commonly employed is known as the “thin-wire approximation,” as illustrated in Fig. 2. This approximation is based on the following assumptions:
- The electric current flowing through a wire can be represented as a filament along the wire axis, disregarding the fact that it actually flows on the wire’s surface.
- Variations in the current along the circular contour of the wire’s cross-section can be ignored.
- The component of the current perpendicular to the wire axis can be disregarded.
- It is sufficient to enforce the boundary condition of zero total tangential electric field on the surface of an ideal conducting wire along its axis.
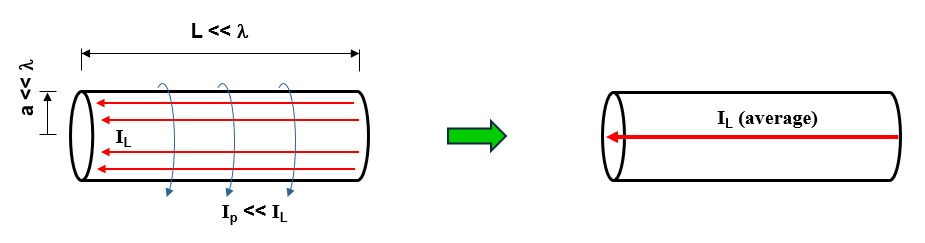
When dealing with a wire segment with a cross-section significantly smaller than the wavelength, assumptions 2, 3, and 4 are reasonably valid and align with experimental observations and theoretical predictions in the quasi-electrostatic regime for metal surfaces. However, assumption 1, regarding the current filament along the wire axis, has sparked debates throughout the history of linear antennas.
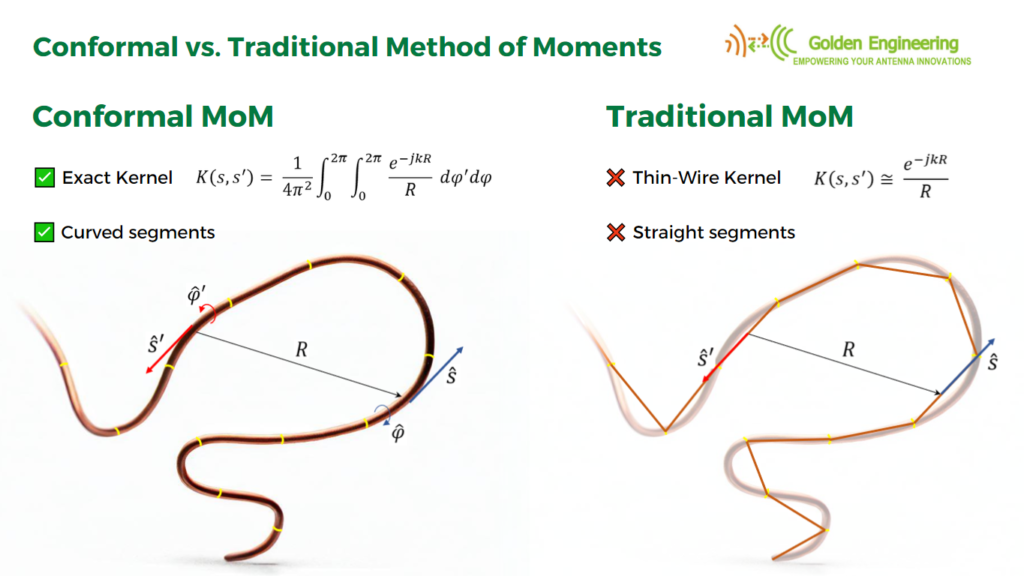
Assumption 1 only holds as a limiting case when the wire’s cross-section approaches zero size, such as when the wire has a circular cross-section and its radius tends to zero. This assumption relates to the crucial aspect known as the Kernel of the problem. The Kernel represents the core of the integral equation that the MoM solves to determine the currents flowing along the wires. Instead of employing the “thin-wire Kernel” utilized in traditional MoM, which is based on assumption 1, AN-SOF employs the exact Kernel. In the exact Kernel, it is considered that the current flows on the surface of the wires rather than being confined to a filament along the wire axis.
Eliminating assumption 1 has a significant impact on the accuracy of calculations, particularly in the current distribution near the antenna’s feed point or terminals, where obtaining precise values for input impedance and standing wave ratio (SWR) is crucial. In addition to discarding assumption 1 in AN-SOF, the use of the exact Kernel and curved wire segments helps overcome other issues inherent in traditional MoM, as described below.
Overcoming the 7 Limitations of the Traditional MoM
In AN-SOF, we have departed from the traditional MoM and embraced innovation by implementing a new method called the Conformal Method of Moments (CMoM) with an exact Kernel formulation. This decision stems from the lack of substantial improvements in traditional methods over several decades, despite advancements in computational power. By adopting CMoM with an exact Kernel, we have successfully addressed the main limitations of the traditional MoM, which can be categorized into seven key areas:
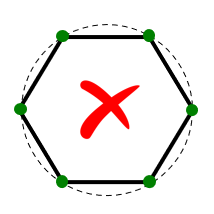
1. No curved wires:
Traditional MoM models rely on straight wire segments, which are suitable for linear antennas such as dipoles and their arrays. However, many antennas and structures have curved shapes. In traditional MoM, curved wires are approximated using a series of straight-line segments, leading to modeling errors that persist throughout the simulation. This approximation often produces inaccurate results for curved antennas like loops, helices, and spirals, particularly in terms of feed point impedances.
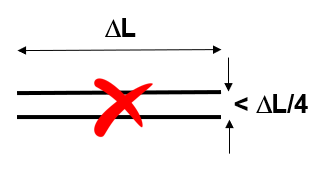
2. Wire spacing limitation:
Another limitation of traditional MoM is the spacing between parallel wires. Misleading results occur when the spacing between segments is less than a quarter of the segment length. As a result, the traditional MoM becomes less applicable when modeling configurations with close parallel wires, such as in two-wire transmission lines.
3. Issues with bent wires:
The thin-wire Kernel employed in traditional MoM leads to erratic numerical oscillations when wires are bent at right angles or have angles less than 30 degrees between adjacent segments.
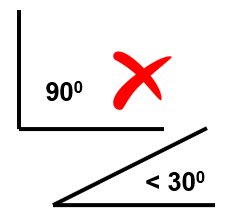
4. Short segment constraint:
Traditional MoM imposes a constraint on the segment length, requiring it to be greater than 0.001 of a wavelength. Consequently, the traditional MoM cannot be effectively applied at very low frequencies. For instance, when modeling an electric circuit of around 1 meter operating at 60 Hz, the segment length needed to accurately represent the circuit becomes at least 5,000 times shorter than the minimum segment length supported by traditional MoM. Therefore, the traditional MoM implementation falls short when modeling wire antennas at low frequencies.
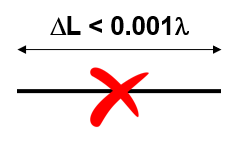
5. Thin wire requirement:
Thick wires deviate from the thin-wire approximation assumption, where current flow is limited to the wire axis rather than its surface. This deviation introduces significant errors in the results.
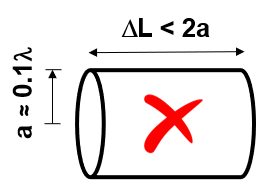
6. Tapered wire issues:
Changes in radius between adjacent segments create non-physical discontinuities in traditional MoM simulations.
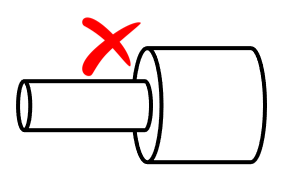
7. Proximity to lossy ground plane affects horizontal wires:
Antennas such as monopoles positioned above ground screens with elevated radial wires exhibit diverging input impedance and inaccurate antenna efficiency due to the influence of the lossy ground plane.
Thanks to the Conformal Method of Moments (CMoM) with Exact Kernel, AN-SOF has successfully eliminated these limitations. CMoM employs conformal segments that accurately capture the structure’s contour, enabling an exact representation of geometric details. Conformal segments, resembling curved cylindrical tubes, enable precise modeling of curved wires. By employing the exact Kernel instead of the thin-wire approximation, AN-SOF overcomes limitations associated with bent wires, small wire spacings, and segment lengths. This approach facilitates highly accurate calculations compared to the traditional method.
With the implementation of CMoM and an exact Kernel formulation, AN-SOF achieves enhanced accuracy, reduced computational requirements, and more efficient simulations. The improved method enables AN-SOF to simulate a wide frequency range, spanning from extremely low frequencies (e.g., 60 Hz circuits) to microwave antennas.
AN-SOF stands as the only antenna modeling software that offers a calculation engine based on the Conformal Method of Moments with an Exact Kernel.
