Linear Antenna Theory: Historical Approximations and Numerical Validation

Created OnJune 1, 2023

Updated OnOctober 18, 2024

By:Tony Golden

Discover the vital role of historical theoretical results alongside advanced numerical calculations in accurately approximating current distribution on linear antennas.

Simulation results depicting the input impedance of a center-fed half-wave dipole as a function of its length-to-radius ratio.

This article provides a comprehensive review of the theoretical approximations to the current distribution on linear antennas that were analytically derived during the first half of the 20th century. While the advancements in computing and numerical calculation methods have enabled higher precision, the historical theoretical results continue to serve as vital references for validating calculation methods implemented in algorithms. By examining these approximations, researchers can ensure the accuracy and reliability of modern numerical techniques used in antenna analysis and design.

Historical Theoretical Results: Approximations to Current Distribution

In 1956, Ronold W. P. King published his monumental work titled “The Theory of Linear Antennas,” which laid the foundation for understanding linear antennas and became a benchmark for future research. This section explores the significant contributions of King’s work, specifically focusing on the first four approximations to the current distribution on cylindrical antennas derived through an iterative method.

0th-Order Approximation > Perfect Sinusoid for Infinitely Thin Antennas: The 0th-order approximation considers infinitely thin antennas (wire radius = 0) with a delta-gap source (zero gap width between the antenna terminals at the source position). This approximation involves a perfect sinusoidal current distribution.

1st-Order Approximation > Accounting for Finite Radius Effect: The 1st-order approximation incorporates the finite radius effect (wire radius > 0) into the current distribution calculation. In this case, it is necessary to incorporate an additional term to the perfect sinusoidal function in order to obtain the 1st-order current distribution.

2nd-Order Approximation > Controversies Surrounding Finite Gap at the Source: The 2nd-order approximation takes into account the finite gap at the source position, which has historically sparked controversies and debates.

3rd-Order Approximation > Considering Feedline Effect: The 3rd-order approximation considers the feedline effect, which accounts for the boundary conditions at the feeding point resulting from the connection of a transmission line to feed the antenna.

Current Distribution Along a Half-Wave Dipole

To illustrate the aforementioned approximations, this section focuses on the current distribution in amplitude along a center-fed half-wave dipole. Figure 1 provides a graphical representation of the normalized current, i(s), as a function of position in wavelengths, s/λ. It should be noted that the actual current distribution exhibits a sign change in its derivative, ∂i/∂s (the electric charge), at the dipole center due to the excitation source.

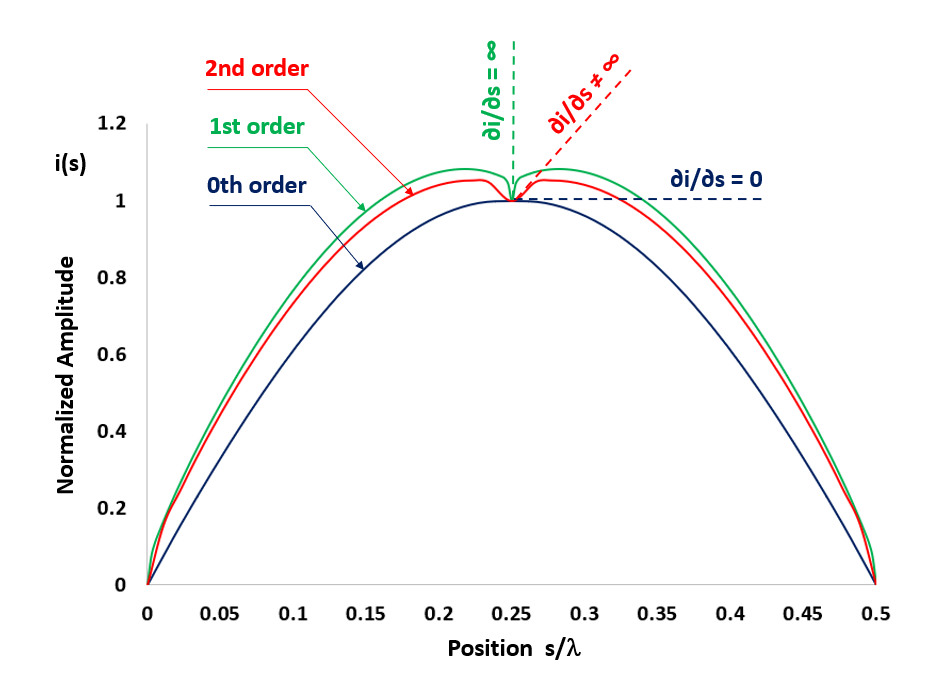
Fig. 1: Normalized amplitude current distribution along a center-fed half-wave dipole. The figure illustrates the 0th, 1st, and 2nd order approximations, highlighting the discontinuity of the current derivative at the feed point.

0th-Order Approximation > Perfect Sine Function with Zero Derivative: Figure 1 demonstrates that the 0th-order approximation, representing a wire radius of 0, yields a perfect sine function. Consequently, the derivative at the source position is zero, ∂i/∂s = 0. However, King’s analytical solution results in a finite input impedance of 73.1 + j42.5 Ω, which has been widely accepted and corroborated by other methods.

1st-Order Approximation > Finite Wire Radius and Divergent Input Impedance: The 1st-order approximation considers a finite wire radius and exhibits an infinite derivative, ∂i/∂s = ∞, at the source position. This singularity arises from the zero gap at the antenna terminals and has generated extensive debates throughout the history of linear antennas. As a consequence, the input impedance diverges.

2nd-Order Approximation > Finite Source Gap and Converging Input Impedance: Incorporating a finite source gap, the 2nd-order approximation yields a finite derivative at the source position. As a result, the input impedance converges to a finite value, dependent on the dipole wire thickness and the separation between its feeding terminals.

3rd-Order Approximation > Consideration of Transmission Line Feed: Although not visually distinguishable from the 2nd order on a graph, the 3rd-order approximation accounts for the characteristic impedance of the transmission line at the feed point. This effect, though small, can be accurately calculated using the Method of Moments with an exact Kernel.

Validating Numerical Methods: Impedance Convergence

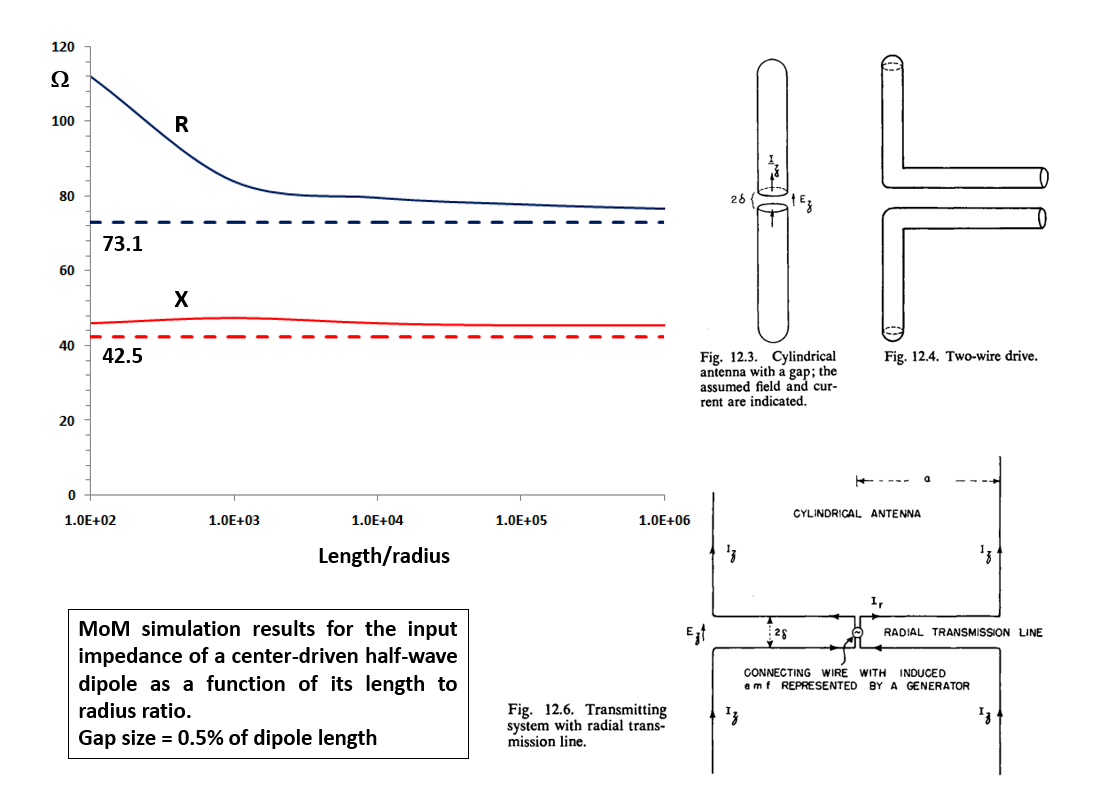
Validating numerical methods is a critical step in ensuring their accuracy, achieved by examining the limiting cases predicted by theory. As demonstrated, the 0th-order input impedance (wire radius = 0) of a center-fed half-wave dipole is determined to be 73.1 + j42.5 Ω. Consequently, this value should serve as a horizontal asymptote for the input impedance when the dipole length-to-radius ratio tends to infinity.

Figure 2 presents simulation results obtained using AN-SOF, which utilizes the Method of Moments with an exact Kernel. The figures from King’s book illustrate the antenna terminals in detail, where a radial transmission line was considered to account for 3rd-order effects. Notably, the calculated input impedance indeed converges to the theoretical value as predicted.

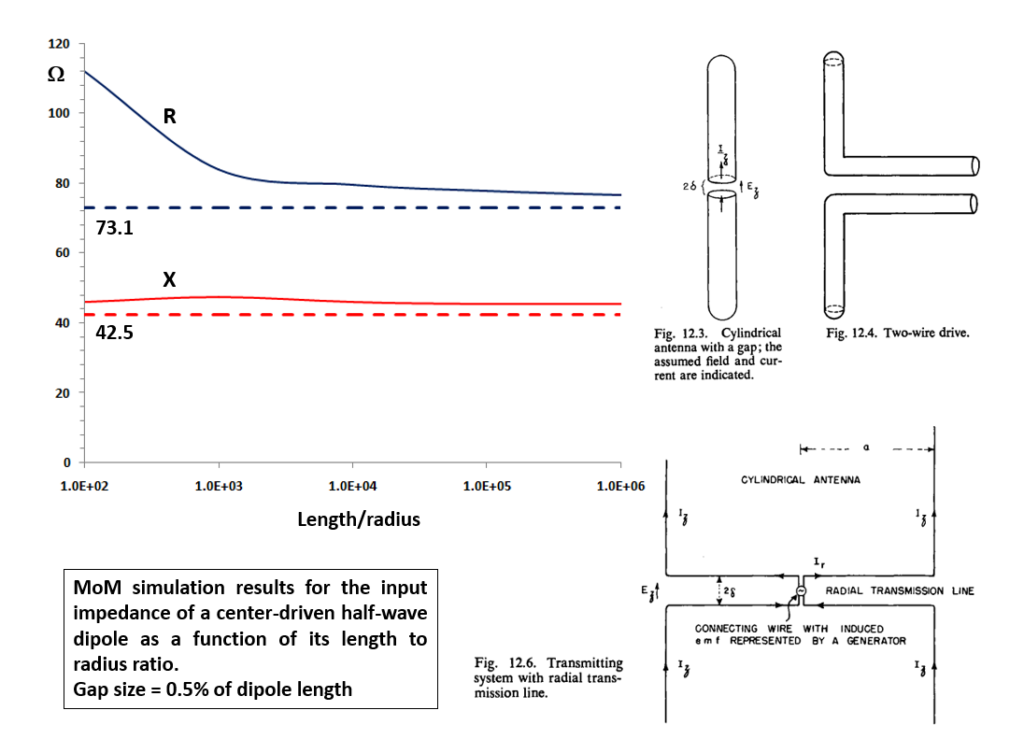
For a more comprehensive investigation into the impedance convergence of cylindrical antennas, a detailed study on the validation of AN-SOF can be accessed through this link.

Conclusions

This article has reviewed the historical approximations of current distribution on linear antennas as presented in Ronold W. P. King’s book. The four approximations, namely the 0th, 1st, 2nd, and 3rd-order approximations, have been thoroughly examined. These approximations progressively refine the theoretical model of a cylindrical antenna by considering factors such as the finite wire radius, the finite gap at the feed point, and the incorporation of the connected transmission line.

Moreover, the article has highlighted the importance of numerical validation in establishing the reliability of modern methods. The validation process involved comparing the numerical results to the limiting cases predicted by theory. Through the AN-SOF simulation, which utilizes the Method of Moments with an exact kernel, the calculated input impedance successfully demonstrated convergence to the theoretical values.