Convergence of the Dipole Input Impedance

One of the validation checks consists of incrementing the number of segments as the antenna length, radius and source gap remain constant. In this way, the input impedance should converge to an asymptotic value as the number of segments increases.

Fig. 1 shows the input impedance of a center-fed dipole antenna as a function of the number of segments, N, in each antenna arm for different half-lengths, h/λ, and for two radii, a/λ = 0.001191 (3/32″ at λ = 1 m) and a/λ = 0.009525 (3/4″ at λ = 1 m). The input impedance of a short (h/λ = 0.175), half-wave (h/λ = 0.25) and full-wave (h/λ = 0.5) dipole antenna is shown.

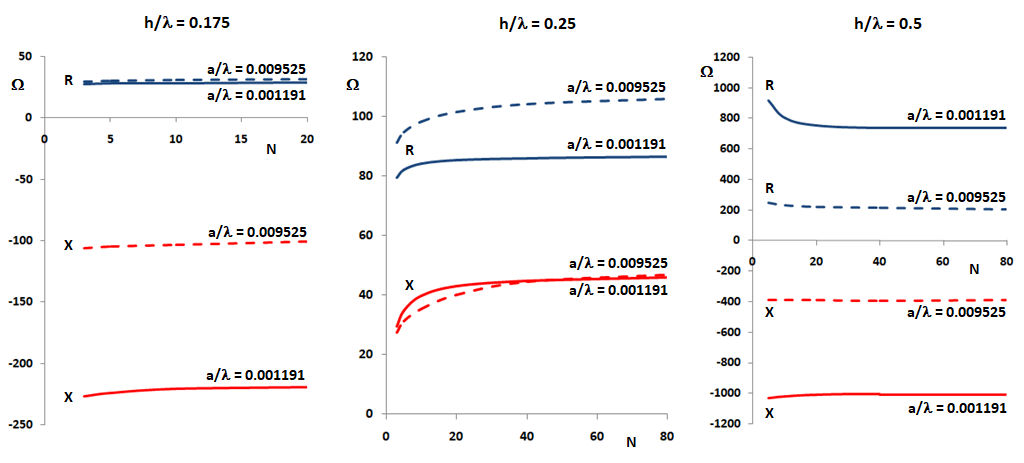
The input resistance, R, and reactance, X, converge quickly and monotonically in all cases. However, the convergence is a bit slower in the case of the half-wave dipole when it is relatively thick (a/λ = 0.009525). In practice, these curves show us that if we take 20 segments per wavelength along a linear antenna, then the input impedance will differ about 5% of its asymptotic value. Even taking 10 segments per wavelength the error will be 10% to 15%, which is good enough as a first approximation.

We can also investigate the convergence behavior of the input impedance of a center-fed cylindrical antenna of fixed dimensions as a function of frequency.

Fig. 2 shows the input resistance and reactance spectrum of a dipole having a length of 0.5 m, a radius of 5 mm and a gap at the source position of 0.02 m. The frequency is varied from 100 to 1500 MHz, so the wavelength goes from 0.2 m to 3 m. Therefore, the normalized antenna dimensions vary in the following ranges: 0.167λ < length < 2.5λ, 0.00167λ < radius < 0.025λ, 0.00667λ < gap < 0.1λ. Three curves have been obtained for a number of segments in each antenna arm of N = 5, 10 and 20.

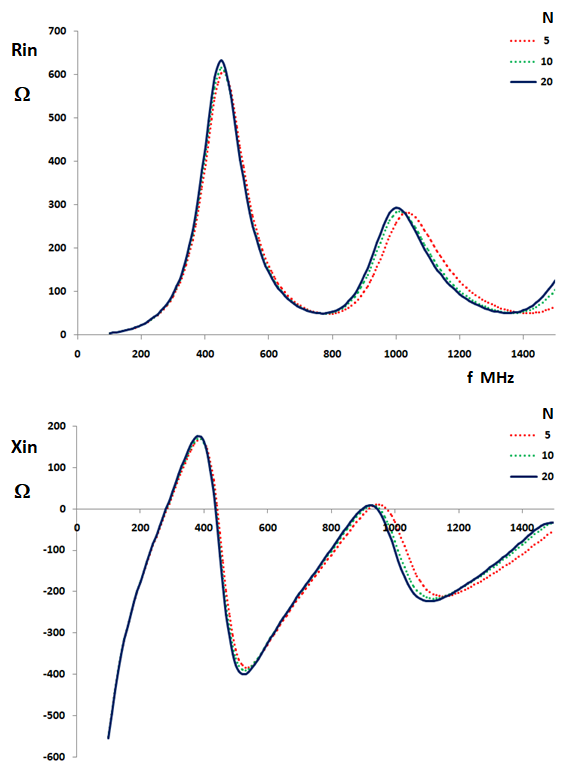
We can see that the input impedance curves converge towards a single curve as the number of segments is increased. Besides, the difference between the curves for N = 10 and N = 20 is small even for a frequency as high as 1200 MHz, which means a wavelength of λ = 0.25 m and a dipole length of 2λ.

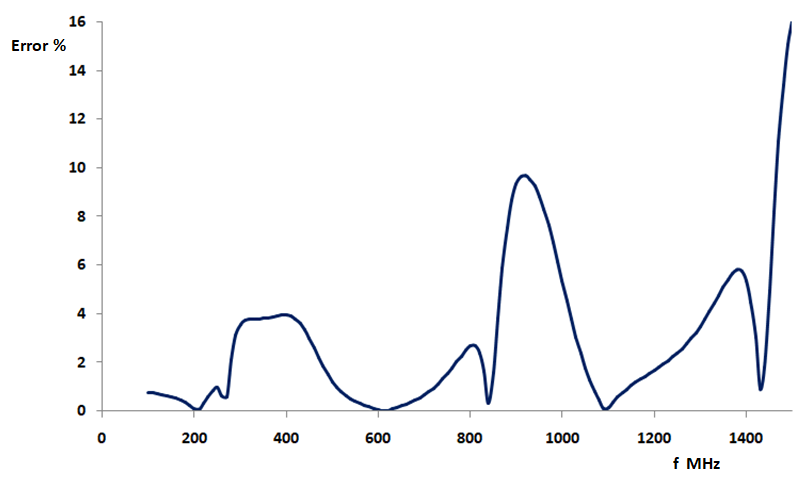
This result reinforces the previous estimation of choosing 10 segments per wavelength (2N/(2λ) for N = 10) to obtain a practically useful value for the input impedance. In Fig. 3 the percentage difference between the absolute values of the input impedance for N = 10 and N = 20 is shown. This error is well below 5% in most of the frequency range analyzed. Only near the third resonance at about 900 MHz the error rises up to 10%. Also, we can see that the useful bandwidth to use 10 segments per wavelength goes even to 1450 MHz or λ = 0.207 m, which gives us a dipole length of 0.5m/0.207m = 2.4λ. This means that we could even use 8 segments per wavelength (2N/(2.4λ) for N = 10).

It is interesting to compare the convergence of the AN-SOF results with those obtained from the NEC-2 engine. In Fig. 4 the input impedance of a center-fed half-wave dipole is shown as a function of the number of segments, N, in each dipole arm. The dipole radius is 0.005λ and the source gap is 0.025λ. We can see that the results obtained from AN-SOF converge monotonically while the NEC results diverge.

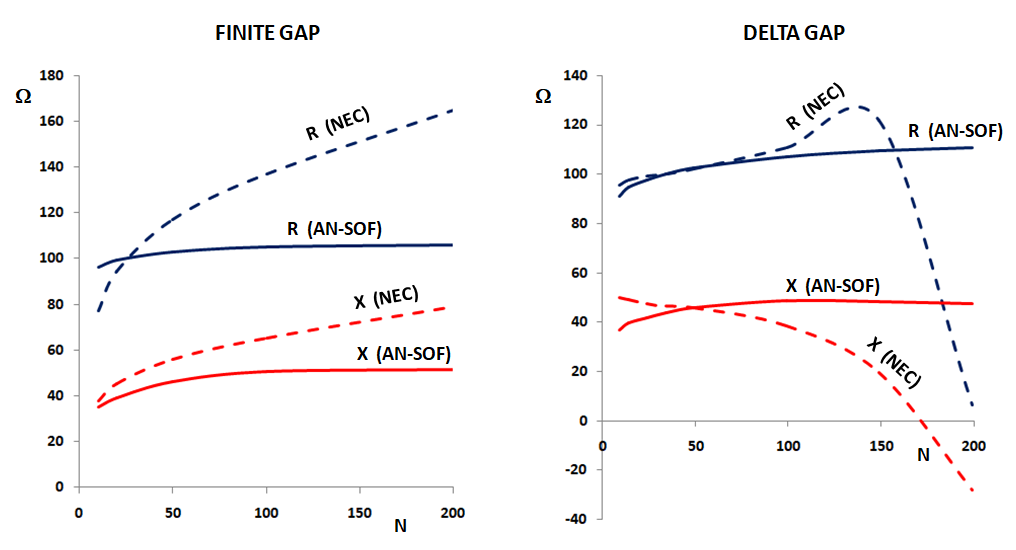
The divergence shown in the NEC impedance is due to two causes, viz. First, as the number of segments grows, so does the difference between the lengths of the segments adjacent to the source gap and the width of the gap. Because the gap is filled with another segment, we have segments of different lengths that are connected to each other. This is a situation that NEC is not well prepared to deal with, as it is well known that connected and adjacent segments must have similar lengths in NEC. Second, as the number of segments increases, each segment becomes thicker and thicker (with increasing radius-to-length ratio) and in NEC only an extended kernel has been implemented to handle thick wires, not the “exact” kernel.

The kernel is the heart of the integral equation that is solved numerically using the Method of Moments (MoM) > to calculate the current distribution. In old implementations of the MoM it is common that a thin-wire approximation to the kernel or an extended version has been used. Neither of these two NEC problems occurs in AN-SOF, since adjacent segments can have any length and also any radius-to-length ratio, because the exact kernel has been implemented instead of an approximation of it (there is a practical limitation, of course, where the rounding errors begin to predominate, but this is a limit hardly achievable by any simulation in practice).

The results for a delta-gap source are also shown in Fig. 4. In the delta-gap case the gap width tends to zero, so the segment at the source position also decreases its length as the number of segments increases. It is well known that the input impedance diverges as the number of segments increases when a delta-gap source is used. However, it is worth doing the exercise of calculating the input impedance in this case to observe the stability of the numerical results. We can see that the AN-SOF results are stable and grow monotonically (we could even say that the reactance almost converges) unlike the NEC results.

Going back to theory, there is a well-known limiting case for the input impedance of a half-wave dipole, namely, it is 73.1 + j 42.5 Ohm for an infinitely thin antenna. Therefore, these values will be horizontal asymptotes of the impedance as a function of the length/radius ratio when the radius tends to zero. In Fig. 5 the AN-SOF results are shown as well as the theoretical asymptotes. The source gap used is 0.0025λ, but the input impedance becomes independent of the gap width as the length-to-radius ratio increases.

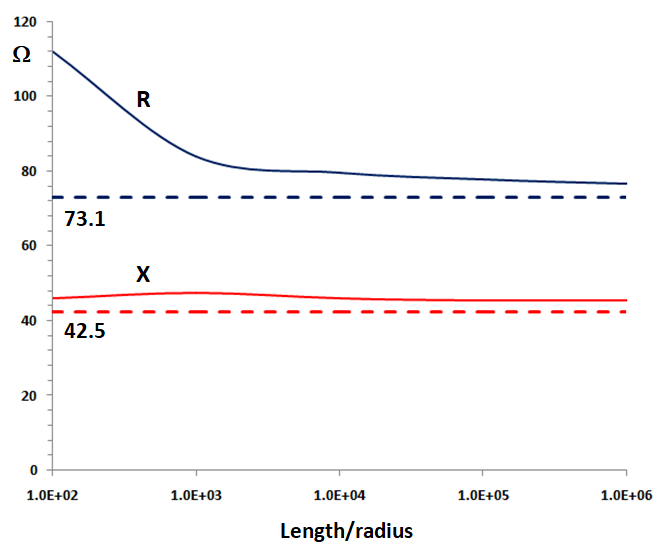
This result is really remarkable, since it is not common for it to be validated in other commercial implementations of the MoM.