• Search for:
    How Can We Help?

    Search for answers or browse our Knowledge Base.

    Guides | Models | Validation | Blog

    < All Topics
    Print

    Conformal Method of Moments

    Posted
    Updated

    The Method of Moments (MoM) is a technique used to convert the EFIE into a system of linear equations that then can be solved by standard methods. For simplicity, the integral (linear) operator in the Electric Field Integral Equation > (EFIE) will be denoted by L. Then, the EFIE takes the form:

    Eq. (1)

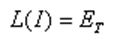
    where ET is the tangential component of the incident electric field. The current distribution is approximated by a sum of N basis functions with unknown amplitudes In, giving:

    Eq. (2)

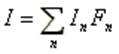
    With this expansion and using the linearity of the operator L, we can write:

    Eq. (3)

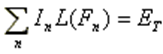
    To obtain a set of N equations, the functional equation (3) is weighted with a set of N independent testing functions wm, giving:

    Eq. (4)

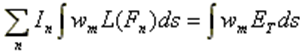
    where the integrals are calculated over the domain of L. Now we have as many independent equations as unknowns, so (4) can be written as:

    Eq. (5)

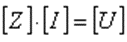
    where

    [Z]: impedance matrix with dimension NxN and the elements

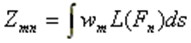
    [I]: current matrix with dimension Nx1 and the elements In.

    [U]: voltage matrix with dimension Nx1 and the elements

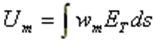
    This fully occupied equation system must be solved for the unknown currents In. LU decomposition is used in AN-SOF. The MoM is applied by first dividing the wire structure into N segments, and then defining the basis and testing functions on the segments. Triangular basis and pulse testing functions are used in AN-SOF, Fig. 1.

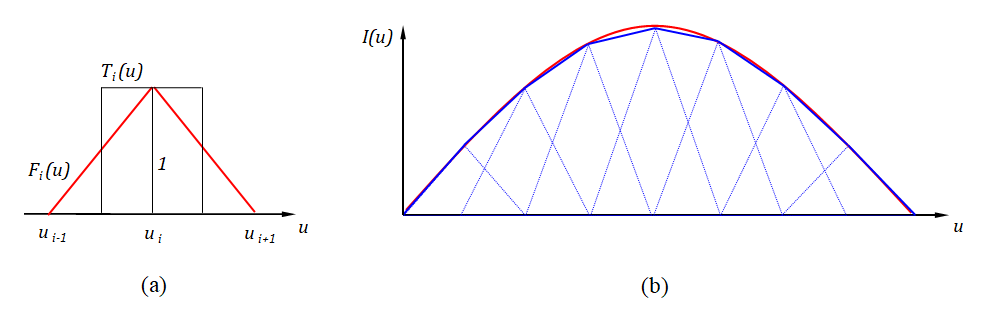
    Fig. 18.2: (a) Triangular basis functions, Fi(u), and pulse testing functions, Ti(u). (b) Current distribution approximated by triangular functions.

    When a curved wire is described parametrically by a vector function as in Eq. (5) here >, the basis and testing functions are curved in the sense that their support is a curved subset of the wire. Therefore, when curved basis and testing functions are used, the Conformal Method of Moments (CMoM) is obtained.

    To fill the impedance matrix [Z], an adaptive Gauss-Legendre quadrature rule is applied to compute the involved integrals. After having solved the equation system, the currents In are known and other parameters of interest, such as input impedances, voltages, radiated power, directivity, and gain can be computed.

    The MoM can also be used to calculate the electromagnetic response of metallic surfaces, which are modeled using wire grids. In AN-SOF, with the CMoM the accuracy of the calculation of wire grids is remarkably improved compared to the traditional MoM, as demonstrated in this article > . Another extension of the calculation includes wires that do not have a circular cross section. In AN-SOF an equivalent radius is calculated for these wires.

    Table of Contents