Search for answers or browse our Knowledge Base.
Guides | Models | Validation | Book
Experimenting with Half-Wave Square Loops: Simulation and Practical Insights
Explore the unique behavior of half-wave square loop antennas through AN-SOF simulations. Learn how conductor length affects current distribution and radiation patterns, with practical experiments to validate theory. Download our template to test configurations yourself!

Loop Antennas: Small vs. Large and Their Fundamental Differences
A loop antenna is a closed-circuit antenna formed by bending a conductor into one or more turns, bringing its two ends close together. Loops fall into two broad categories based on their dimensions relative to the operating wavelength:
- Small Loops – Where both the total conductor length and the largest linear dimension of a turn are much smaller than the wavelength (typically < 0.1λ).
- Large Loops – Where the conductor length and loop dimensions become comparable to or larger than the wavelength.
Small Loops: Coil-Like Behavior
A small loop behaves similarly to a large inductor, with nearly uniform current distribution—both in amplitude and phase—across the entire conductor. This condition holds as long as the total conductor length remains below approximately 0.1λ. Small loops are particularly useful for direction-finding applications and perform well as receiving antennas.
Large Loops: Non-Uniform Current Distribution
In contrast, large loops exhibit significant variations in both current amplitude and phase along their conductors. This non-uniform distribution produces radiation properties fundamentally different from small loops, making them ideal for array configurations requiring directional patterns.
Half-Wave Loop Antennas: Radiation Patterns and Performance Optimization
The Half-Wave Loop as a Radiator
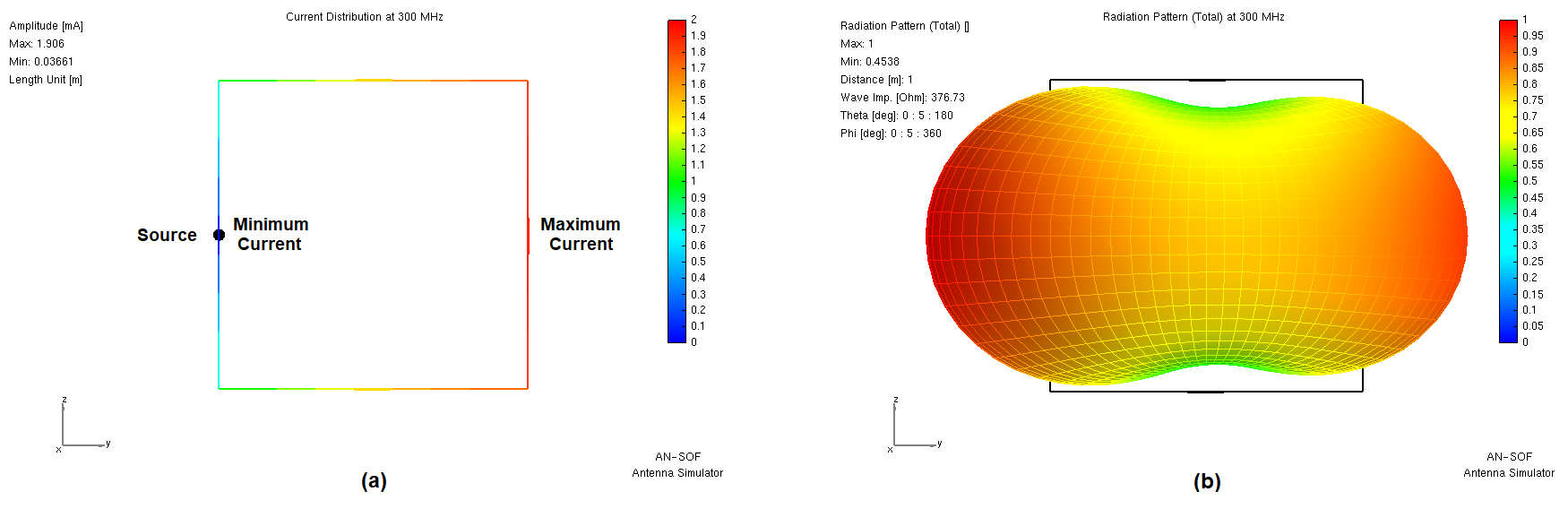
The smallest practical ‘large’ loop antenna typically features a conductor length of λ/2, frequently implemented as a square configuration with λ/8 sides. When center-fed on one side (Fig. 1a), it exhibits a closed-loop current distribution resembling a half-wave dipole—peaking at the center of the opposite side and minimizing at the feed terminals (source position). This current configuration generates maximum field strength in the loop’s plane, producing two primary radiation lobes in opposing directions (Fig. 1b).
Open-Loop Configuration
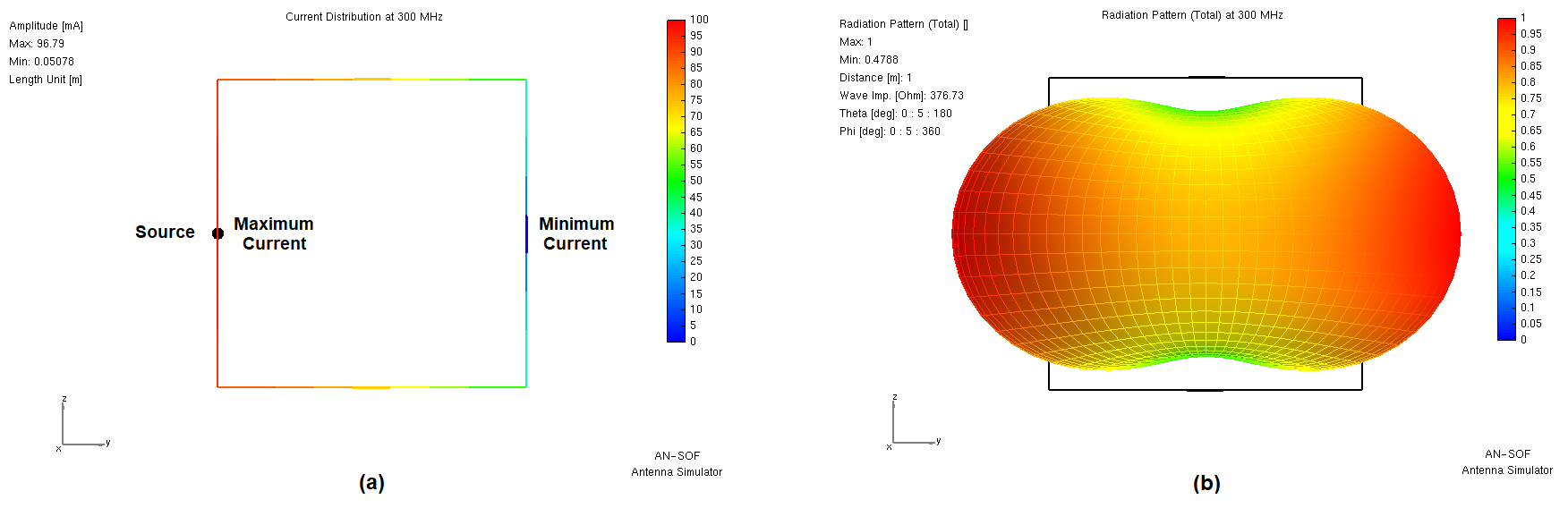
When the loop is opened at the center of the side opposite the feed (Fig. 2a), the structure no longer forms a closed loop, causing the current maximum to shift to the feed terminals. The resulting radiation pattern exhibits two main lobes in the plane of the loop (Fig. 2b), similar to Fig. 1 but now symmetrical.
Input Impedance Characteristics
- Closed-loop impedance (Fig. 1): Very high (several thousand ohms), as the feed-point current is at its minimum.
- Open-loop impedance (Fig. 2): Low (∼10 Ω), since the feed-point current reaches its maximum.
Enhancing Directivity and Gain
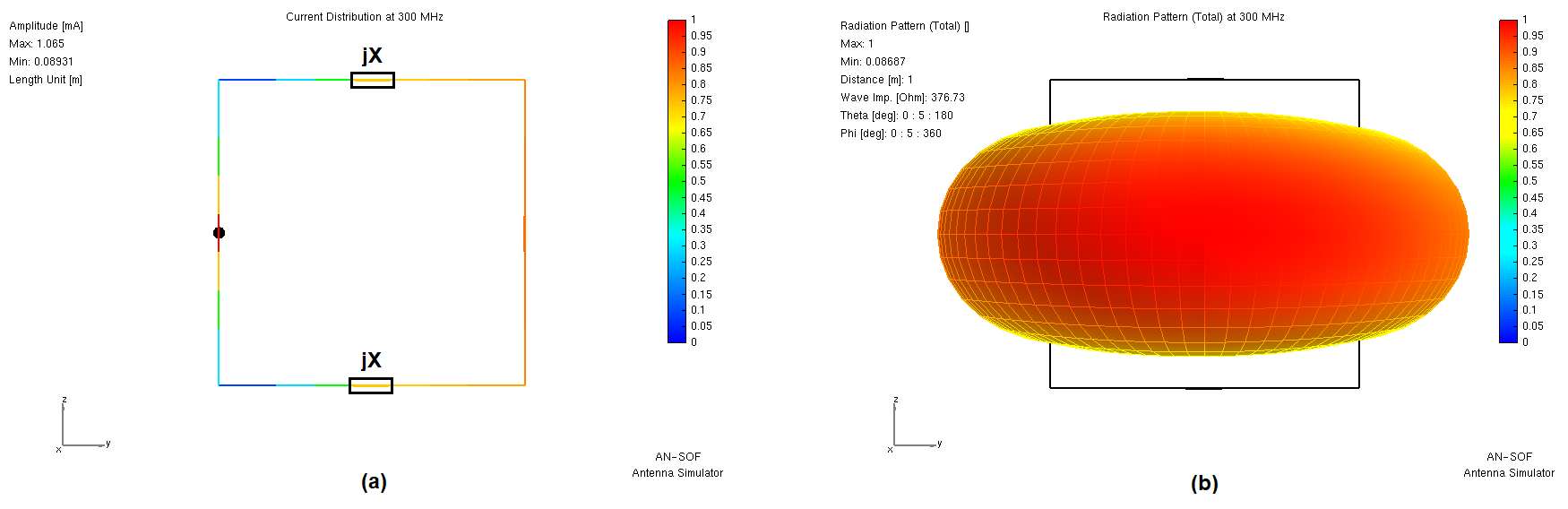
The closed loop’s directivity can be changed by loading the non-radiating sides (those connecting the driven and high-current sides) with inductive reactances (~ j 500 Ω) (Fig. 3). This technique:
- Reduces current in the loaded sides.
- Increases current in the driven side.
- Improves directivity, which can yielding ~1 dB gain over a half-wave dipole.
Caution: Lossy coils can significantly degrade this advantage, so high-Q components are essential.
Simulating a Half-Wave Square Loop in AN-SOF
This section introduces a practical AN-SOF simulation model of a half-wave square loop antenna (total conductor length = λ/2) that allows us to explore the behavior described theoretically. The model serves as a template to examine two key characteristics: the current distribution along the conductor and the distinctive radiation pattern that emerges when the loop dimensions approach half-wavelength proportions.
When analyzing the closed-loop configuration, we can observe how the current distribution follows a semi-sinusoidal pattern, peaking at the center of the side opposite the feed point. The resulting radiation pattern differs from the classic half-wave dipole’s donut shape due to the loop’s comparable size to the operating wavelength. Interestingly, by reducing the frequency until the loop becomes electrically small (approximately λ/10), the simulation demonstrates how the pattern transforms into the expected donut shape characteristic of small loops.
The model includes several adjustable parameters for experimentation. A lumped load element placed opposite the feed point allows us to switch between closed-loop (0 Ω) and open-loop (1E6 Ω) configurations with a simple parameter change. Additionally, the template incorporates the reactance loading scheme shown in Fig. 3, initially set to zero ohms but available for modification. We can insert reactances (jX) to study their effects on current distribution and radiation pattern.

Figure 4 shows an animated visualization of how the loop’s radiation pattern evolves with increasing frequency. The model’s physical dimensions were scaled to achieve a half-wave loop at 300 MHz (where λ ≈ 1m). Click the button below Figure 4 to download the model and begin experimenting. This hands-on demonstration bridges theoretical concepts with observable antenna behavior, providing essential insights for advanced design work.

