Beyond Analytical Formulas: Accurate Coil Inductance Calculation with AN-SOF

Traditional coil inductance calculations often rely on simplified approximations. AN-SOF offers a more accurate approach by considering factors like non-uniform magnetic fields, conductor losses, and complex coil geometries. By using AN-SOF, you can obtain precise inductance values, visualize magnetic field and current distributions, to improve your coil designs.

Introduction

Calculating the inductance of coils or solenoids has traditionally been challenging due to the complexity of their magnetic fields. The most common approach has been to simplify the problem by assuming a uniform magnetic field within the coil, neglecting edge effects, and representing the current flow as a uniform current sheet. However, these approximations can lead to inaccuracies, especially at higher frequencies and for coils with a diameter greater than their length.

In this article, we demonstrate how AN-SOF Antenna Simulator can provide a more accurate calculation of coil inductance by considering the non-uniform magnetic field distribution and other factors that are often overlooked in analytical methods.

The Idealized Current-Sheet Inductor

Traditional coil inductance calculations often rely on the idealized current-sheet inductor model. This model represents a solenoid with an infinitely thin conducting tape wound in a single layer, with zero spacing between turns but no electrical connection. While mathematically convenient, the current-sheet inductor simplifies the complex magnetic field distribution within a real coil.

For a very long current-sheet inductor, the magnetic field is approximately uniform along its length. In this case, the inductance of a cylindrical coil can be calculated using the following formula:

$\displaystyle L = \frac{\mu_0 \ \pi \ r^2 \ N^2}{l} \qquad (1) $

Where:

• $L$ is the coil inductance in Henries $[H]$
• $\mu_0$ is the permeability of free space ($4\pi \times 10^{-7} \ H/m$)
• $r$ is the coil radius in meters
• $N$ is the number of turns
• $l$ is the coil length in meters

It’s important to note that this formula is based on quasi-static assumptions, meaning it is valid for low frequencies since, as we can see, the value of $L$ obtained is independent of the frequency. Additionally, the conductor thickness is neglected, and the coil radius should be significantly smaller than its length ($r \ll l$).

Note: When referring to “coil length” ($l$), we mean the axial length of the coil, not the length of the wire used to wind the turns.

When the coil core is made of a ferromagnetic material, the formula for calculating inductance must be multiplied by the relative permeability of that material. The coil calculator below implements this formula, allowing us to estimate the inductance of an idealized current-sheet coil based on its diameter, length, and number of turns.

Idealized Current-Sheet Coil Inductance Calculator

Coil Diameter:

Coil Length:

Unit for Diameter and Length: mm inches

Number of Turns:

Core Relative Permeability:

Unit for Displaying Inductance: pH nH µH mH H

Calculate

Nagaoka’s Coefficient to Account for Non-Uniform Fields

The inductance formula for a long current-sheet coil (equation 1) becomes inaccurate when the coil length becomes comparable to its diameter, due to a non-uniform magnetic field distribution, especially at the coil ends. To address this, Hantaro Nagaoka, a renowned Japanese physicist, introduced a correction coefficient in 1909. This dimensionless factor, denoted by $k_L$, accounts for the coil diameter-to-length ratio and is incorporated into the inductance formula as shown:

$\displaystyle L = k_L \ \frac{\mu_0 \ \pi \ r^2 \ N^2}{l} \qquad (2) $

A calculator implementing this formula with Nagaoka’s coefficient can be found at: Single-Layer Circular Coil Inductance. However, it’s important to note that this calculator is based on Richard Lundin’s article “A Handbook Formula for the Inductance of a Single-Layer Circular Coil” (Proc. IEEE, Vol. 73, No. 9, pp. 1428-1429, Sept. 1985). This article details a handbook formula that incorporates Nagaoka’s table of coefficient values (160 entries).

Nagaoka’s meticulous calculations have been verified by numerous researchers. The significance of his work is evident by its inclusion in engineer’s slide rules, such as the Service Slide Rule Co. Reed Electronic model.

Wheeler’s Long-Coil Inductance Formula

Harold A. Wheeler’s “Simple Inductance Formulas for Radio Coils” (Proc. IRE, 1928, Vol 16, No. 10, pp. 1398-1400) introduced a simplified formula for calculating the inductance of long coils:

$\displaystyle L = \frac{r^2 \ N^2}{(9r + 10l)} \qquad (3)$

In this formula, the coil radius ($r$) and length ($l$) must be entered in inches, while the inductance is obtained in $\mu H$. Wheeler’s formula is reported to have an accuracy of ±1% when $l > 0.8r$. Therefore, it’s important to emphasize that this formula can be applied to relatively long coils and may not be accurate for very short coils. The accuracy deteriorates rapidly when the coil length is less than 0.4 times its diameter ($2r$).

Due to its simplicity, Wheeler’s formula has been widely implemented in various RF calculators available online. However, it’s essential to be aware of the limitations of this formula and ensure that the calculator you use checks for invalid entries.

Like the previous formulas discussed, Wheeler’s formula is based on the current-sheet approximation and is valid for quasi-static conditions. The calculator below implements equation (3) for estimating the inductance of long coils.

Wheeler’s Inductance Calculator

Coil Diameter:

Coil Length:

Unit for Diameter and Length: mm inches

Number of Turns:

Core Relative Permeability:

Unit for Displaying Inductance: pH nH µH mH H

Calculate

AN-SOF as a Coil Inductance Calculator

While AN-SOF was designed for antenna simulation, its capabilities extend to providing a more sophisticated coil model than the traditional current-sheet approach. Key features that enable this enhanced accuracy include:

• Curved Wire Segments: AN-SOF’s Conformal Method of Moments (CMoM) allows for curved wire segments that precisely follow the curvature of cylindrical coils. This eliminates the need for numerous straight segments used in traditional MoM methods, even for a single turn.
• Small Wire Spacing: AN-SOF can effectively handle small wire spacing between turns, which is often a limitation in traditional MoM implementations. This is particularly important for coils with tightly wound turns.
• Short Segments: AN-SOF can accurately model coils with very small dimensions compared to the wavelength. This is essential for many practical applications, such as coils used in high-frequency circuits.
• Thick Wires: The use of an Exact Kernel in AN-SOF allows for precise modeling of wire segments with a radius greater than their length, enabling the simulation of thick conductors often used in coil construction.

Due to these advantages, AN-SOF is a more practical tool for optimizing coil designs compared to traditional MoM-based software for wire structures. Additionally, AN-SOF can calculate a dispersive inductance, which accounts for the variation of inductance with frequency. This is especially important at higher frequencies where the quasi-static assumption breaks down.

Coils can be modeled in AN-SOF using the Helix wire primitive. To illustrate this, let’s consider a practical example: designing a 33 µH inductor for a short vertical antenna operating on the 160 m band. We want to wind a 12″ long, 2″ diameter air-core inductor using #10 AWG wire.

While the current-sheet inductance formulas (1), (2), or (3) can provide an initial estimate, AN-SOF can offer a more accurate calculation. By modeling the coil in AN-SOF, we can model the coil geometry precisely to achieve the desired inductance and even incorporate conductor losses to calculate the inductor’s quality factor ($Q$).

To expedite the explanation, a video tutorial and a downloadable coil template are provided below. The template features a helix with a 1A current source connected via linear wires, representing a real coil. The initial model consists of a 12″ long, 2″ diameter coil with 66 turns of #10 AWG copper wire. For a 160 m band application, the frequency is set to 1.9 MHz.

After running the calculations, the Results tab in AN-SOF will display the input impedance. To calculate the impedance only (excluding the radiated field, which is negligible in this case), use the shortcut “Ctrl + R.”

The video demonstrates the following steps:

1. Extracting Inductance: The input reactance, $X_{in}$, (imaginary part of the input impedance) is extracted and used to calculate the inductance using the formula $L = X_{in} / (2\pi f)$, where $f$ is the frequency in Hertz. Alternatively, you can use the Reactance to Inductance/Capacitance converter on our website.

2. Calculating Q: The inductor’s Q is calculated using the Inductor Quality Factor (Q) calculator on our website ($Q = X_{in}/R_{in}$), which requires the inductor’s internal resistance, $R_{in}$ (real part of the input impedance).

3. Modifying Coil Parameters: The video shows how to adjust the number of turns, segments (one segment per turn is sufficient at low frequencies), and wire radius. It also demonstrates how to change the helix radius and use the Scale Wires command in the Edit menu to modify the coil length.

The following table shows the differences that can be expected between the analytical formulas presented and the AN-SOF results, for inductance only, since the formulas do not incorporate conductor thickness or material:

$l$ / $2r$ / $N$	Idealized	Nagaoka	Wheeler	AN-SOF
12″ / 2″ / 66	36.4	34.0	33.8	33.5
12″ / 4″ / 12	4.81	4.20	4.17	5.55
6″ / 4″ / 12	9.63	7.41	7.38	8.06

We encourage users to increase the frequency to observe the dispersive behavior in the coil inductance. When increasing frequency, take into account that more segments per turn will be needed.

Once the inductance (L) and internal resistance (R) of a coil have been determined using AN-SOF, it’s often more efficient to incorporate the coil into an antenna model as a lumped series impedance (RL). This RL element can be conveniently placed across a selected segment within the antenna model, where the values of R and L are directly entered. By adopting this approach, the coil calculation project can be separated from the antenna design process, simplifying the overall modeling complexity and improving efficiency.

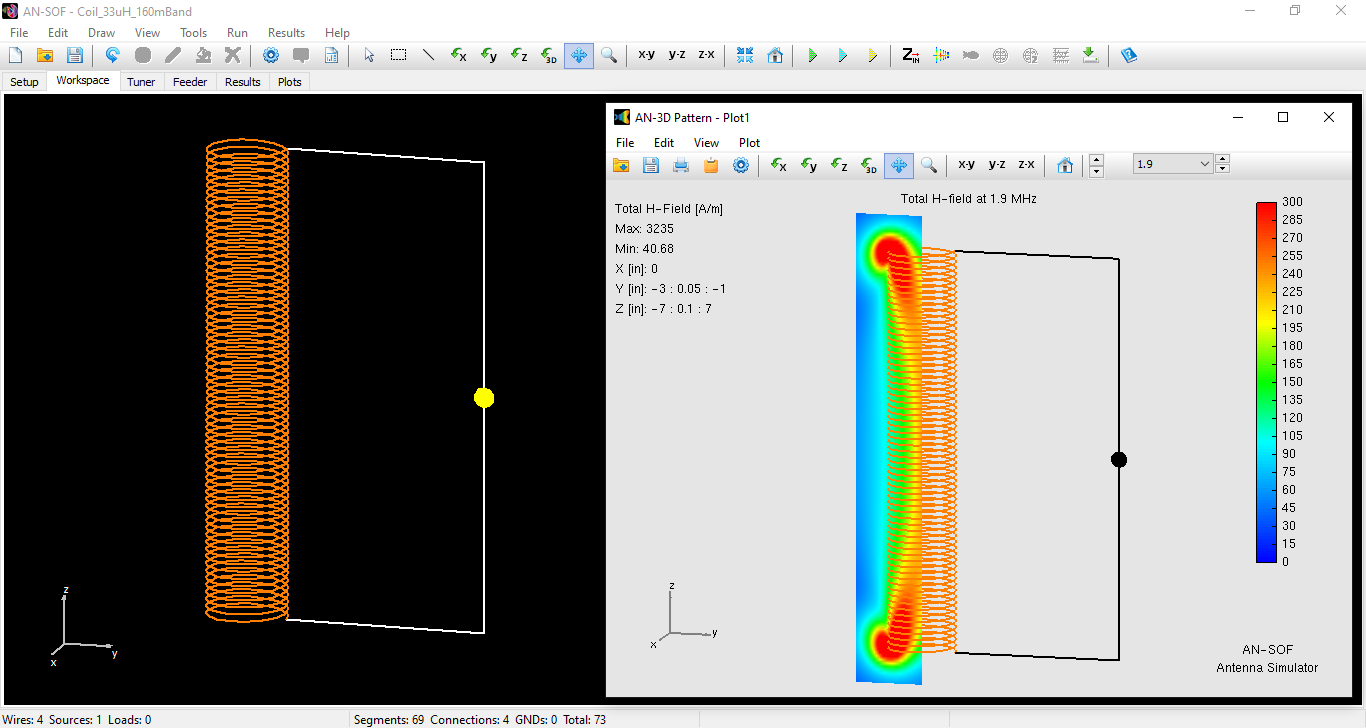
Figure 1 illustrates the coil model (left) and its near magnetic field distribution (right). As observed, the magnetic field is not uniform, even though this coil could be considered “long enough” for formula (1). The concentration of the magnetic field at the coil’s ends is particularly noticeable.

AN-SOF also calculates the current distribution, as shown in Figure 2(a). While the scale may not reveal subtle differences in current intensity along the coil, the color distribution indicates that the current is stronger at the coil’s center compared to its ends. This observation is further confirmed by plotting the current linearly along the coil’s length, as depicted in Figure 2(b).

It’s important to note that circuit theory assumes a constant current throughout the coil, equal to the source current (1A in this case). However, AN-SOF reveals that this is a quasi-static approximation (valid at low frequencies) and small deviations from the uniform current distribution can be observed. These microscopic differences are neglected in traditional circuit analysis.

Conclusion

In this article, we have explored the challenges of calculating coil inductance and presented various formulas. Traditional approaches, such as the idealized current-sheet inductor model, Nagaoka’s coefficient, and Wheeler’s formula, provide simplified approximations that can be useful in certain scenarios. However, for more precise calculations, particularly for short coils where the magnetic field distribution is more complex, AN-SOF Antenna Simulator offers a more accurate approach.

By leveraging AN-SOF’s advanced features, including curved wire segments, small wire spacing, short segments, and thick wire modeling, we can obtain more accurate inductance values, taking into account factors that are often neglected in analytical methods. Additionally, AN-SOF allows for the calculation of dispersive inductance, which is crucial at high frequencies.

The ability to visualize the coil magnetic field and current distribution provides valuable insights into its behavior and helps in optimizing its design. By combining analytical techniques with AN-SOF simulations, we can achieve a deeper understanding of coil inductance and develop more efficient and reliable designs.

---