
AN-SOF Antenna Simulation Software
Accurate, Fast, and Easy-to-Use Tool for Antenna Modeling, Analysis, and Design
Welcome to AN-SOF!
Congratulations on choosing AN-SOF, the best combination of ease of use and accuracy you can find in an electromagnetic simulator for the modeling and design of antennas and wire structures in general. This User Guide describes AN-SOF and its many features in detail. Here, you will also find step-by-step examples and tips to help you quickly progress with your antenna modeling projects.
Table of Contents
📖 Getting Started
⚙ Simulation Setup
✏ Drawing Wires
📡 Grids and Surfaces
🔌 Sources and Loads
📶 Incident Field
🛣 Ground Planes
🧮 Running Calculations
📈 Displaying Results
➡ Transmission Lines
📗 Step By Step
🎓 Background Theory
❓ Frequently Asked Questions
Getting Started
Enhancing Antenna Design Through Simulation Software
An antenna model represents a real-world antenna within a computer program. It is important not to confuse this type of model with a scale model, which is sometimes constructed to measure the radiation characteristics of a larger, physically identical antenna. Due to the mathematical complexity involved in modeling, specialized software is often used to predict and analyze antenna performance.
Computer simulation plays a critical role in overcoming challenges and driving innovation throughout the product development lifecycle. A computer model offers significant advantages, including the ability to modify, redesign, break, destroy, and rebuild designs multiple times without wasting physical materials. By leveraging simulation software, engineers can significantly reduce the costs associated with building successive physical prototypes, streamlining the design process.
AN-SOF is a comprehensive simulation software suite designed for antenna modeling and optimization. It supports the design of a wide range of wire antennas, including dipoles, monopoles, Yagis, log-periodic arrays, helices, spirals, loops, horns, fractals, phased arrays, and many other types. Additionally, AN-SOF enables detailed modeling of feeding systems using transmission lines, allowing users to analyze complex antenna configurations with precision. The software can simulate antennas positioned above lossy ground planes or broadcast antennas above radial wire ground screens, providing realistic and accurate results.
Furthermore, AN-SOF’s calculation capabilities have been extended to include single-layer microstrip patch antennas and the computation of radiated emissions from Printed Circuit Boards (PCBs). As a result, AN-SOF is a powerful tool for Electromagnetic Compatibility (EMC) applications. The software also supports passive circuits with lumped impedances and non-radiating networks, enabling comprehensive analysis of antenna systems.
Note
In the realm of antenna applications, AN-SOF proves invaluable as it empowers users to achieve the following:
- Design superior antennas.
- Predict and optimize antenna performance.
- Fine-tune antenna parameters for optimal results.
- Account for environmental effects on antenna performance.
- Employ script-based optimization to refine designs.
- Gain valuable insights into antenna behavior.
- Experiment multiple times prior to physically building the antenna model.
- Deepen understanding of antennas and their properties.
- Facilitate knowledge sharing and collaboration with colleagues.
With AN-SOF at your disposal, you can explore the exciting possibilities of antenna analysis and optimization. The software provides an extensive toolkit for designing, evaluating, and enhancing antenna performance, empowering engineers and enthusiasts alike to push the boundaries of innovation.
Note
AN-SOF enables us to perform a wide range of tasks, including:
- Describing the antenna’s geometry accurately.
- Selecting appropriate construction materials.
- Specifying the environmental and ground conditions.
- Determining the antenna’s height above the ground.
- Analyzing the radiation pattern and front-to-back ratio.
- Plotting directivity and gain.
- Evaluating impedance and SWR (Standing Wave Ratio).
- Predicting bandwidth.
- Obtaining numerous additional parameters and plots.
Drawing the geometry of structures in AN-SOF is intuitive and user-friendly. Wires can be created in a 3D space using the mouse, menus, and easy-to-navigate dialog windows. Tools are available to zoom, move, and rotate the structure, ensuring precise control over the design process.
To visualize simulation results, AN-SOF integrates seamlessly with a suite of specialized applications: AN-XY Chart, AN-Smith, AN-Polar, and AN-3D Pattern. These tools allow users to display graphs and analyze data effectively. They can also be executed independently for further graphic processing, offering flexibility and convenience for advanced users.
With AN-SOF and its software suite for displaying graphics, we have all the necessary tools to guide us through the stages of an antenna design process.
Introduction to AN-SOF: Antenna Simulation Essentials
AN-SOF performs computations of electric currents flowing on metallic structures, including antennas in transmitting and receiving modes, as well as scatterers. A scatterer refers to any object capable of reflecting and/or diffracting radiofrequency waves. For instance, wave scattering analysis can be conducted on the surface of an aircraft to determine optimal antenna placement, on a parabolic reflector to examine gain in relation to the reflector shape, or on a car’s chassis to predict interference effects.
The Method of Moments (MoM) stands as one of the most widely validated techniques for antenna simulation. AN-SOF incorporates an enhanced and advanced version of this method called the Conformal Method of Moments (CMoM) with Exact Kernel, which addresses various challenges associated with traditional MoM approaches and achieves unparalleled accuracy.
Interested in learning more about the CMoM implementation in AN-SOF? Read this article:
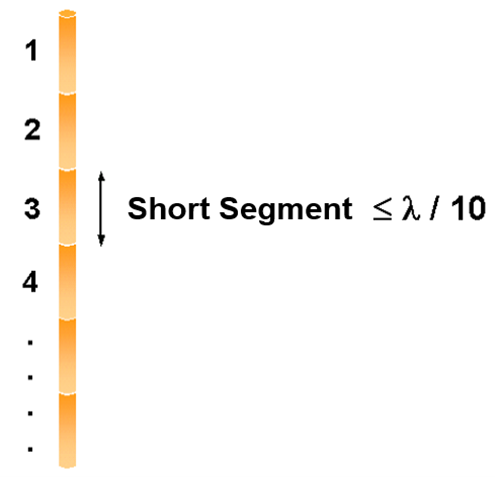
According to the MoM, any metallic structure can be represented using conductive wires, as illustrated in Fig. 1. These wires are subdivided into small segments, which assume the shape of cylindrical tubes. To obtain accurate results, the length of each wire segment should be comparatively short compared to the wavelength, as depicted in Fig. 2. However, this concern can be alleviated during the initial simulation since AN-SOF automatically handles the segmentation of wires.
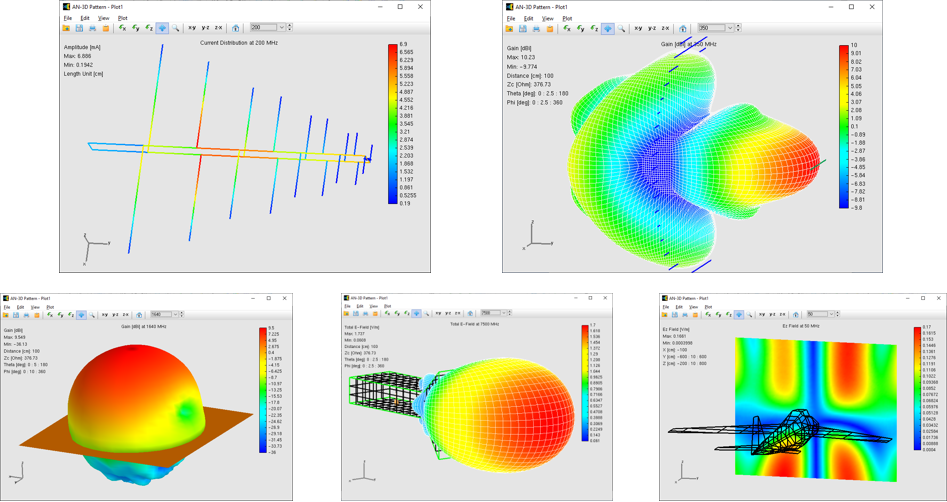
The flow of electric currents within the structure can be achieved by introducing a voltage generator at a specific location operating at a given frequency. Current generators can also serve as the excitation source, alongside plane waves impinging on the structure from distant sources. Once the geometry, materials, and sources of the structure are defined, the computation can be executed to determine the currents flowing through the wire segments. Generally, these electric currents exhibit varying intensities along and across the structure, collectively referred to as a current distribution. Fig. 3 showcases an example of the current distribution on a log-periodic antenna.
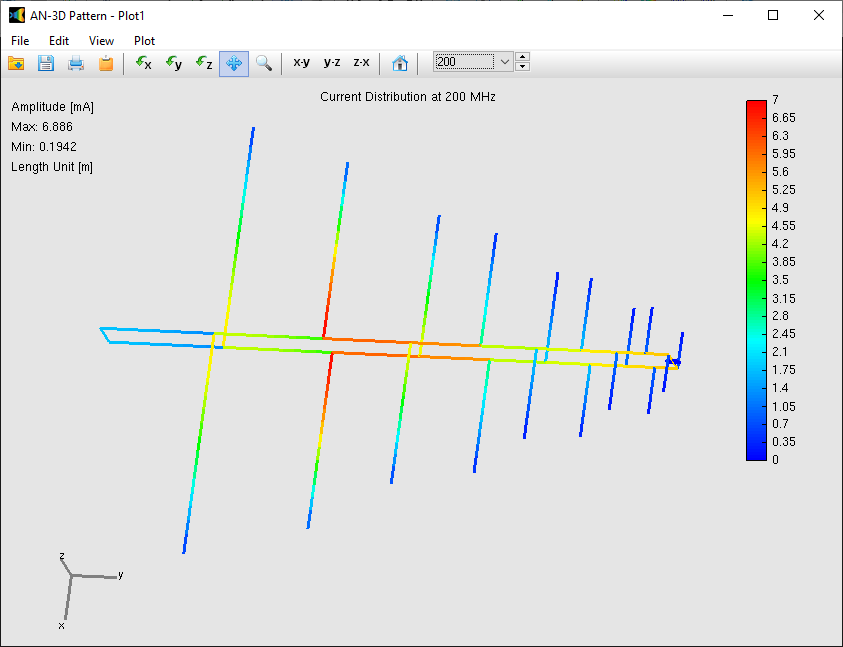
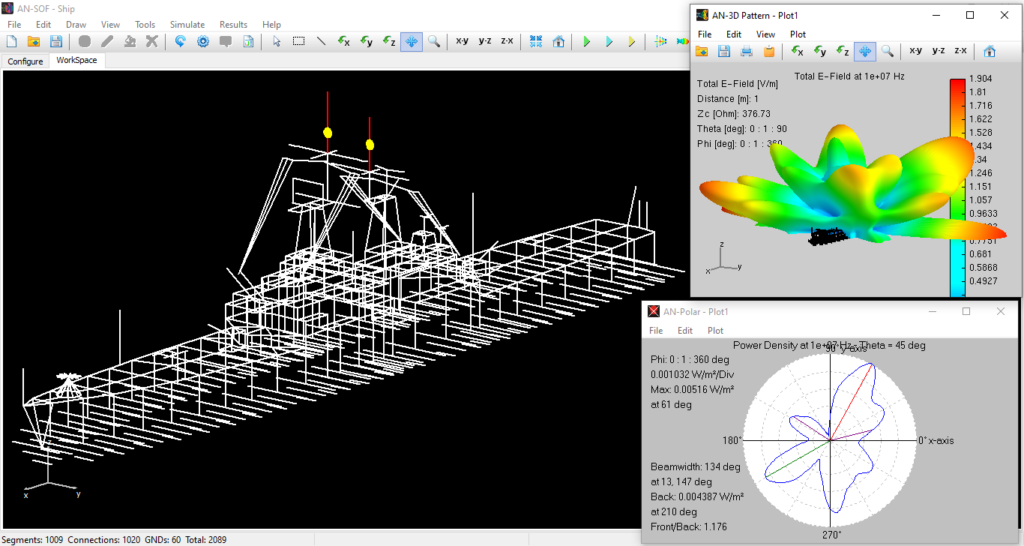
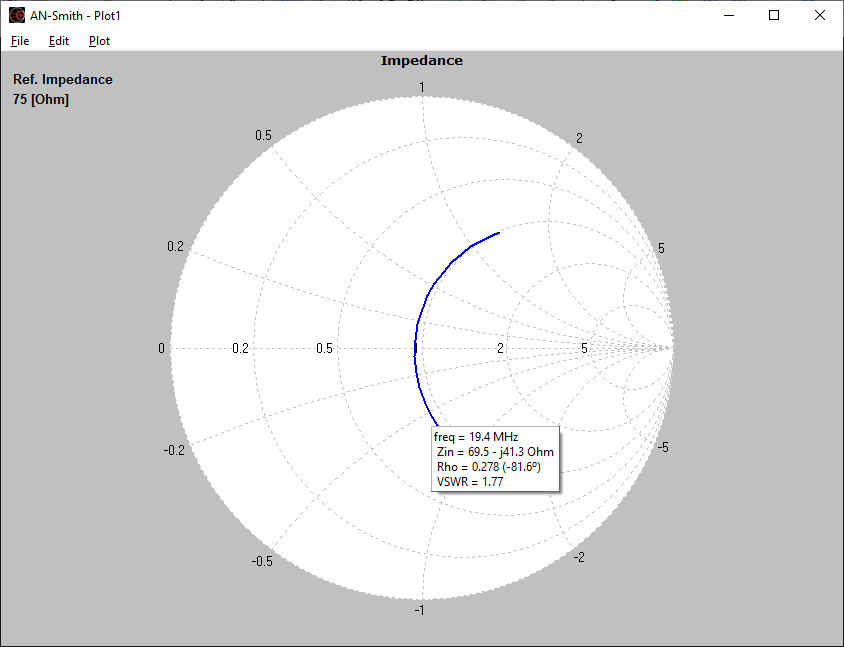
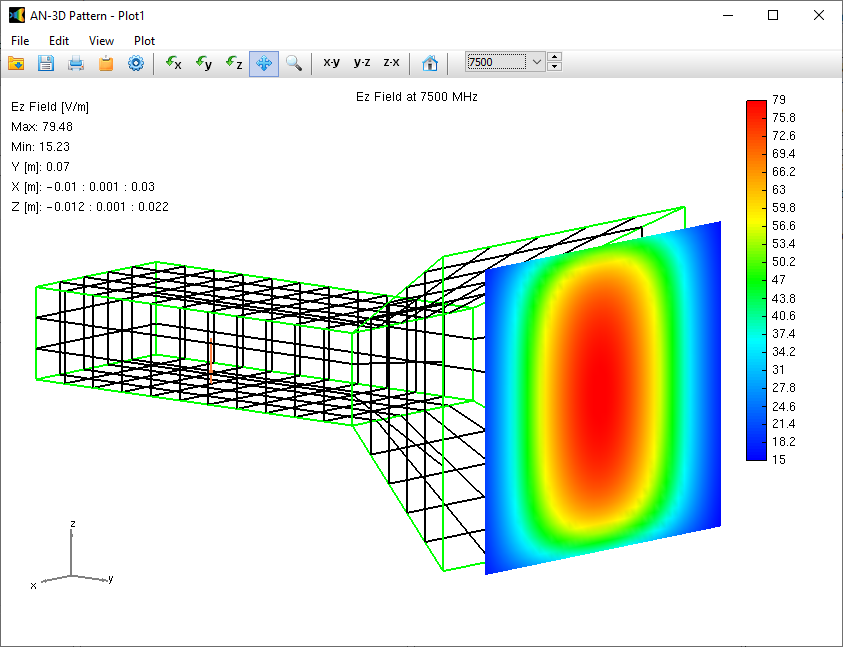
In the subsequent phase of the simulation process, the electromagnetic field radiated by the current distribution can be calculated. However, the current distribution itself provides valuable insights into the behavior of the structure, particularly when a frequency sweep is conducted. In the case of antennas, the feed point impedance can be analyzed as a function of frequency to assess the bandwidth. The Voltage Standing Wave Ratio (VSWR) can be plotted on a Smith chart for better interpretation of the results, as demonstrated in Fig. 4. The electric and magnetic fields in the proximity of the structure, known as the near-field zone, can be obtained and visualized as a color map, with intensities often resembling temperature maps used in weather forecasts, as shown in Fig. 5.
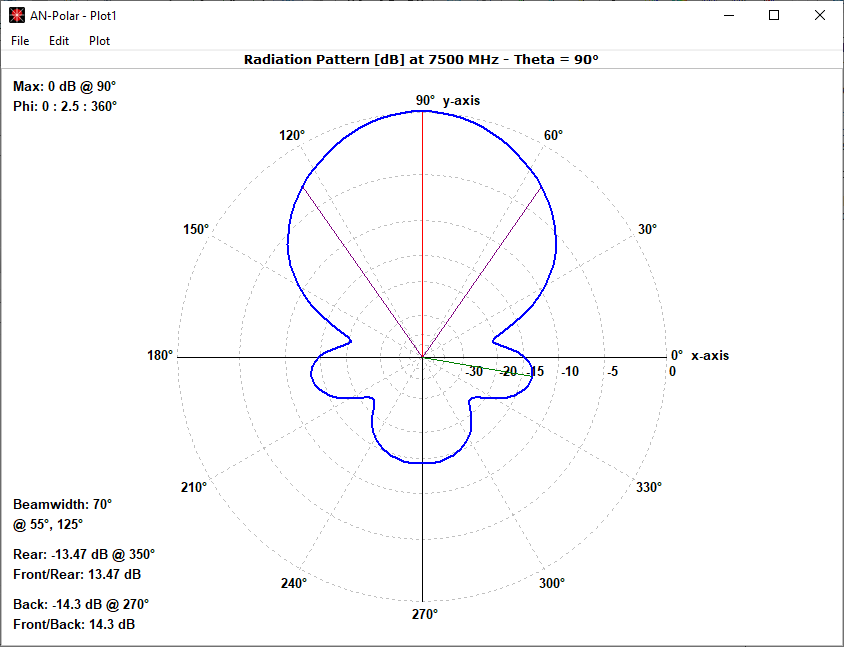
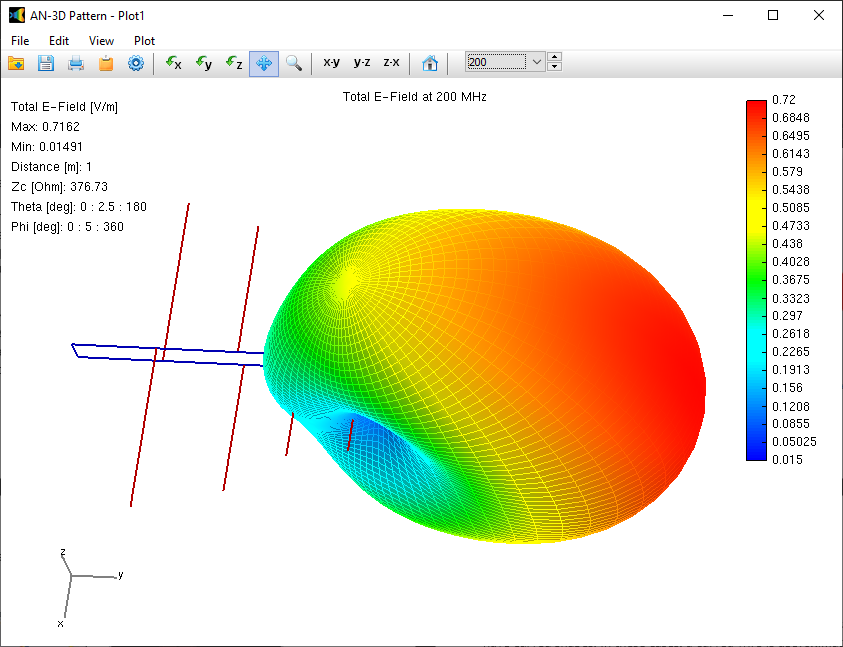
In the far-field zone, situated several wavelengths away from the structure, the magnetic field becomes proportional to the electric field. As a result, the electric field intensities are commonly used to analyze the results. This region is depicted in polar diagrams, as illustrated in Fig. 6, where the radiated field is represented as a function of direction. A more comprehensive representation can be achieved by plotting a 3D pattern, where radiation lobes can be superimposed onto the structure’s geometry, providing enhanced visualization of its directional properties, as exemplified in Fig. 7.
AN-SOF stands out as the easiest-to-use software tool for simulating antennas, particularly those that can be modeled using conductive wires. Are you ready to embark on your first simulation? Let’s get started!
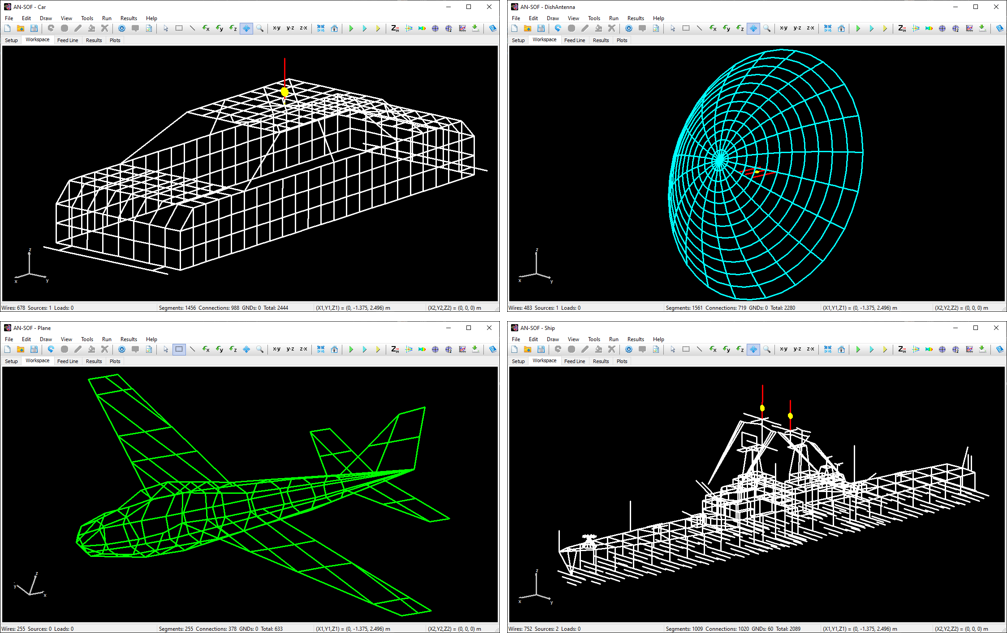
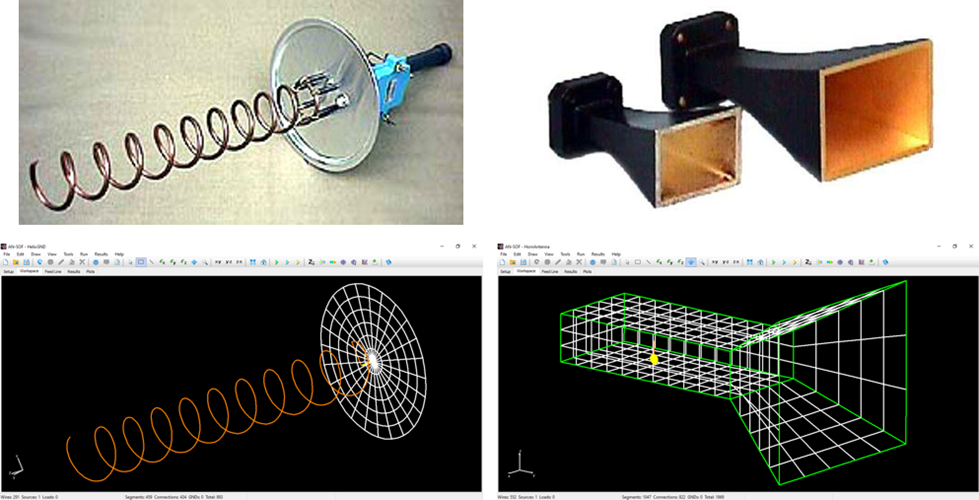
Explore Our Pre-Computed Examples in the Models Tab
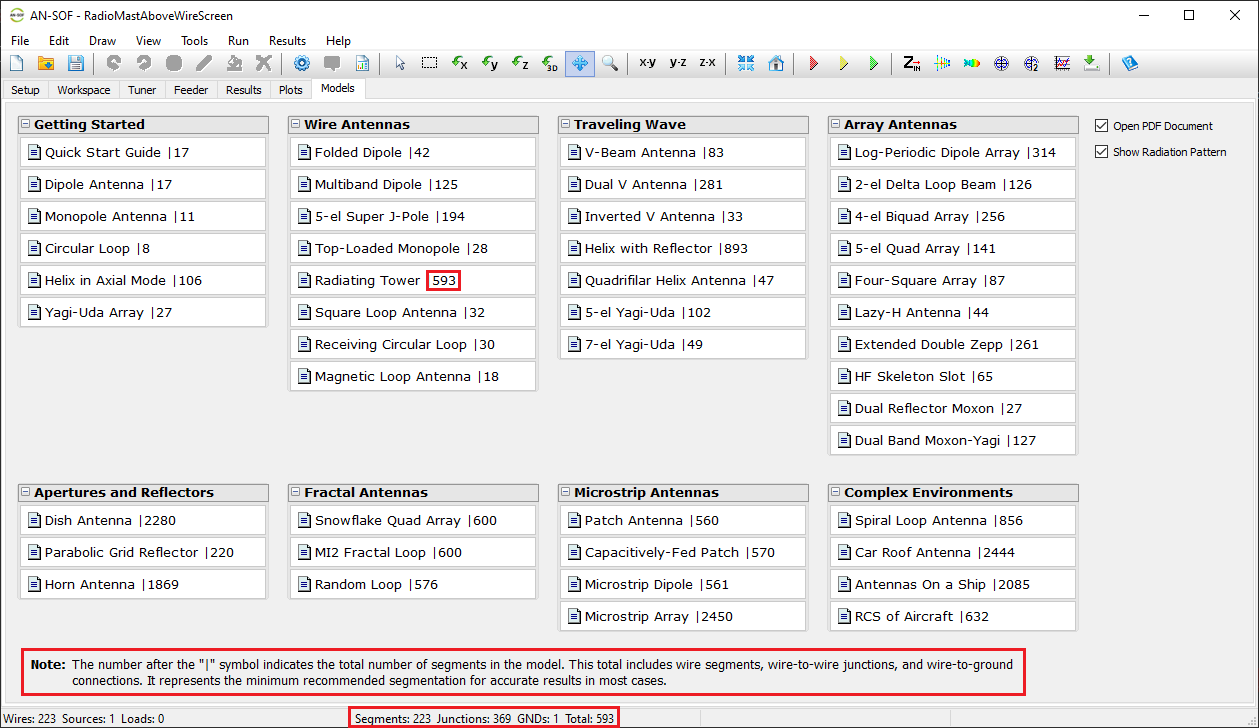
AN-SOF includes a collection of pre-calculated models that enable users to quickly load example projects directly into the interface. These models are organized into categories for easy navigation, making this feature especially useful for users exploring example designs and learning key antenna concepts.
In the Models tab, you’ll find quick-access buttons for opening example models (see Fig. 8). Each model displays a 3D radiation pattern and includes a PDF guide with informational resources. Since all models are pre-calculated, they can be opened and explored using the AN-SOF Trial version.
The total number of segments used in each model is displayed after the “|” symbol on each button label in the Models tab, as well as in the Status Bar at the bottom of the AN-SOF window. This total includes:
- Wire segments
- Wire-to-wire junctions
- Wire-to-ground connections (labeled as “GNDs”)
Note:
The AN-SOF Trial version supports models with up to 50 total segments. If you modify an example model and exceed this limit, you’ll need an active license for the AN-SOF PRO Edition to run additional simulations.
To explore the example models, simply click the buttons in the Models tab. On the right side of the screen, you can use the options “Open PDF Document” and “Show Radiation Pattern” to toggle the display of the PDF guide or the radiation pattern plot as needed.
Performing the First Simulation with AN-SOF
Several example files are included in the AN-SOF installation directory, located within a folder named “Examples”. When opening a file with the extension “.emm”, the wire structure will be displayed on the screen. To run the calculation, click on the Run ALL button on the toolbar. The main results can be plotted by clicking on the following buttons: Plot Current Distribution, Far-Field 3D Plot, and Far-Field Polar 1 Slice.
As a first experience using AN-SOF, let’s simulate a standard half-wave dipole, which is one of the simplest antennas that can be modeled. A dipole is a straight wire that is fed at its center. When the wire’s cross-section is circular, it is referred to as a cylindrical antenna. Since the wire is typically made of a highly conductive material, it can be considered a perfect conductor with zero resistivity. Therefore, we will model a cylindrical antenna with zero resistivity in this example. Follow the steps below to perform this simulation.
Step 1: Setup
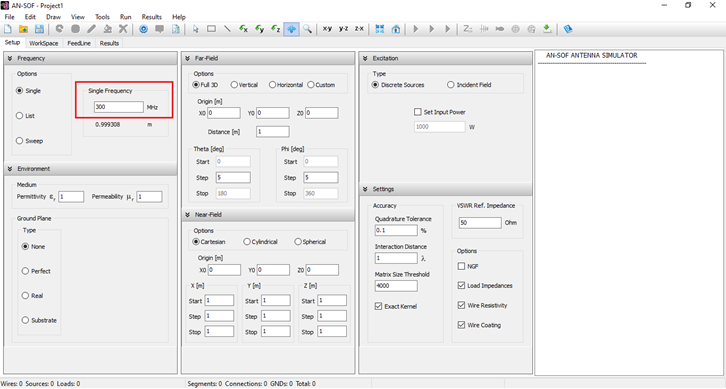
The first step is to set the operating frequency. Navigate to the Setup tab in the AN-SOF main window. Within the Frequency panel, there are three options to choose from. Select Single and enter the operating frequency for the antenna (see Fig. 9). In this case, the frequency is given in megahertz (MHz), and lengths are measured in meters (m). If desired, you can change the unit system for frequencies and lengths by going to Tools > Preferences. Please note that for a frequency of 300 MHz, the wavelength is approximately 1 meter (0.999308 m).
Step 2: Draw
Once the operating frequency has been set, you can draw the antenna geometry on the Workspace tab. The workspace is where the wire structure is visualized, representing a 3D space that allows zooming, rotation, and movement.
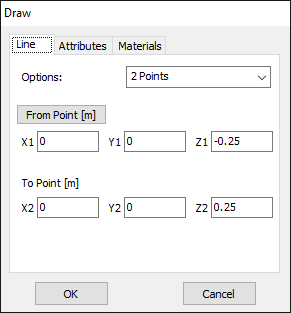
In AN-SOF, a straight wire is referred to as a Line. To draw a line, go to the main menu and select Draw > Line. This will open the Draw dialog box. In the Line tab, you can set the coordinates of two distinct points.
For this example, we will create a line along the z-axis that is 0.5 meters long, corresponding to half a wavelength at 300 MHz. Figure 10 illustrates the chosen starting point of the line at (X1, Y1, Z1) = (0, 0, -0.25) m, and the ending point at (X2, Y2, Z2) = (0, 0, 0.25) m. Next, switch to the Attributes tab (see Fig. 11). To ensure accurate results, the line should be divided into segments that are relatively short compared to the wavelength. Generally, a segment length equal to or less than one-tenth of a wavelength is considered short. AN-SOF suggests a minimum number of segments to achieve reliable results automatically. If you require higher resolution, you can increase the number of segments.
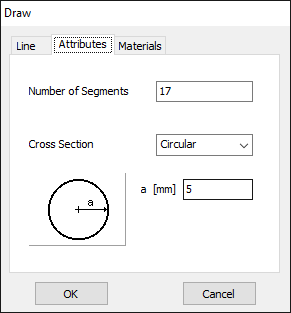
In this case, the line will be divided into 17 segments, and the wire cross-section will be circular with a radius of 5 millimeters. On the Materials tab (refer to Fig. 12), you can set the wire’s resistivity to zero.
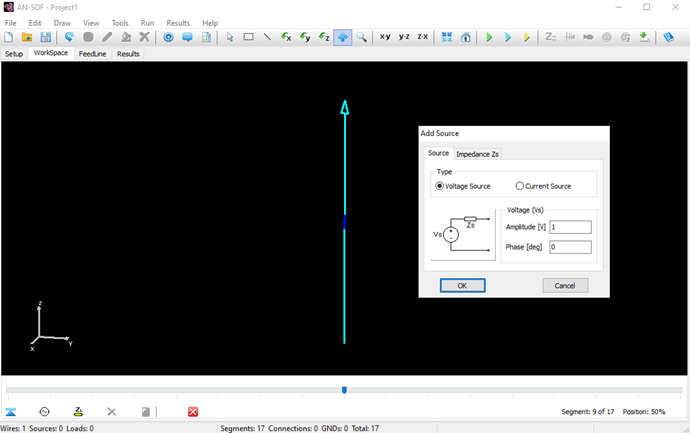
The next step is to feed the dipole. Right-click on the wire and select the Source/Load command from the pop-up menu that appears. A toolbar with a slider will be displayed at the bottom of the screen. Move the slider to the segment located at the center of the wire. Then, click the Add Source button. Add a voltage source with an amplitude of 1 Volt and a phase of zero (see Fig. 13).
Step 3: Run
To run the calculation, go to Run > Run Currents in the main menu. Once the calculations are completed, proceed to Run > Run Far-Field in the main menu. This will calculate the current distribution on the dipole antenna and the radiated field.
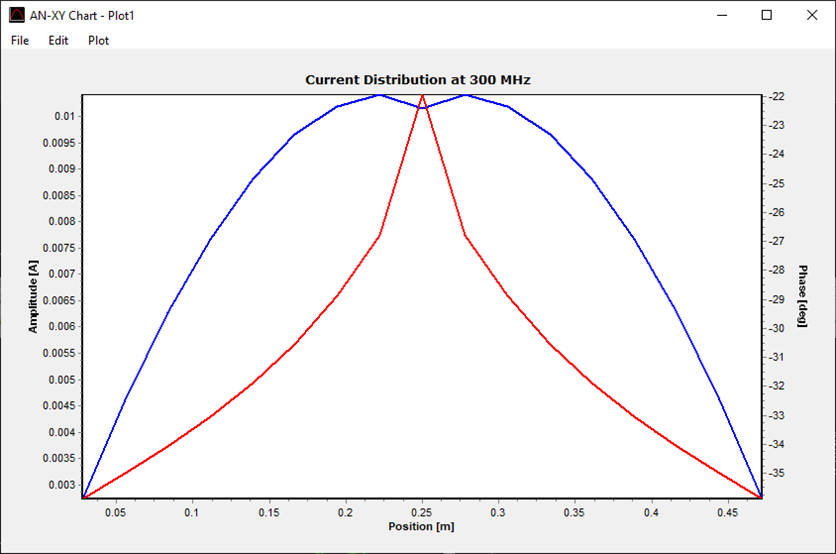
AN-SOF provides integrated graphical tools for result visualization. Right-click on the wire and select Plot Currents from the displayed pop-up menu. A plot showing the current distribution in amplitude along the dipole antenna will be displayed (refer to Fig. 14). Since a half-wave dipole has been drawn, the resulting current distribution resembles a semi-cycle approaching a sine function.
You can obtain several parameters from the perspective of the voltage source connected to the antenna terminals. Right-click on the wire and select List Currents from the pop-up menu. Move the slider to the position of the voltage source and click on the Input List button. This will display the input impedance of the dipole antenna, along with many other parameters (see Fig. 15).
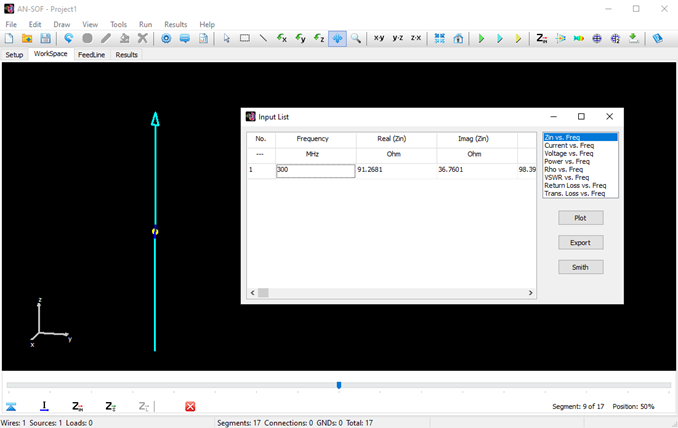
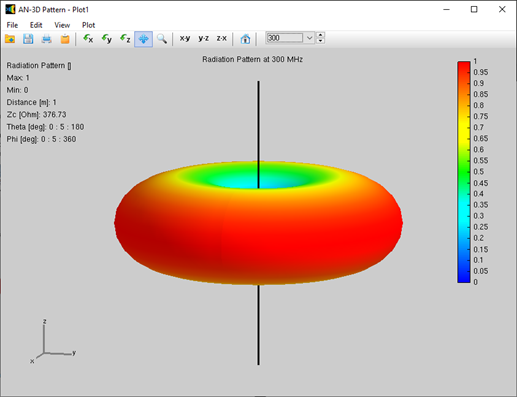
Alternatively, you can obtain the input impedance by simply clicking on the List Input Impedances (Zin) button in the main toolbar. To represent the radiation pattern in a 3D plot, navigate to Results > Plot Far-Field Pattern > 3D Plot in the main menu. The normalized radiation pattern will be displayed in the AN-3D Pattern application. A color bar-scale indicates the field intensities over the radiation lobes. Additionally, you can plot the directivity, gain, and electric field patterns by accessing the Plot menu in AN-3D Pattern. In the case of a half-wave dipole, it exhibits omnidirectional characteristics in the plane perpendicular to the dipole axis (xy-plane) (refer to Fig. 16).
As you have just experienced, a simulation consists of three simple steps. We hope you have enjoyed this example. For additional step-by-step examples, please visit our section titled Examples > Step by Step.
Summary
The key advantages of AN-SOF can be summarized as follows:
- AN-SOF is antenna modeling and design software that offers fast and user-friendly input and output graphical interfaces.
- AN-SOF employs the Conformal Method of Moments with Exact Kernel, resulting in enhanced accuracy and speed.
- AN-SOF provides an extended frequency range, enabling simulations from extremely low frequencies (such as 60 Hz circuits) to microwave antennas.
Simulating a wire structure involves a three-step procedure:
- Setup: Set frequencies, environment, and desired results.
- Draw: Draw the geometry, specify materials, and add sources.
- Run: Perform the calculation and visualize the results.
At the beginning of the simulation, you can choose a convenient unit system for frequencies and lengths. This choice can be adjusted later by accessing Tools > Preferences. For instance, wire lengths are typically measured in meters (m) or feet (ft) for frequencies below 100 MHz, while millimeters (mm) or inches (in) are commonly used for higher frequencies.
Features and Capabilities
AN-SOF is a comprehensive software tool for the modeling and simulation of antenna systems and radiating structures in general.
AN-SOF is intended for solving problems in the following areas:
- Modeling and design of wire antennas.
- Antennas above a lossy ground plane.
- Broadcast antennas over radial wire ground screens.
- Single layer microstrip patch antennas.
- Radiated emissions from printed circuit boards (PCBs).
- Electromagnetic Compatibility (EMC) applications.
- Passive circuits, transmission lines, and non-radiating networks.
AN-SOF is based on an improved version of the so-called Method of Moments (MoM) for wire structures. Metallic objects like antennas can be modeled by a set of conductive wires and wire grids, as it is illustrated in Fig. 1. In the MoM formulation, the wires composing the structure are divided into segments that must be short compared to the wavelength. If a source is placed at a given location on the structure, an electric current will be forced to flow on the segments. The induced current on each individual segment is the first quantity calculated by AN-SOF.
Once the current distribution has been obtained, the radiated electromagnetic field can be computed in the far- and near-field zones. Input parameters at the position of the source or generator can also be obtained, such as the input impedance, input power, standing wave ratio (SWR), reflection coefficient, transmission loss, etc.
The modeling of the structure can be performed by means of the AN-SOF specific 3D CAD interface. Electromagnetic fields, currents, voltages, input impedances, consumed and radiated powers, directivity, gain and many more parameters can be computed in a frequency sweep and plotted in 2D and 3D graphical representations.
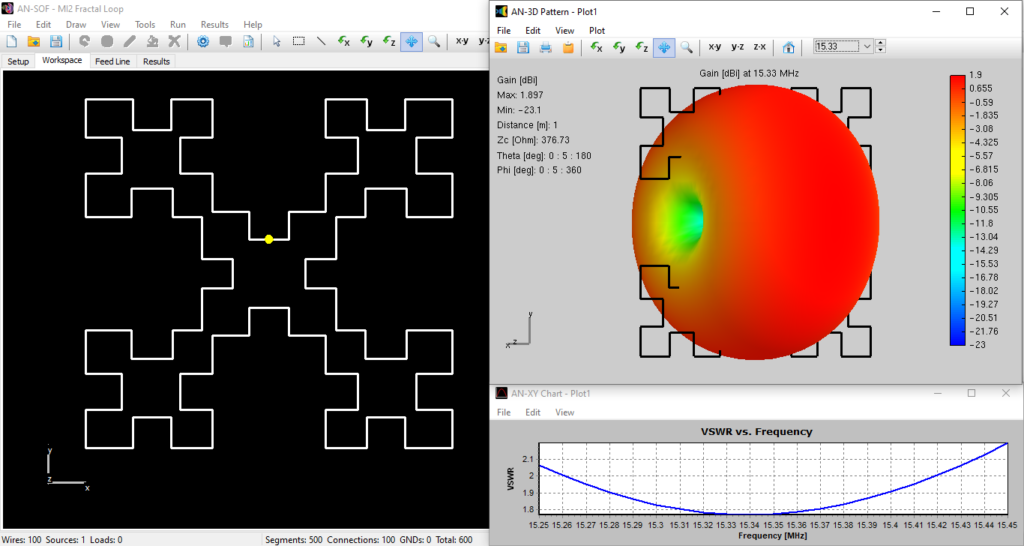
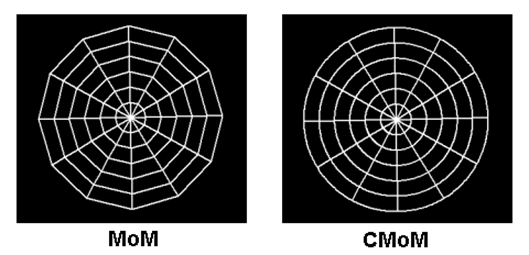
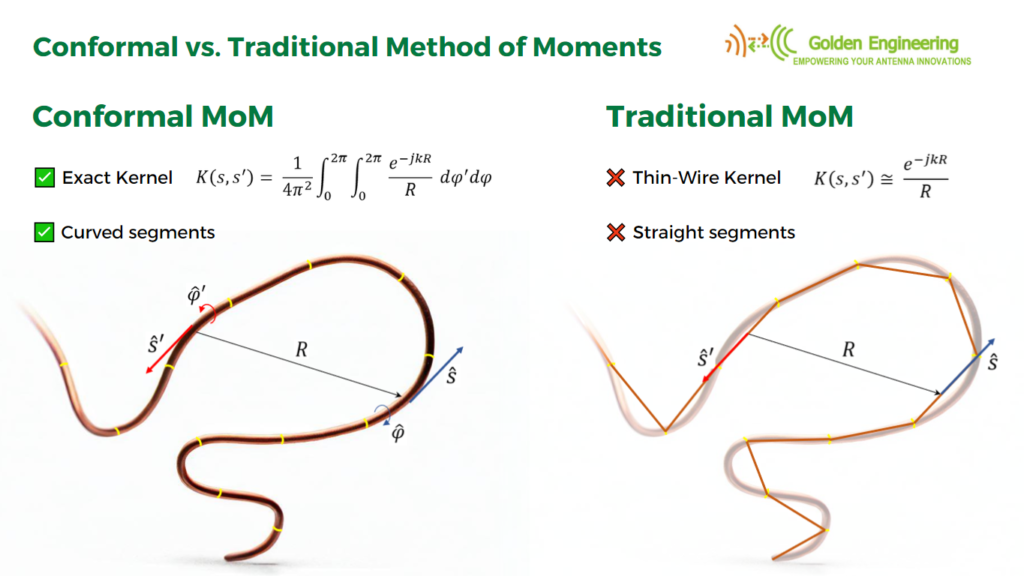
In the case of curved antennas like loops, helices, and spirals, the MoM in AN-SOF has been improved to accurately account for the wire’s exact curvature. Traditional calculations often use straight-line segments to approximate curved antennas, resulting in many discontinuous wire junctions. This linear approximation can be inefficient in terms of computer memory and the number of calculations required, as it necessitates multiple straight segments to mimic the smooth curvature of wires. To address this issue, AN-SOF uses curved segments that precisely follow the contours of curved antennas. This innovative technique is known as the Conformal Method of Moments (CMoM).
As an example, Fig. 2 shows the different approaches to a circular disc obtained by means of the MoM and CMoM methods. Both methods are available in AN-SOF since the MoM is a special case of the more general CMoM.
In addition to the CMoM capabilities, advanced mathematical techniques have been implemented in the calculation engine making possible simulations from extremely low frequencies (e.g., electric circuits at 50-60 Hz) to very high ones (e.g., microwave antennas above 1 GHz).
In what follows, a summary of the modeling options and the simulation results that can be obtained from AN-SOF is presented.
Modeling of Metallic Structures
Metallic structures can be modeled by combining different types of wires, grids, and surfaces:
Wires
Wire Grids and Solid Surfaces
- All types of curved wires can be modeled by means of arced or quadratic segments.
- Wire grids and solid surfaces can be defined using either curved or straight wire segments. Curved segments follow the exact curvature of discs, rings, cones, cylinders, spheres, and parabolic surfaces. Grids are composed of cylindrical wires that leave holes between them, while solid surfaces are composed of flat wires or strips that cover the surface without leaving holes between them.
- Tapered wires with stepped radii can be defined.
- All wires can be loaded or excited at any segment.
- The structure can also have finite non-zero resistivities (skin effect).
- Electrical connections of different wires and connections of several wires at one point are possible.
- Metallic wires in either dielectric or magnetic media can be analyzed.
- Wires with insulation can be modeled. Dielectric and magnetic coatings are available.
- The structures can be placed in free space, over a perfectly conducting ground plane or over an imperfect ground plane.
- Flat strip lines can be defined on a dielectric substrate for modeling planar antennas and printed circuit boards (PCB).
- Vias in microstrip antennas and printed circuit boards can also be modeled.
- The wire cross-section can either be Circular, Square, Flat, Elliptical, Rectangular or Triangular.
- Transmission lines can be connected to the metal structure. There are over 160 cable models available, including two-wire and coaxial cables, with characteristic impedance, velocity factor, and loss parameters adjusted to actual datasheets.
- The geometry modeling can be performed in suitable unit systems (um, cm, mm, m, in, ft). Different unit systems can also be chosen for inductance (pH, nH, uH, mH, H) and capacitance (pF, nF, uF, mF, F).
Excitation Methods
- Voltage sources can be placed on the wires, as many as there are segments, with equal or different amplitudes (RMS values) and phases.
- Current sources (e.g., representing impressed currents) can also be arranged at any segments.
- The voltage and current sources can have internal impedances.
- An incident plane wave of arbitrary polarization (linear, circular, or elliptical) and direction of incidence can also be used as the excitation.
- Hertzian electric and magnetic dipoles can also be modeled and used as the excitation.
- The antenna input power can be set to obtain the results (current distribution, near and far fields) scaled accordingly.
Frequency options
- The simulation can either be performed for a single frequency, for frequencies taken from a list or for a frequency sweep.
- The list of frequencies can either be created inside the program or loaded from a text file. It can also be saved to a txt file.
- Linear and logarithmic frequency sweeps are possible.
- A suitable unit system can be selected (Hz, KHz, MHz, GHz).
Data Input
- 3D CAD tools are implemented for drawing and modifying the structure geometry, including wires, grids, surfaces, discrete generators, and lumped loads.
- The segmentation of wire geometry can be done automatically or manually.
- Left-clicking on a wire selects and highlights it. Right-clicking on a wire reveals a pop-up menu with various options.
- Wire connections are easily established by copying and pasting the endpoints of wires.
- Special 3D symbols indicate the positions of sources, load elements, and ground points.
- All dialog boxes validate inputs for accuracy.
- The program includes mouse-supported functions for rotating, moving, and zooming.
- Transmission lines can be easily entered into a table, which serves as a library, for later use. A line is highlighted in the graphical interface for easy identification.
- The program allows you to import geometrical data from text files. It supports three different file formats for importing wires, including the NEC (Numerical Electromagnetics Code) cards. Additionally, it can import DXF files containing 3D LINE entities.
- The AN-SOF architecture integrates powerful numerical methods to achieve the fastest calculation speed and the most accurate results.
Data Output
- All computed data is stored in files for subsequent graphical analysis.
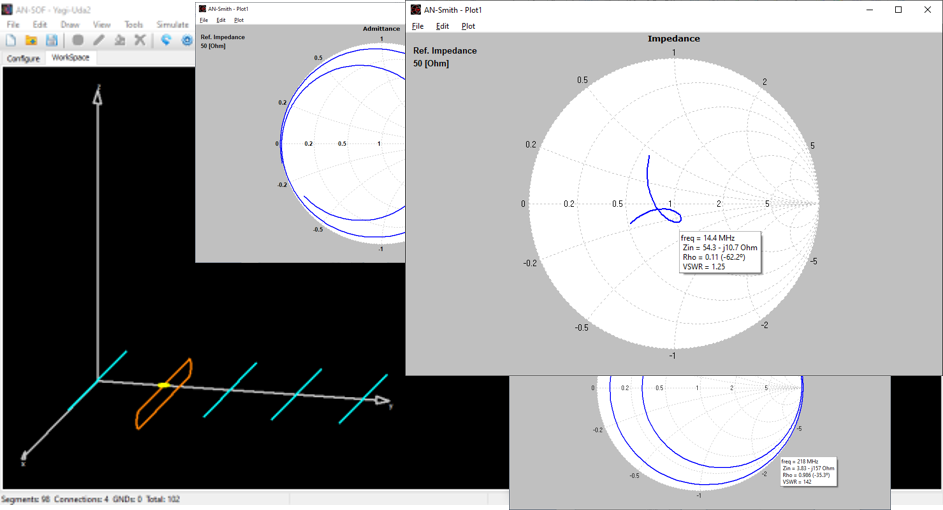
- Input impedances, currents, voltages, VSWR, S11, return and transmission losses, radiated and consumed powers, efficiency, directivity, gain, and other system responses are presented as lists in text format and can be plotted against frequency. A Smith chart is available to represent impedances and admittances, as well as to display the reflection coefficient and VSWR at the selected point on the graph.
- The current distribution on a selected wire can be plotted in amplitude, phase, real, and imaginary parts against position in a 2D representation. The currents flowing on a structure can also be plotted as a color map on the wires.
- Radiation and scattering fields are obtained, including power density, directivity and gain patterns, total electric field, linearly and circularly polarized components, axial ratio, and Radar Cross Section (RCS). The surface-wave field can be determined as a function of distance in the case of a real ground with finite conductivity.
- Near-field components can be calculated in Cartesian, cylindrical, and spherical coordinates. Field intensities can be plotted in 2D and 3D graphical representations and visualized as color maps in the proximity of a structure.
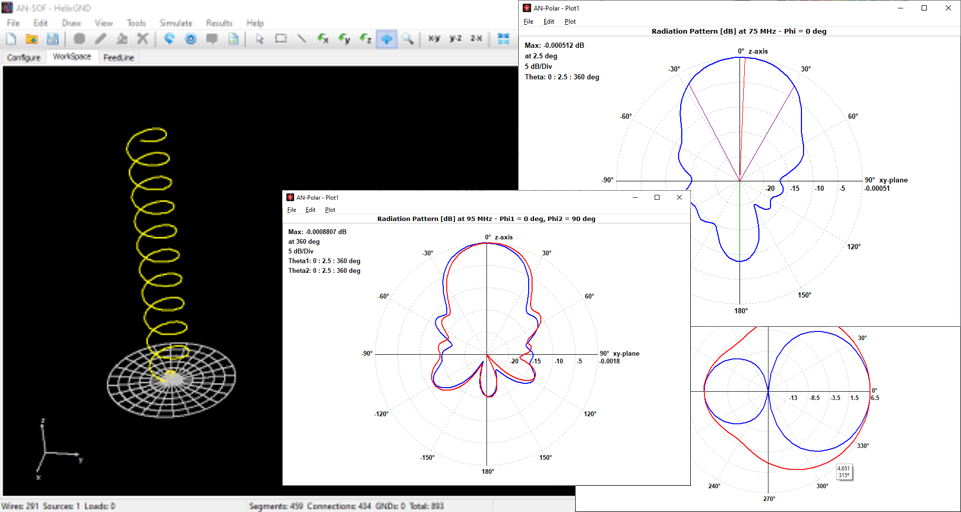
- A 2D representation of radiated fields is available in Cartesian and polar coordinates. The ARRL-style log scale can be applied to polar diagrams.
- 3D radiation patterns can be viewed from arbitrary angles with zoom functions, colored mesh and surface representations, and a color bar scale. 3D patterns can be plotted with specially designed lighting and illumination for enhanced visualization of simulation results.
- Far-field patterns can be separated into theta (vertical) and phi (horizontal) linearly polarized components, as well as right and left circularly polarized components. The axial ratio and the front-to-rear and front-to-back ratios are shown in polar plots and can be displayed as a function of frequency.
- The frequency spectrum of near- and far-fields can be visualized in a 2D representation for all field components across different frequencies.
- An average radiated power test, also known as AGT (Average Gain Test), is conducted to verify the accuracy of the simulation.
- The calculated data can be exported to .csv, .dat, or .txt files for use in other software programs.
- An embedded transmission line calculator is included to simplify the design of feed lines for transmitting antennas. Actual cable part numbers can be selected from a wide range of manufacturers, thanks to data extracted from cable datasheets and integrated into the calculator.
- A Bulk Simulation feature enables the automated calculation of multiple files, each with different geometric descriptions, to obtain results based on variable geometric parameters. The results are automatically exported to .csv files for further processing.
- You can choose suitable unit systems for the plotted results, including current scaling (KA, A, mA, uA), voltage scaling (KV, V, mV, uV), electric field scaling (KV/m, V/m, mV/m, uV/m), magnetic field scaling (KA/m, A/m, mA/m, uA/m), decibel scales, and more.
Integrated graphical tools
AN-SOF has a suite of integrated graphical tools for the convenient visualization of the simulation results. The following applications are installed automatically and used by the main program, AN-SOF:
AN-XY Chart app
A friendly 2D chart for plotting two related quantities, Y versus X. Use AN-XY Chart to plot parameters that depend on frequency, such as currents, voltages, impedances, reflection coefficient, VSWR, S11, radiated power, consumed power, directivity, gain, radiation efficiency, radar cross section, field components, axial ratio, and many more. Also plot the current distribution along wires as a function of position, 2D slices of radiation lobes and near fields as a function of distance from an antenna. Choose different units to display results and use the mouse to easily zoom and scroll graphs.
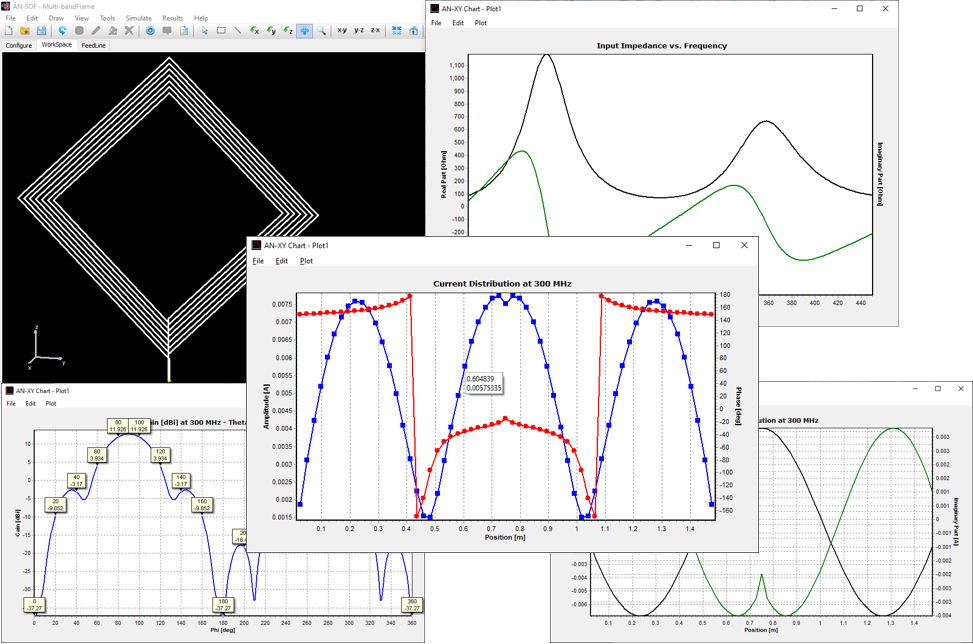

AN-Smith app
Plot impedance or admittance curves on the Smith chart with this tool. Just click on the graph to get the frequency, impedance, reflection coefficient, VSWR, and S11 that correspond to each point on the curve. Plots can be stored in independent files and opened later for a graphical analysis with AN-Smith.

AN-Polar app
Plot on a polar diagram the radiation pattern versus the azimuth (horizontal) or zenith (vertical) angles. The maximum, -3dB and minimum radiation levels are shown within the chart as well as the beamwidth and front-to-rear/back ratio. Click on the graph to quickly obtain the values of the radiated field. The represented quantities include power density, directivity, gain, normalized radiation pattern, total electric field, linearly and circularly polarized components, axial ratio, and radar cross section (RCS).

AN-3D Pattern app
Get a complete view of the radiation properties of a structure by plotting a 3D radiation pattern. AN-3D Pattern implements colored mesh and surface for the clear visualization of radiation lobes, including a color bar-scale indicating the field intensities over the lobes. Quickly rotate, move, and zoom the graph using the mouse. The 3D radiation pattern can be superimposed to the structure geometry to gain more insight into the directional properties of antennas.
The represented quantities include the power density, normalized radiation pattern, directivity, gain, total field, linearly and circularly polarized components, axial ratio, and Radar Cross Section (RCS). Choose between linear or decibel scales. Display near fields as color maps in the proximity of antennas in three different representations: Cartesian, cylindrical and spherical plots. Also plot the current distribution on the structure as a colored intensity map.
Main Window and Menu
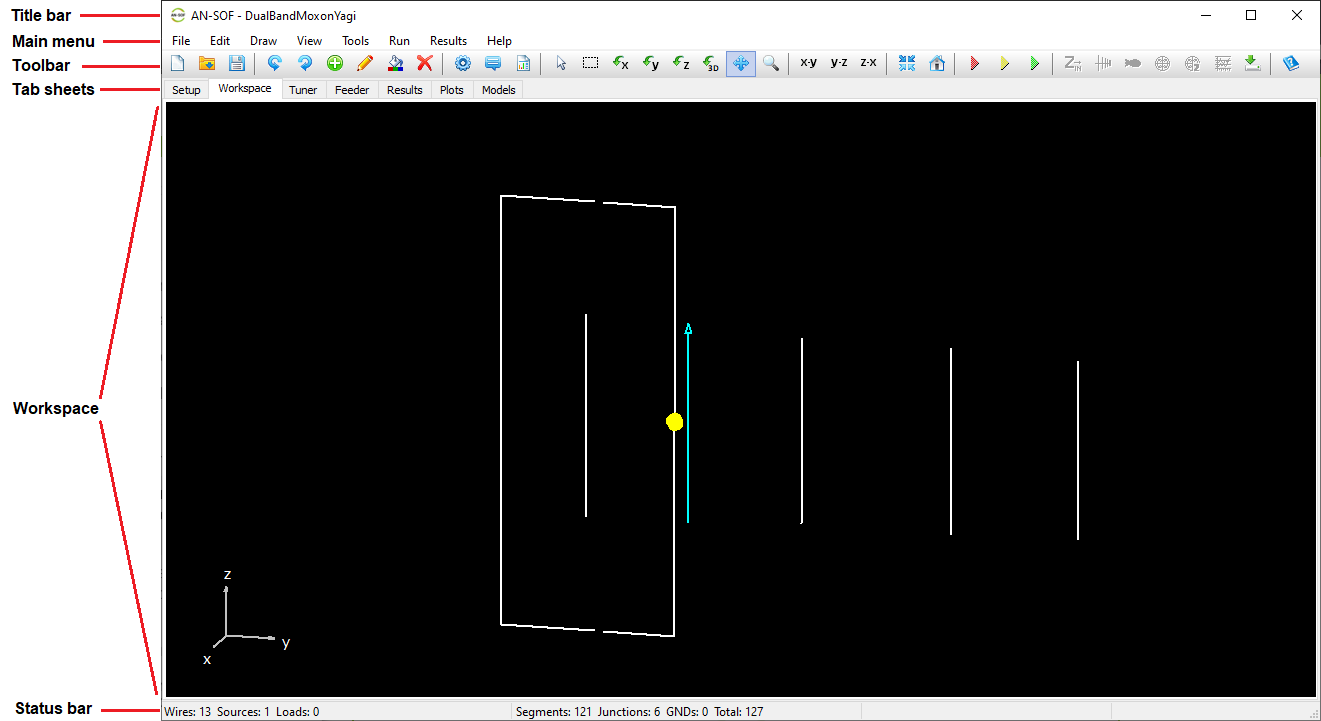
When AN-SOF starts, the main window displays several key components that form the core of the user interface (Fig. 1):
- Title Bar – Displays the name of the currently active project file (
.emmformat). - Main Menu Bar – Provides access to the primary menus: File, Edit, Draw, View, Tools, Run, Results, and Help.
- Toolbar – Contains icons for quick access to commonly used commands and tools.
- Tab Sheets – Allow users to switch between different stages of the workflow, from Setup to Plots, with a single click.
- Workspace – The central 3D canvas where wire structures are drawn and visualized.
- Status Bar – Displays real-time information, such as the number of segments, wire-to-wire junctions, and wire-to-ground connections (GNDs).
File Menu
The File menu provides commands for managing AN-SOF projects, including creating, opening, saving, importing, and exporting files. The available commands are:
- New… (Ctrl + N)
Creates a new project from scratch. - Open… (Ctrl + O)
Opens an existing project file (.emm) using the standard Open dialog. - Save (Ctrl + S)
Saves the current project under its existing name. - Save As…
Saves the current project with a new name. If the project is new, this command prompts the user to assign a name and location. - Import Wires
Opens a dialog to import wire data from various formats, including AN-SOF (.wre), NEC (.nec), and MM format (.txt). - Export Wires
Allows exporting the wire geometry to several formats:- NEC (
*.nec) - DXF (
*.dxf) - Scilab script (
*.sce) - MATLAB/Octave script (
*.m)
- NEC (
- Copy Workspace
Copies the current workspace view to the clipboard as a bitmap image. - Recent Files List
Displays up to ten recently opened project files for quick access. Use “Empty Recent Files List” to clear the history. - Exit (Ctrl + Q)
Closes the current project and exits AN-SOF.
Edit Menu
The Edit menu provides tools for modifying, organizing, and managing wires in your project. The available commands include:
- Undo (Ctrl + Z)
Reverts the project to the previous state before the last command was executed. - Redo (Ctrl + Y)
Reapplies the last undone action, restoring the project to the state before Undo was used. - Source / Load / TL (Ctrl + Ins)
Opens the Source/Load/TL toolbar, allowing you to add sources, loads, or connect transmission line (TL) ports to a selected wire segment. This command is enabled when a single wire is selected. - Modify (Ctrl + M)
Opens the Modify dialog box for editing properties of the selected wire(s). Available when one or more wires are selected. - Wire Color
Opens a standard color selection dialog to change the color of the selected wire(s). Enabled when one or more wires are selected. - Delete (Ctrl + Del)
Deletes the selected wire(s), including any attached sources or loads. Enabled when one or more wires are selected. - Copy Start Point
Copies the start point coordinates of the selected wire. This point can be used as the start of a new wire, enabling direct connection. Enabled when a wire is selected. - Copy End Point
Copies the end point coordinates of the selected wire for use as the starting point of a new, connected wire. Enabled when a wire is selected. - Start Point to GND
Draws a vertical wire from the start point of the selected wire down to the ground plane. This command is available only when a ground plane is defined in the model and a wire is selected. - End Point to GND
Draws a vertical wire from the end point of the selected wire down to the ground plane. Like the previous command, it is available when a ground plane exists and a wire is selected. - Move Wires… (Ctrl + Alt + M)
Opens the Move Wires dialog to reposition the selected wires. Enabled when at least one wire is selected. - Rotate Wires… (Ctrl + Alt + R)
Opens the Rotate Wires dialog to rotate selected wires around a specified axis. Enabled when at least one wire is selected. - Scale Wires… (Ctrl + Alt + S)
Opens the Scale Wires dialog to apply a scaling factor to the selected wires. Enabled when at least one wire is selected. - Copy Wires…
Opens the Copy Wires dialog to duplicate the selected wires, with options to apply translation or rotation to the copies. Enabled when at least one wire is selected. - Stack Wires…
Opens the Stack Wires dialog to generate multiple copies of the selected wires arranged along a specified direction. Enabled when at least one wire is selected.
Draw Menu
The Draw menu provides tools for creating a wide variety of wire geometries and wire grids. These commands allow users to model antenna elements with precision and flexibility. The available options include:
- Line
Opens the Line dialog box to draw a straight wire between two defined endpoints. - Arc
Opens the Arc dialog to draw a circular arc segment. - Circle
Opens the Circle dialog to draw a complete circular loop. - Helix
Opens the Helix dialog to create a helical wire, often used in axial-mode antennas. - Quadratic
Opens the Quadratic dialog to draw a curved wire defined by a quadratic function. - Archimedean Spiral
Opens the Archimedean Spiral dialog to draw a spiral with uniform spacing between turns. - Logarithmic Spiral
Opens the Logarithmic Spiral dialog to create a spiral with exponentially increasing spacing—ideal for frequency-independent antenna designs.
Wire Grid / Solid Surface
This option creates a wire grid or a discretized surface geometry. It includes the following sub-commands:
- Patch – Draws a rectangular mesh on the xy-plane.
- Plate – Creates a bilinear surface or flat panel.
- Disc – Draws a flat circular disc.
- Flat Ring – Draws a ring-shaped disc with a central hole.
- Cone – Creates a conical surface structure.
- Truncated Cone – Draws a cone with a flat top (cut-off cone).
- Cylinder – Draws a cylindrical surface.
- Sphere – Creates a spherical grid or surface.
- Paraboloid – Draws a parabolic reflector surface.
Tapered Wire
This option allows drawing wires with stepped-radius profiles, useful for simulating tapered elements such as monopoles or matching sections. Each command mirrors the standard wire options above (e.g., Line, Arc, Helix), but with the ability to assign different radii along the length.
- Tabular Input (Ctrl + T)
Opens a spreadsheet-style table for entering linear wires, sources, loads, and transmission lines numerically—ideal for precise control and batch input. - Transmission Lines (Ctrl + L)
Opens a dedicated table to define transmission lines by specifying their characteristic impedance, velocity factor, length, and loss parameters.
View Menu
The View menu provides options to control the display of interface elements, adjust zoom levels, and access additional project and wire information. Use these commands to customize your workspace and enhance your modeling experience:
- Wire Properties… (Ctrl + W)
Opens the Wire Properties dialog, showing detailed information about the selected wire. This command is available when a wire is selected. - Project Details…
Opens the Project Details dialog, displaying a summary of the current project, including the number of segments, wires, sources, and loads. - Zoom In (Ctrl + I)
Magnifies the view within the workspace. You can also zoom in by scrolling the mouse wheel backward. - Zoom Out (Ctrl + K)
Reduces the view scale in the workspace. You can also zoom out by scrolling the mouse wheel forward. - Reset Zoom Scale
Resets the zoom level and resizes the workspace to fit the entire structure. - Axes… (Ctrl + A)
Opens the Axes dialog to adjust the appearance of the coordinate axes. Press F7 to toggle between the small axes (shown in the lower-left corner) and the main axes (centered in the workspace). - X-Y Plane / Y-Z Plane / Z-X Plane
Switches the view to align the selected plane (XY, YZ, or ZX) parallel to the screen, offering easier modeling and inspection from different perspectives. - Center
Centers the view on the structure in the workspace without altering the zoom level. - Initial View (Home)
Resets the workspace to the default orientation and zoom level. - Drawing Panel
Displays a panel on the left side of the workspace with quick-access buttons for drawing wires, wire grids/solid surfaces, and tapered wires.
Tools Menu
The Tools menu provides access to plotting tools, wire checking utilities, and other helpful features for project analysis and customization. The commands available in this menu include:
- 3D Chart
Launches the AN-3D Pattern application to open and view 3D radiation pattern files (.p3d). - Polar Chart
Launches the AN-Polar application for displaying polar radiation patterns from.plrfiles. - Rectangular Chart
Launches the AN-XY Chart application to view rectangular (Cartesian) plots from.pltfiles. - Smith Chart
Launches the AN-Smith application to display impedance or reflection coefficient data from.sthfiles using a Smith chart. - Check Individual Wires
Verifies the segment length, cross-sectional size, and thin-wire ratio for each wire. Wires that fall outside acceptable ranges are highlighted in yellow (warning) or red (error). - Check Wire Spacing
Analyzes the spacing between adjacent wires to ensure they are sufficiently separated. Wires with spacing issues are also highlighted in yellow or red. - Delete Duplicate Wires
Automatically detects and removes duplicate or overlapping wires from the project. - RF Calculators
Opens a webpage with a collection of online tools for calculating antenna parameters, propagation metrics, component values, and unit conversions. - Calculator
Launches the built-in Microsoft Windows® Calculator for quick arithmetic operations. - Preferences…
Opens the Preferences dialog box, where users can configure unit systems, workspace appearance, pen width, confirmation prompts, and other interface settings.
Run Menu
The Run menu provides commands to execute the simulation of currents and electromagnetic fields. These options allow users to selectively perform calculations depending on their analysis needs:
- Run Currents and Far-Field (F10)
Calculates the current distribution on the wire structure, from which input impedance and VSWR are derived, along with the far-field radiation pattern, used to compute radiation efficiency, gain, and front-to-back ratio. - Run Currents and Near-Field (F11)
Calculates the current distribution and the near electric and magnetic fields around the antenna structure. - Run ALL (F12)
Executes a complete simulation including currents, far-field, and near-field calculations in a single step. - Run Currents (Ctrl + R)
Calculates only the current distribution on the wire structure.
This is useful when interested solely in input parameters (impedance, reflection coefficient, VSWR), avoiding the time cost of field computations.
Note: This command is disabled when the currents have already been computed. - Run Far-Field
Calculates the far-field radiation pattern based on previously computed currents.
Enabled only after the current distribution has been calculated. - Run Near E-Field
Computes the near electric field generated by the current distribution.
Requires prior current calculation. - Run Near H-Field
Computes the near magnetic field generated by the current distribution.
Requires prior current calculation. - Run Bulk Simulation
Opens a dialog to select multiple input files in NEC format (.nec). AN-SOF will import each file, run the simulation, and export the results as CSV files to the same directory. This is ideal for batch processing multiple designs.
Results Menu
The Results menu provides a set of commands for visualizing and exporting simulation results. These include current distributions, field patterns, power metrics, and spectral data. The available commands are as follows:
Plot Current Distribution
Launches the AN-3D Pattern application to visualize the current distribution as a color pattern mapped onto the wire structure.
Plot Currents
Opens the AN-XY Chart to plot the magnitude and phase of currents versus position along a selected wire. This command is enabled only when a wire is selected.
List Currents…
Displays the List Currents toolbar to show current values versus frequency at a specific segment on a selected wire. If the segment includes a source, additional data such as input impedance, voltage, and power versus frequency will also be available. This command is enabled only when a wire is selected.
Export Currents
Exports the current distribution along a wire to a CSV file, including position and frequency-dependent data. Enabled only when a wire is selected.
List Input Impedances…
Shows a table of input impedances versus frequency, including associated parameters such as reflection coefficient, VSWR, return loss, and transmission loss at the antenna terminals.
Plot Far-Field Pattern
Opens a sub-menu with commands for plotting the radiation pattern in various formats:
- 3D Plot: Launches AN-3D Pattern to visualize the full 3D far-field radiation pattern.
- Polar Plot 1 Slice: Opens a dialog to select a single 2D slice of the far-field pattern, displayed in polar coordinates using AN-Polar.
- Polar Plot 2 Slices: Allows selection of two 2D slices of the far-field pattern, displayed in polar coordinates using AN-Polar.
- 2D Rectangular Plot: Allows selection of a 2D slice of the far-field pattern, displayed in rectangular (Cartesian) coordinates using AN-XY Chart.
Plot Far-Field Spectrum
Opens a dialog to select a point in space where far-field components will be analyzed across frequency. The spectrum is displayed using AN-XY Chart.
List Far-Field Pattern
Displays a table of the total electric field and its components (E-theta, E-phi, right-hand and left-hand circular polarization) at the theta–phi angular grid defined in the Far-Field panel. The data can be exported as a CSV file.
List Far-Field Spectrum
Opens a dialog to select a spatial point where the far-field components will be listed versus frequency. The table includes the total E-field and its components: E-theta, E-phi, right-hand and left-hand polarized components. The data can be exported as a CSV file.
Power Budget / RCS
Displays the Power Budget dialog showing total input power, radiated and consumed power, power density, efficiency, directivity, and gain as functions of frequency. For simulations with plane wave excitation, the Radar Cross Section (RCS) versus frequency is shown.
Plot Near E-Field Pattern
Opens a sub-menu for near-field electric field visualization:
- 3D Plot: Launches AN-3D Pattern to show a 3D visualization of near E-field components.
- 2D Plot: Opens the Near-Field Cut dialog for selecting and plotting a 2D cut using AN-XY Chart.
Plot Near E-Field Spectrum
Opens a dialog to select a spatial point and plots the frequency response of the near E-field components using AN-XY Chart.
List Near E-Field Pattern
Displays a table of the total near electric field and its components at the grid defined in the Near-Field panel. The data can be exported as a CSV file.
List Near E-Field Spectrum
Opens a dialog to select a point in space and displays the near E-field spectrum in table format, including the individual field components versus frequency. The data can be exported as a CSV file.
Following these commands, similar options are available for Near H-Field and Power Density data. To compute power density, both the near E-field and H-field must have been previously calculated, as power density is obtained from the vector (cross) product of these fields at each spatial point.
Help Menu
Use the Help menu to access the user guide, technical support, license activation, and version information. This menu includes:
- User Guide
Opens the AN-SOF User Guide in PDF format. - AN-SOF Home Page
Opens the official website at www.antennasimulator.com in your default browser. - Knowledge Base
Opens the Knowledge Base where you can search categorized help articles and how-to guides. - Email to Tech Support
Launches your default email client to send a support request to info@antennasimulator.com. - Chat to Tech Support
Opens the live chat support page in your default browser. - Activate AN-SOF
Runs the AN-Key application, which shows your PC’s serial number and allows you to enter an activation key to license the software. - Check for Updates
Opens the webpage with the latest AN-SOF software releases. - About AN-SOF…
Displays version number, license, and copyright.
Main Toolbar
The main toolbar provides quick access to essential commands, many of which are also found in the main menu. In addition, it includes extra tools not available in the menu.
One such group consists of 3D View Controls, which help users interact with the 3D workspace (see Fig. 2):

3D View Controls
- Select Wire (arrow icon)
Activates selection mode. Click a wire to select it. To select multiple wires, hold Ctrl and click each one. Selected wires are highlighted in light blue. To deselect, Ctrl + click again, or double-click in the workspace or press ESC to clear all selections. - Selection Box
Allows selecting multiple wires by dragging a box with the left mouse button:- Drag from top to bottom to select only wires fully enclosed.
- Drag from bottom to top to select any wires that intersect the box.
- Previously selected wires will be deselected if included again.
- Double-click the workspace or press ESC to deselect all.
- Rotate around X/Y/Z
Rotates the view around the selected axis (X, Y, or Z) by moving the mouse in the workspace. - 3D Rotation
Enables free rotation around all axes by moving the mouse in the workspace. - Move (cross icon)
Pans the view by dragging the mouse with the left button held down. - Zoom (magnifying glass icon)
Lets you zoom into a selected area by dragging a rectangle. After zooming, use the mouse wheel to adjust the zoom level.
Other Toolbar Commands
- Export Results
Located next to the results-related buttons, this command exports the data in the Results tab to a CSV file.
Preferences
Preferences in AN-SOF allow users to customize the unit system for input and output data, adjust the workspace appearance, and configure various miscellaneous options. To access preferences, navigate to Tools > Preferences from the main menu.
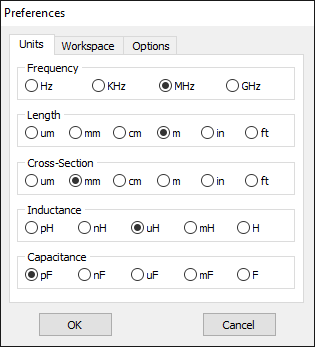
Units
On the Units page of the Preferences dialog box (see Fig. 1), users can select suitable units for frequencies, lengths, wire cross-section, inductances, and capacitances. Apart from standard SI units, options such as inches (in) and feet (ft) are available for lengths and cross-sections.
Workspace
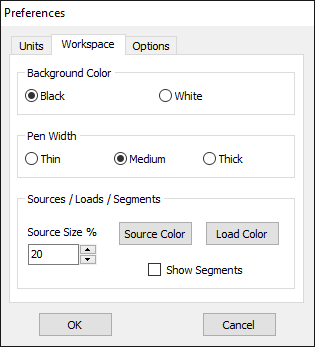
In the Workspace tab (Fig. 2), users can toggle the workspace background color between black and white. Additionally, there are three levels for the pen width used to draw objects on the workspace: Thin, Medium, and Thick. This option applies to axes, wires, and wire grids. Users can also customize the size and color of source symbols and loads. Enabling the Show Segments option displays the segments in the workspace.
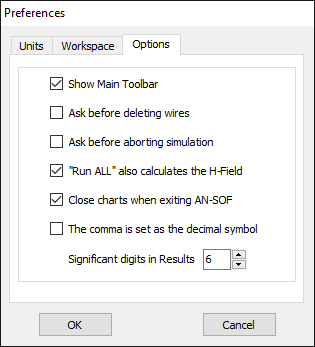
Options
In the Options tab, users can check the Show Main Toolbar option to display the toolbar (Fig. 3). Two “Ask before…” questions can be set to avoid mistakes. If the option “Run ALL” also calculates the H-Field is checked, the near H-field will be calculated after clicking on the “Run ALL” button. Users can also choose to close the chart windows after exiting AN-SOF. Additionally, the option “The comma is set as the decimal symbol” should be selected if the comma is used as the decimal separator in the Windows® regional settings. Users can also set the number of significant digits shown in results, although this option does not modify the double precision used in the internal algorithms.
Note
All preferences can be configured at any time, either before or after performing a calculation.
Display Options
The workspace background can be set to white or black. When a white (black) background is chosen, all wires will default to black (white) unless a different color is specified for specific wires. To set the workspace color, navigate to Tools > Preferences > Workspace tab. The color of selected wires can be changed at any time via Edit > Wire Color in the main menu.
The line width used for drawing wires and axes in the workspace can be adjusted by selecting a Pen Width option in the Workspace tab of the Preferences dialog box. There are three levels: Thin, Medium, and Thick. Figure 1 illustrates the different combinations of workspace color and pen width that can be achieved.
Viewing 3D Axes
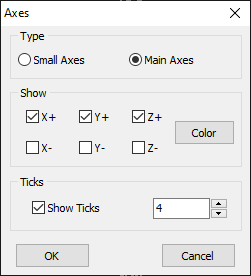
To customize the appearance of the X, Y, Z axes in the workspace, navigate to View > Axes (Ctrl + A) in the main menu to open the Axes dialog box (see Fig. 2). There are two types of axes:
- Small Axes: Displayed in the lower-left corner of the workspace.
- Main Axes: Displayed at the center of the screen.
Both positive and negative axes can be displayed. The color of the main axes can be changed by clicking the Color button. Check the Show Ticks option to add a specified number of ticks to the Main Axes.
Tip
Press F7 to switch between small and main axes.
Zooming the View
To zoom in or out of the structure in the workspace:
- Use the mouse wheel.
- On a laptop touchpad, use two fingers (similar to zooming an image).
- Alternatively, use the Zoom In (Ctrl + I) and Zoom Out (Ctrl + K) commands in the View menu.
For a more specific zoom on a particular area, click the Zoom button on the toolbar and drag a rectangle over the desired area. To return to the initial view, click the Initial View (Home) button on the toolbar.
Rotating the View
To rotate the view of the structure around a specific axis:
- Press one of the following toolbar buttons:
- Rotate around X
- Rotate around Y
- Rotate around Z
- 3D Rotation
- Move the mouse while holding the left button.
Alternatively, use the following keyboard shortcuts:
- F1: Right-handed rotation around the x-axis.
- F2: Left-handed rotation around the x-axis.
- F3: Right-handed rotation around the y-axis.
- F4: Left-handed rotation around the y-axis.
- F5: Right-handed rotation around the z-axis.
- F6: Left-handed rotation around the z-axis.
Moving the View
To move the view of the structure in the workspace:
- Click the Move button on the toolbar.
- Move the mouse while holding the left button.
Introduction
The Method of Moments (MoM) is widely recognized as one of the most reliable techniques for modeling and simulating antennas and radiating systems. However, traditional implementations of MoM suffer from several issues primarily stemming from approximations used in numerical calculations to reduce computational requirements. While these approximations were justified in the 1970s and 1980s due to limited processor speeds and memory capacities, the present-day computing power, even on personal computers, allows for more accurate calculations. The limitations imposed by these approximations in traditional MoM models restrict their validity and applicability.
The fundamental principle of MoM involves representing metal surfaces through wire segments, which is a suitable approximation for many metallic antennas, particularly wire-type antennas like linear antennas, dipoles, monopoles, yagis, log-periodic arrays, quads, antenna arrays of all types, traveling wave antennas, fractals, aperture antennas, and reflectors. It is essential for each wire segment to have a small length and cross-section relative to the wavelength. The MoM seeks to determine the unknown current flowing through each wire segment, as depicted in Fig. 1.
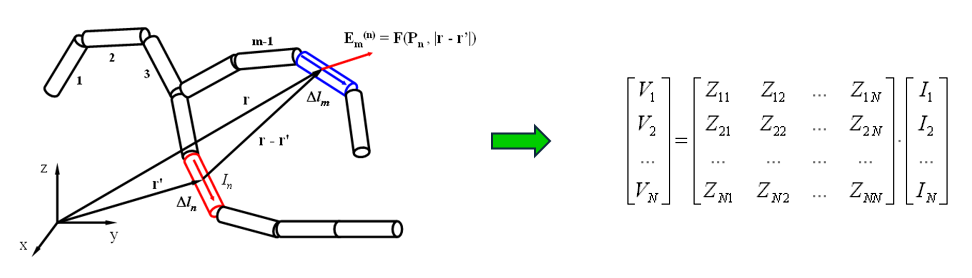
The Thin-Wire Approximation
In the modeling of antennas using cylindrical wire segments, the initial approximation commonly employed is known as the “thin-wire approximation,” as illustrated in Fig. 2. This approximation is based on the following assumptions:
- The electric current flowing through a wire can be represented as a filament along the wire axis, disregarding the fact that it actually flows on the wire’s surface.
- Variations in the current along the circular contour of the wire’s cross-section can be ignored.
- The component of the current perpendicular to the wire axis can be disregarded.
- It is sufficient to enforce the boundary condition of zero total tangential electric field on the surface of an ideal conducting wire along its axis.
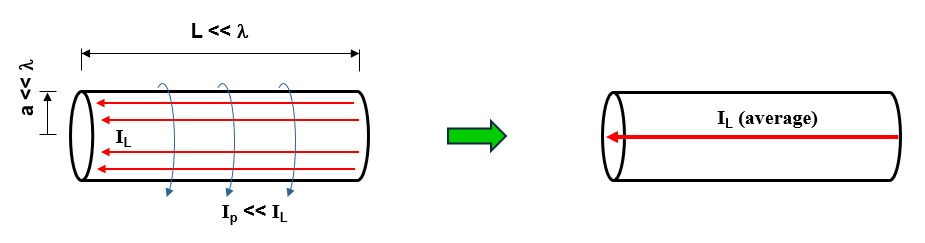
When dealing with a wire segment with a cross-section significantly smaller than the wavelength, assumptions 2, 3, and 4 are reasonably valid and align with experimental observations and theoretical predictions in the quasi-electrostatic regime for metal surfaces. However, assumption 1, regarding the current filament along the wire axis, has sparked debates throughout the history of linear antennas.
Assumption 1 only holds as a limiting case when the wire’s cross-section approaches zero size, such as when the wire has a circular cross-section and its radius tends to zero. This assumption relates to the crucial aspect known as the Kernel of the problem. The Kernel represents the core of the integral equation that the MoM solves to determine the currents flowing along the wires. Instead of employing the “thin-wire Kernel” utilized in traditional MoM, which is based on assumption 1, AN-SOF employs the exact Kernel. In the exact Kernel, it is considered that the current flows on the surface of the wires rather than being confined to a filament along the wire axis.
Eliminating assumption 1 has a significant impact on the accuracy of calculations, particularly in the current distribution near the antenna’s feed point or terminals, where obtaining precise values for input impedance and standing wave ratio (SWR) is crucial. In addition to discarding assumption 1 in AN-SOF, the use of the exact Kernel and curved wire segments helps overcome other issues inherent in traditional MoM, as described below.
Overcoming the 7 Limitations of the Traditional MoM
In AN-SOF, we have departed from the traditional MoM and embraced innovation by implementing a new method called the Conformal Method of Moments (CMoM) with an exact Kernel formulation. This decision stems from the lack of substantial improvements in traditional methods over several decades, despite advancements in computational power. By adopting CMoM with an exact Kernel, we have successfully addressed the main limitations of the traditional MoM, which can be categorized into seven key areas:
1. No curved wires:
Traditional MoM models rely on straight wire segments, which are suitable for linear antennas such as dipoles and their arrays. However, many antennas and structures have curved shapes. In traditional MoM, curved wires are approximated using a series of straight-line segments, leading to modeling errors that persist throughout the simulation. This approximation often produces inaccurate results for curved antennas like loops, helices, and spirals, particularly in terms of feed point impedances.
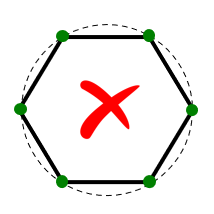
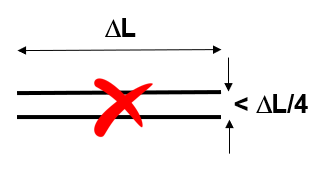
2. Wire spacing limitation:
Another limitation of traditional MoM is the spacing between parallel wires. Misleading results occur when the spacing between segments is less than a quarter of the segment length. As a result, the traditional MoM becomes less applicable when modeling configurations with close parallel wires, such as in two-wire transmission lines.
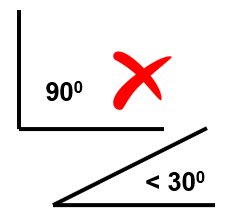
3. Issues with bent wires:
The thin-wire Kernel employed in traditional MoM leads to erratic numerical oscillations when wires are bent at right angles or have angles less than 30 degrees between adjacent segments.
4. Short segment constraint:
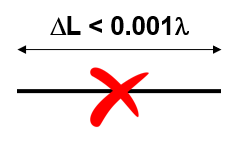
Traditional MoM imposes a constraint on the segment length, requiring it to be greater than 0.001 of a wavelength. Consequently, the traditional MoM cannot be effectively applied at very low frequencies. For instance, when modeling an electric circuit of around 1 meter operating at 60 Hz, the segment length needed to accurately represent the circuit becomes at least 5,000 times shorter than the minimum segment length supported by traditional MoM. Therefore, the traditional MoM implementation falls short when modeling wire antennas at low frequencies.
5. Thin wire requirement:
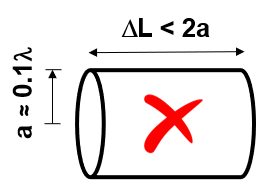
Thick wires deviate from the thin-wire approximation assumption, where current flow is limited to the wire axis rather than its surface. This deviation introduces significant errors in the results.
6. Tapered wire issues:
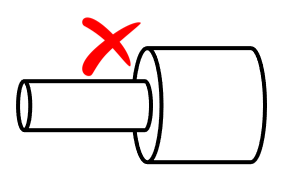
Changes in radius between adjacent segments create non-physical discontinuities in traditional MoM simulations.
7. Proximity to lossy ground plane affects horizontal wires:
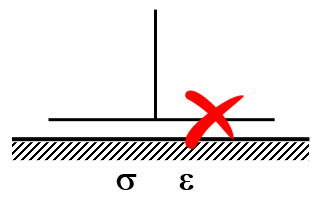
Antennas such as monopoles positioned above ground screens with elevated radial wires exhibit diverging input impedance and inaccurate antenna efficiency due to the influence of the lossy ground plane.
Thanks to the Conformal Method of Moments (CMoM) with Exact Kernel, AN-SOF has successfully eliminated these limitations. CMoM employs conformal segments that accurately capture the structure’s contour, enabling an exact representation of geometric details. Conformal segments, resembling curved cylindrical tubes, enable precise modeling of curved wires. By employing the exact Kernel instead of the thin-wire approximation, AN-SOF overcomes limitations associated with bent wires, small wire spacings, and segment lengths. This approach facilitates highly accurate calculations compared to the traditional method.
With the implementation of CMoM and an exact Kernel formulation, AN-SOF achieves enhanced accuracy, reduced computational requirements, and more efficient simulations. The improved method enables AN-SOF to simulate a wide frequency range, spanning from extremely low frequencies (e.g., 60 Hz circuits) to microwave antennas.
AN-SOF stands as the only antenna modeling software that offers a calculation engine based on the Conformal Method of Moments with an Exact Kernel.
Simulation Setup
Before drawing wires or running a simulation, it’s recommended to configure the simulation parameters in the Setup tab. This tab contains the following panels: Frequency, Environment, Far-Field, Near-Field, Excitation, and Settings (see Fig. 1).
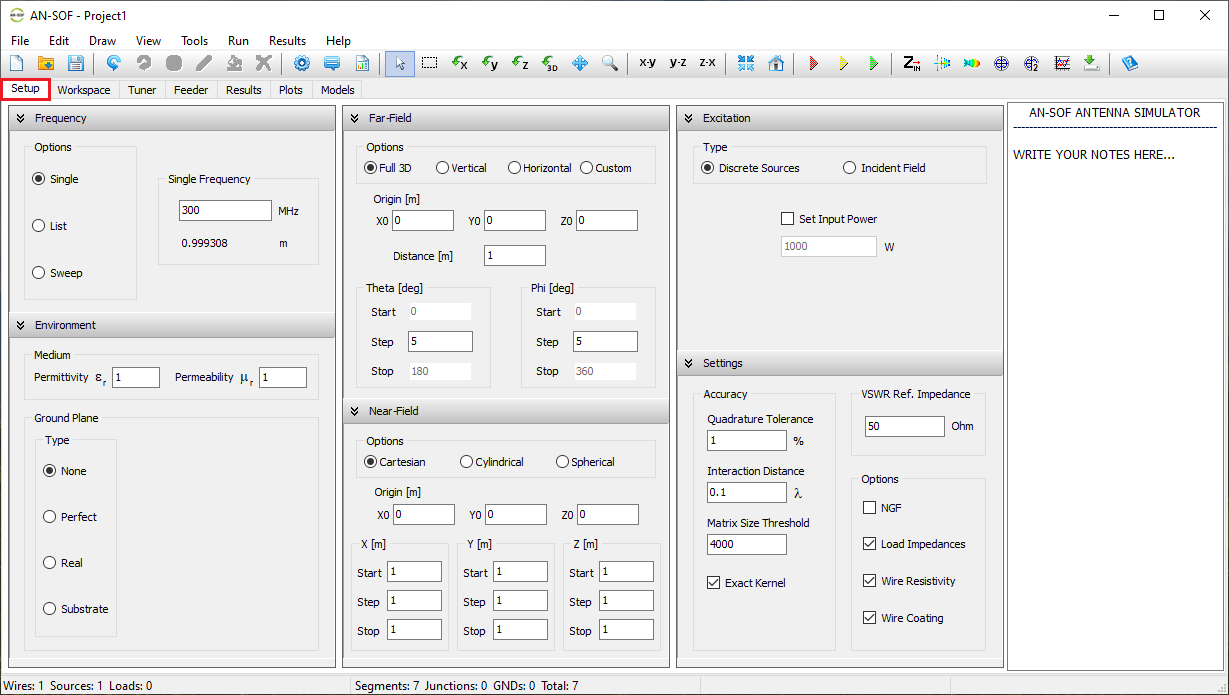
- Frequency panel: Specify the operating frequencies for the project.
- Environment panel: Set the relative permittivity and permeability of the surrounding medium, as well as the ground plane type.
- Far-Field panel: Define the angular ranges for far-field calculations.
- Near-Field panel: Define the observation points for near-field calculations.
- Excitation panel: Choose the excitation type for the structure. If using discrete sources, set the total input power. If using an incident field, define its direction and polarization.
- Settings panel: Set the reference impedance for VSWR and adjust parameters to fine-tune calculation accuracy.
Additionally, a Note panel on the right side of the Setup tab allows you to add project-related notes. These notes are saved in a .txt file in the same folder as the project file, using the same filename.
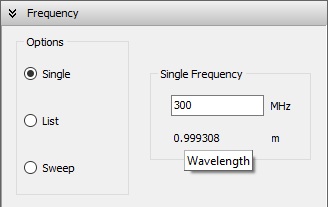
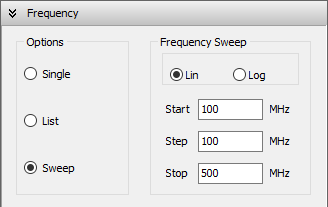
To define the operating frequencies, go to the Setup tab in the main window and select the Frequency panel. You can choose from three frequency modes: Single, List, or Sweep.
- Single: Enter a single frequency value in the Single Frequency box (see Fig. 1). The corresponding wavelength is displayed automatically below the frequency field.
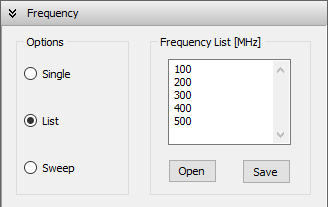
- List: Enter multiple frequencies in the Frequency List box (Fig. 2). You can import a list from a text file using the Open button, or export the current list using the Save button.
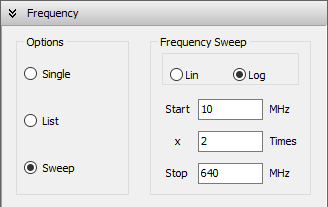
- Sweep: Perform a frequency sweep using either a linear or logarithmic scale.
- For a linear sweep, specify the start, step, and stop frequencies (Fig. 3).
- For a logarithmic sweep, enter the start and stop frequencies, along with a multiplication factor (Fig. 4).
To change the frequency unit (e.g., Hz, kHz, MHz, GHz), go to Tools > Preferences in the main menu, and select the desired unit on the Units page of the Preferences dialog box. See Preferences for more details.
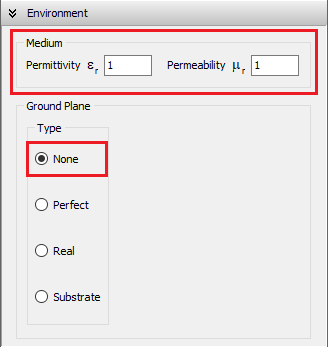
Environment and Ground Plane Options
The environment surrounding an antenna or metallic structure can be either free space or include a ground plane. In the case of free space, you can define the relative permittivity (dielectric constant εr) and magnetic permeability (µr) of the medium, with vacuum corresponding to εr = 1 and µr = 1.
Three ground plane options are available:
- Perfect Electric Conductor (PEC): An ideal, lossless ground plane.
- Real (Lossy) Ground: A ground plane with user-defined conductivity (σ) and relative permittivity (εr). Optionally, a radial ground screen can be added.
- Dielectric Substrate Slab: Used for modeling microstrip lines and printed antennas.
All ground planes lie in the xy-plane. The available environment settings will be described in detail in the sections below.
Configuring the Medium Properties
To configure the medium, navigate to the Setup tab > Environment panel. Use the Medium box (Fig. 1) to set the relative permittivity (εr) and permeability (µr) of the surrounding medium. When a ground plane is used, these values represent the permittivity and permeability of the medium above the ground.
Note:
The wavelength displayed below the frequency set in the Frequency panel (when the Single option is selected) and the wavelength used internally by AN-SOF for calculations will be adjusted based on the specified permittivity and permeability of the medium. Specifically, these properties cause the wavelength to shorten accordingly relative to the wavelength in a vacuum.
None (Free Space)
Selecting the None option simulates the antenna in free space. The relative permittivity (εᵣ) and permeability (µᵣ) specified in the Medium box (see Fig. 1) define the properties of the surrounding environment.
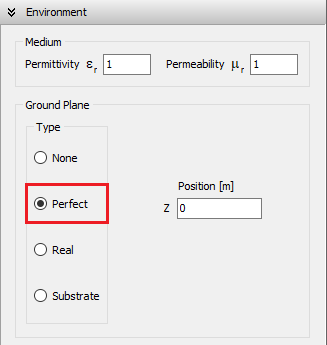
Perfect (PEC Ground)
Selecting the Perfect option places an infinitely large, perfectly electrically conducting (PEC) ground plane at a specified height relative to the xy-plane (see “Z Position” in Fig. 2). The ground plane remains parallel to the xy-plane, and its position is defined by the Z coordinate: a negative Z places the ground plane below the xy-plane, while a positive value places it above.
When using a perfect ground plane, all wires must be located above it—that is, each wire must have a Z-coordinate greater than or equal to the specified ground plane position. Wires crossing through or lying below the ground plane are not allowed. Additionally, horizontal wires placed directly on the ground plane are unsupported. However, connections from wire ends to the ground plane are permitted.
Real (Lossy Ground)
Selecting the Real option places a lossy ground plane at the xy-plane (z = 0), with user-defined conductivity (σ) and relative permittivity (εᵣ), as shown in Fig. 3. Four modeling methods are available for real ground calculations:
- Sommerfeld–Wait Asymptotic
- Reflection Coefficients
- Radial Wire Ground Screen
- Sommerfeld–Norton
These options are described in the following sections.
All wires must be positioned above the ground plane (z > 0). Horizontal wires directly on the ground plane are not supported.
Wire end connections to the ground are allowed when using either the Sommerfeld–Wait Asymptotic or Radial Wire Ground Screen options.
The Reflection Coefficients and Sommerfeld–Norton models assume perfect (zero-Ohm) wire connections to ground and yield reasonable results only for vertical wires connected to good conducting grounds—not dielectric surfaces. These models are not suitable when vertical wire-to-ground connections are made through dielectric materials.
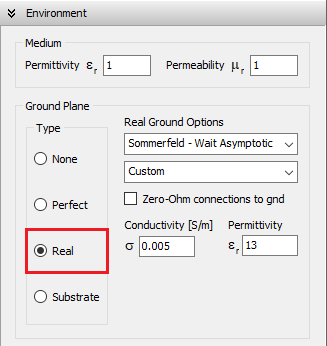
Real Ground: Sommerfeld – Wait Asymptotic
This option models the antenna/wire currents using a hybrid approach that combines a perfect ground plane with loss impedances to account for power dissipation in the real ground—particularly important when wires are close to or connected to the ground. Developed by Prof. James R. Wait, this model is especially effective for low-frequency (LF) and medium-frequency (MF) antennas, where ground conductivity tends to be high. However, it remains applicable at higher frequencies as long as the ground behaves as a good conductor.
The model uses the ground’s conductivity (σ) and permittivity (εᵣ) to compute both near-field and far-field radiation, applying Norton’s asymptotic approximations to the exact Sommerfeld solution. The far-field results match those predicted by Fresnel reflection coefficients.
Wire connections to ground are supported. If a wire’s starting or ending point is located at z = 0, it will automatically be connected to the ground. These connections are treated as imperfect (lossy) by default, meaning power can be dissipated at the connection point due to current flow. If the Zero-Ohm connections to ground option is enabled, these connections are instead treated as perfect (lossless), though the presence of the lossy ground still influences the overall near and far fields.
In summary, the Sommerfeld – Wait Asymptotic model is appropriate when the ground can be considered a good conductor at the operating frequency and when the structure includes wire-to-ground connections.
Real Ground: Reflection Coefficients
When this option is selected, the ground conductivity (σ) and relative permittivity (εᵣ) influence the current distribution on the antenna or wire structure above the ground. As a result, the input impedance of a transmitting antenna is also affected by real ground conditions. This influence is determined using a generalization of Fresnel’s reflection coefficients, which is theoretically valid when wires are positioned several wavelengths above the ground. In practice, however, good results have been reported for heights between one-quarter and one-half of a wavelength.
Near fields are calculated using Norton’s asymptotic approximations to Sommerfeld’s exact solution, allowing the electric and magnetic fields to be computed as a function of distance from the antenna. This enables analysis of field attenuation due to ground losses. The far field, by contrast, is computed using the standard Fresnel reflection coefficients.
Vertical wire connections to ground may be added when the ground behaves as a good conductor at the operating frequency, even though these connections theoretically violate the height requirement. These wire-to-ground connections are treated as lossless in this model.
In summary, the Reflection Coefficients ground model is best suited for wire structures located several wavelengths above ground, ideally without any wire-to-ground connections. However, if the ground is a good conductor at the operating frequency, vertical wire connections may be included—but results under such conditions should be interpreted with caution.
Real Ground: Radial Wire Ground Screen
When this option is selected, a ground screen made of buried radial wires is placed on the ground plane, which has the specified conductivity (σ) and relative permittivity (εᵣ). The screen is centered at the origin (0,0,0), and its configuration is defined by user-specified parameters: the number of radial wires, their length (or screen radius), and wire radius. These wires are assumed to be laid on the ground surface or buried at a depth less than one soil skin depth.
This model is based on Prof. James R. Wait’s theory for good conducting grounds. It affects the current distribution on the antenna or wire structure by accounting for the power dissipated in the combined ground plane and wire screen system. As a result, both the presence of the screen and the ground properties (conductivity and permittivity) influence the input impedance of a transmitting antenna located above the screen. The same parameters are used to compute the radiated near and far fields using Norton’s asymptotic approximations to Sommerfeld’s solution and Fresnel reflection coefficients, respectively.
Wire-to-ground connections may be defined at wire endpoints located at z = 0. These are treated as imperfect by default, meaning that power is dissipated in the ground-screen system due to currents flowing between the ground and the wires. If the Zero-Ohm connections to ground option is enabled, these connections are treated as perfect, with no power dissipation at the contact point.
In summary, the Radial Wire Ground Screen model is suitable when the ground behaves as a good conductor at the operating frequency and when the structure includes wire-to-ground connections. The screen serves to increase the effective conductivity of the combined ground-screen system, reducing power losses beneath antennas placed above it. Typical use cases include monopole antennas in the form of poles or radiating towers used in broadcasting applications.
Real Ground: Sommerfeld – Norton
Unlike the previous ground models, which apply various approximations to compute the current distribution on wires above a lossy ground plane, the Sommerfeld–Norton model numerically solves Sommerfeld’s exact solution. This enables simulations where the ground does not need to be a good conductor—it may instead be a dielectric medium. To approximate a purely dielectric ground, enter a very low conductivity (e.g., σ = 1E-6 S/m) along with the desired relative permittivity (εᵣ).
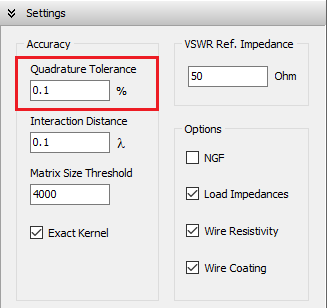
Vertical wires can be placed very close to the ground, with a minimum height of one wire radius above ground. Horizontal wires can be simulated as low as 0.005λ above ground. For vertical or horizontal wires at heights below 0.01λ, it is important to increase the accuracy of the calculations. To do this, go to Setup tab > Settings panel and set the Quadrature Tolerance to 0.1%, instead of the default 1% (see Fig. 4).
The near fields are computed from the current distribution using Norton’s asymptotic approximation to Sommerfeld’s solution. This is accurate at distances greater than about one-quarter wavelength from the wire structure, which is sufficient for most practical applications. The far field, in contrast, is calculated using Fresnel reflection coefficients, which yield the correct asymptotic expressions.
Wire-to-ground connections are theoretically not permitted in this model. However, they can be used with caution only for vertical wires, and only if the ground behaves as a good conductor at the operating frequency. In such cases, the model assumes lossless connections and employs specular reflection of the fields to compute the current distribution. These assumptions are valid only when the ground is effectively conductive.
In summary, the Sommerfeld–Norton model is the most accurate among the available ground models, but it comes with certain restrictions. It is recommended for highly dielectric grounds or situations where the ground cannot be considered a good conductor. Horizontal wires must not be placed below 0.005λ above ground. Vertical wires may be connected to ground only when the ground is a good conductor, and the results in such cases should be interpreted with care.
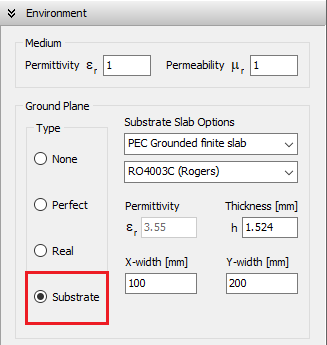
Substrate (Grounded Dielectric Slab)
When this option is selected, a dielectric substrate with user-defined relative permittivity (εᵣ) is placed beneath the xy-plane (z = 0), as shown in Figs. 5 and 6. The slab may extend infinitely or have finite dimensions in the xy-plane, where you can define its width along the X and Y directions. The substrate thickness, denoted as h, must also be specified. A perfectly electrically conducting (PEC) ground plane is located at z = –h, just below the dielectric slab (see Fig. 6). A drop-down list is available to select common substrate materials (e.g., FR4, RT/Duroid, Rogers RO). Note that the dielectric loss tangent cannot be specified—it is assumed to be zero, meaning the substrate is treated as lossless.
When the Substrate option is active:
- All wires must lie horizontally in the xy-plane (z = 0). These wires typically represent traces of printed antennas, microstrip lines, or PCB tracks.
- The only exception is for vertical wires (vias), which may connect traces at z = 0 to the ground plane at z = –h. These are commonly used to feed the structure with voltage or current sources.
Important constraints:
- The PEC ground plane beneath the substrate is mandatory and cannot be omitted. As a result, ungrounded dielectric substrates are not supported.
- Wires above the xy-plane (z > 0) or below the ground plane (z < –h) are not allowed in this model.
The Substrate model is an extension of the Conformal Method of Moments tailored for printed wire structures. It has the following limitations:
Model Limitations
Single-Layer, Lossless Substrate Only
- Only one dielectric layer is supported (multilayer stacks are not).
- The substrate must be lossless (loss tangent is assumed to be zero).
- No holes or cutouts are permitted in the substrate.
Finite-Size Substrate Constraints
- The substrate must be rectangular in shape.
- Traces must be placed at least 5× their width away from the substrate edges.
Ground Plane and Vias
- A PEC ground plane is always present and cannot be disabled.
- Vertical wires (vias) can be added to connect traces to the ground, typically for feeding.
No Slot-Based Designs
- Slot antennas or patches with slots cannot be modeled due to software limitations.
To configure radiation pattern parameters, navigate to the Setup tab in the main window and select the Far-Field panel (Fig. 1).
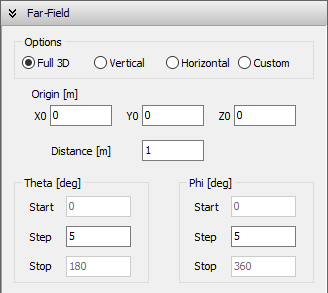
The far field can be computed after calculating the current distribution. Thus, the parameters set in the Far-Field panel have no effect on the determination of the currents and can be modified at any time. However, the far field must be recalculated every time these parameters are modified.
There are four options for radiation pattern calculations:
Full 3D
The far field is calculated in angular ranges that cover the entire 3D space, allowing you to obtain 3D radiation lobes. The steps for the Theta (zenith) and Phi (azimuth) angles can be set in the Theta [deg] and Phi [deg] boxes.
Vertical
The far field is calculated at a vertical slice for a given Phi (azimuth) angle. The step for the Theta (zenith) angle can be set in the Theta [deg] box, while the fixed Phi can be set in the Phi [deg] box.
Horizontal
The far field is calculated at a horizontal slice for a given Theta (zenith) angle. The step for the Phi (azimuth) angle can be set in the Phi [deg] box, while the fixed Theta can be set in the Theta [deg] box.
Custom
The far field is calculated for the specified ranges of angles Theta (zenith) and Phi (azimuth). The start, step, and stop values for Theta and Phi can be set in the Theta [deg] and Phi [deg] boxes.
Additionally, the following parameters can be set:
Origin (X0,Y0,Z0)
This is any point used as a phase reference. Its coordinates do not affect the shape of the radiation pattern. The 3D radiation pattern will be plotted centered at this point.
Distance
This represents the distance from (X0,Y0,Z0) to an observation point in the far-field region. A normalized far-field pattern can be obtained by setting Distance = 1 meter.
The zenith and azimuth angles, Theta (θ) and Phi (ɸ), are shown in Fig. 2. The figure also illustrates the Distance R from the structure to an observation point in the far-field zone. These three numbers (R, θ, ɸ) define the spherical coordinates of the far-field point.
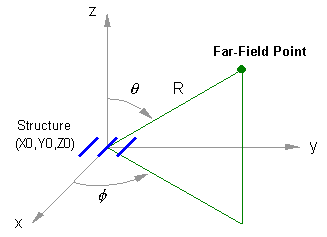
A frequently asked question is how to displace the center of the radiation pattern in a 3D plot displaying the radiation lobes. The answer lies in setting the Origin (X0, Y0, Z0) in the Far-Field panel. This allows you to adjust the reference point for the radiation pattern, enabling better visualization of the results. For more details, refer to this article:
To configure the observation points for the calculation of near fields, navigate to the Setup tab in the main window and select the Near-Field panel.
The near field can be computed after calculating the current distribution. Thus, the parameters set in the Near-Field panel have no effect on the determination of the currents and can be adjusted at any time. However, the near field must be recalculated whenever these parameters are modified.
The Near-Field panel provides three coordinate system options for near-field calculations:
- Cartesian
- Cylindrical
- Spherical
By selecting one of these options, near fields can be calculated in Cartesian, Cylindrical, or Spherical coordinates, depending on your preference or the requirements of your analysis.
Cartesian Coordinates
If the Cartesian option is selected, the following parameters can be configured for near-field calculations (Fig. 1):
Origin (X0, Y0, Z0)
This is the origin of the Cartesian coordinate system used to define the observation points where near fields will be calculated.
X
This box is used to specify the x-coordinates of the observation points where near fields will be calculated. You must set the start, step, and stop values for the x-coordinates. The start and stop values are measured relative to X0.
Y
This box is used to specify the y-coordinates of the observation points where near fields will be calculated. You must set the start, step, and stop values for the y-coordinates. The start and stop values are measured relative to Y0.
Z
This box is used to specify the z-coordinates of the observation points where near fields will be calculated. You must set the start, step, and stop values for the z-coordinates. The start and stop values are measured relative to Z0.
Cylindrical Coordinates
If the Cylindrical option is selected, the following parameters can be configured for near-field calculations (Fig. 2):
Origin (X0, Y0, Z0)
This is the origin of the cylindrical coordinate system used to define the observation points where near fields will be calculated.
R
This box is used to specify the radial distances (R-coordinates) of the observation points where near fields will be calculated. You must set the start, step, and stop values for the radial distances. The start and stop distances are measured relative to the origin (X0, Y0, Z0).
Phi
This box is used to specify the azimuth angles (phi-coordinates) of the observation points where near fields will be calculated. You must set the start, step, and stop values for the azimuth angles in degrees.
Z
This box is used to specify the z-coordinates of the observation points where near fields will be calculated. You must set the start, step, and stop values for the z-coordinates.
Spherical Coordinates
If the Spherical option is selected, the following parameters can be configured for near-field calculations (Fig. 3):
Origin (X0, Y0, Z0)
This is the origin of the spherical coordinate system used to define the observation points where near fields will be calculated.
R
This box is used to specify the radial distances (R-coordinates) of the observation points where near fields will be calculated. You must set the start, step, and stop values for the radial distances. The start and stop distances are measured relative to the origin (X0, Y0, Z0).
Theta
This box is used to specify the zenith angles (theta-coordinates) of the observation points where near fields will be calculated. You must set the start, step, and stop values for the zenith angles in degrees.
Phi
This box is used to specify the azimuth angles (phi-coordinates) of the observation points where near fields will be calculated. You must set the start, step, and stop values for the azimuth angles in degrees.
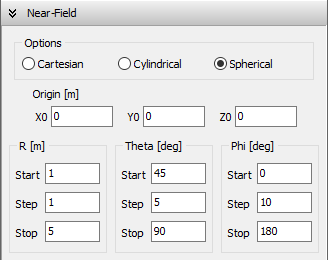
Near-Field Calculation Workflow
The Cartesian, Cylindrical, and Spherical options described above define a grid of observation points where the near field will be computed. The near electric field (E-field) and near magnetic field (H-field) can be calculated separately, or you can compute them sequentially by clicking Run Currents and Near-Field (F11) in the Run menu or toolbar. This command first calculates the current distribution and then computes the near fields.
Alternatively, the calculation of the current distribution, far-field, and near-field can be executed in a single step by selecting the Run ALL (F12) command in the Run menu.
If the near H-field is not required, you can disable its automatic calculation by turning off the “Run ALL also calculates the H-Field” option. This setting can be found in the Options tab of the Preferences window. To access the Preferences window, click the gear button in the main toolbar or navigate to Tools > Preferences in the main menu.
⚠ Note:
When defining the grid of points for near-field calculations, the closest distance from a near-field point to a wire with a circular cross section must be at least five times the wire radius. For flat strip conductors (such as those used in metallic surfaces), the near-field point must be located at a distance of at least one strip width from the strip.
Accessing Excitation Settings
Navigate to:
Setup tab > Excitation panel
Two excitation types available (Fig. 1):
- Discrete Sources
- Incident Field
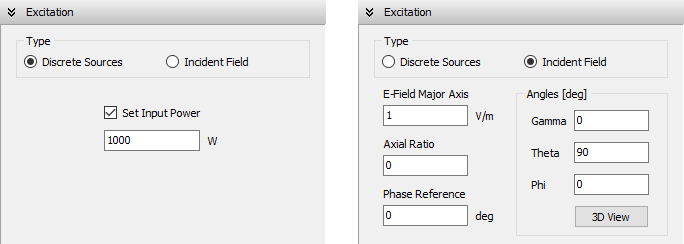
Discrete Sources
- Purpose: Calculate current distribution using voltage/current sources on wires
- Power Configuration:
- Specified Input Power: Sources auto-adjust to achieve target power (Watts)
- Unspecified Power: Sources remain constant; power becomes output result
Incident Field (Plane Wave Excitation)
Define an incident plane wave’s direction and polarization:
Key Parameters
| Parameter | Description | Units/Values |
|---|---|---|
| E-Field Major Axis | Linear: RMS amplitude (V/m) Elliptical: Major axis of polarization ellipse | V/m |
| Axial Ratio | Minor/major axis ratio: – Positive: Right-handed ellipse – Negative: Left-handed ellipse – Zero: Linear polarization | Unitless |
| Phase Reference | Phase shift at coordinate origin | Degrees |
| Gamma | Linear: Polarization angle from incidence plane Elliptical: Major axis angle from incidence plane | Degrees |
| Theta | Zenith angle of incidence | Degrees |
| Phi | Azimuth angle of incidence | Degrees |
3D Visualization
Click 3D View (Fig. 3) to interactively set:
- Wave direction
- Polarization state
Note
When an incident plane wave is used as the excitation, any discrete sources present will be ignored during the simulation.
Note
When an incident plane wave is used as the excitation, the calculated far-field and near-field results represent the scattered fields. The resulting radiation pattern is the scattered field pattern, observed in the far-field region where the scattered field amplitude decays with the inverse of the distance (1/r), and the scattered power density decays with the inverse square of the distance (1/r²) from the structure.
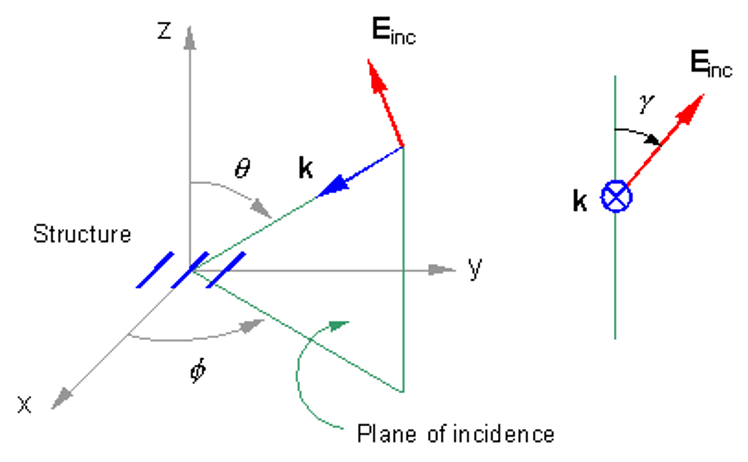
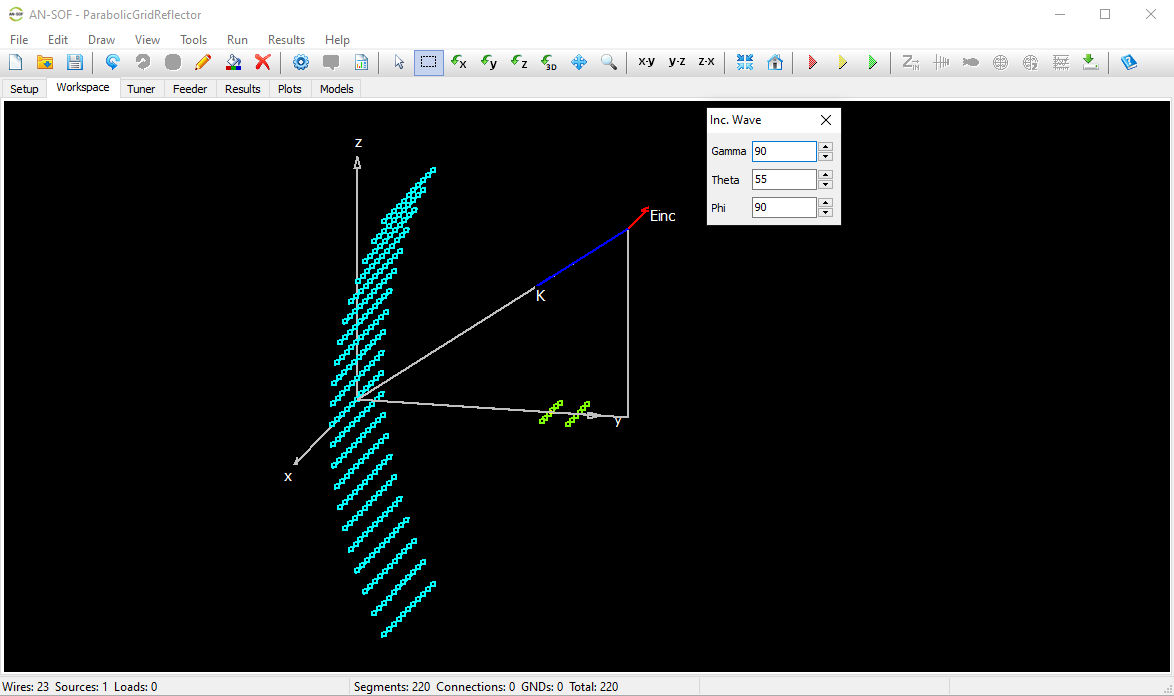
To access advanced simulation options, go to the Setup tab and select the Settings panel. Here, you can:
- Fine-tune the accuracy of the simulation,
- Set the reference impedance for VSWR calculations, and
- Adjust various options that affect the calculation engine.
These settings provide greater control over simulation precision and convergence behavior. See Fig. 1.
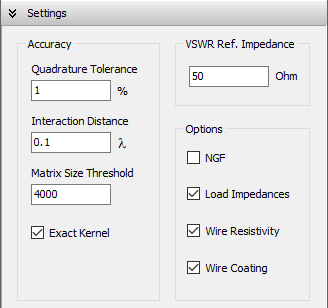
Controlling Numerical Precision
The Accuracy section in the Settings panel allows you to control the precision of the simulation and manage memory usage for large models.
- Quadrature Tolerance defines the acceptable numerical error in the evaluation of integrals between wire segments that are closer than the Interaction Distance. This parameter governs the precision of electromagnetic interaction calculations. The default value is 1%.
- Interaction Distance sets the maximum separation (in wavelengths) between segments for which the numerical integration guarantees an error below the Quadrature Tolerance. For segments farther apart than this distance, a third-degree polynomial approximation is used instead of the traditional Hertzian dipole approximation, offering improved accuracy for curved segments. The default value is 0.1λ.
- Matrix Size Threshold determines the maximum size of the impedance matrix (N × N, where N is the number of wire segments) that is computed in double precision. For models with more segments than the set threshold, single precision is used to reduce memory usage. While this may slightly reduce accuracy, it enables the simulation of larger models on systems with limited Windows on-board memory. The default threshold is 4,000.
- Exact Kernel enables the use of the exact formulation of the Electric Field Integral Equation (EFIE), significantly improving accuracy for antennas made with thicker wire segments. When this option is disabled, an extended thin-wire approximation is used. See The Exact Kernel for more information.
VSWR Reference Impedance Configuration
The reference impedance serves as the normalization value for VSWR calculations throughout the simulation. This parameter is particularly important when matching simulation conditions to real-world measurement setups.
Key features:
- Defaults to 50 Ω (standard for most RF systems)
- Commonly adjusted to 75 Ω for television/video applications
- Requires refreshing the results (Ctrl + R) to update all VSWR-dependent data
Simulation Control Options
These global toggles enable efficient comparison of different simulation scenarios without modifying individual element properties. They are especially valuable for parametric studies and troubleshooting.
| Option | Technical Implementation | Practical Application |
|---|---|---|
| NGF | Stores LU-decomposed impedance matrix after first calculation | Accelerates repeated simulations with varying source excitations |
| Load Impedances | Master switch for all lumped load elements in the model | Quickly compare loaded vs. unloaded system performance |
| Wire Resistivity | Toggles Ohmic loss calculation for all conductors | Evaluate conductor loss impact on system efficiency |
| Wire Coating | Enables/disables dielectric coating effects | Analyze insulation impact on antenna performance |
Implementation Note:
These options provide non-destructive alternatives to physically removing/readding model elements when running comparative analyses.
A summary of the project information can be displayed by navigating to View > Project Details in the main menu. This opens the Project Details window (Fig. 1). Alternatively, you can access this window using the dedicated button on the toolbar.
The text in the Project Details window can be selected and copied to the clipboard in the usual way (Ctrl + C to copy from the window and Ctrl + V to paste elsewhere).
The Project Details window provides a comprehensive summary of the following project information:
- Project Name: The name of the project.
- Date and Time: The date and time when the project was last saved.
- Structure: Includes the number of wires, sources, loads, transmission lines, and segment counts.
- Excitation: Indicates whether discrete sources or an incident field are set.
- Frequencies: Displays the frequency range configured for the simulation.
- Medium: Lists the permittivity, permeability, and wavelength (of the upper medium if a ground plane is present).
- Ground Plane: Specifies the type of ground plane and its associated parameters, if applicable.
- Far-Field Parameters: Displays settings related to far-field calculations.
- Near-Field Parameters: Shows settings for near-field calculations.
- Numerical Accuracy: Provides details about the settings employed for numerical accuracy.
- Units: Lists the units used for frequency, length, wire radius, inductance, and capacitance.
When a project is saved in AN-SOF, multiple files that share the same name as the project are saved within the same directory. Each file has a unique extension that corresponds to its specific content.
IMPORTANT: When requesting support, please compress all the project files into a ZIP archive and attach it to your support request email.
These files include:
| File type | Description |
|---|---|
| *.emm | Main file with configuration data |
| *.wre | Geometric description of the wire structure |
| *.cur | Current distribution |
| *.phi | E-phi component of the far-field. |
| *.the | E-theta component of the far-field. |
| *.pwr | Radiation pattern data |
| *.nef | Near electric field |
| *.nhf | Near magnetic field |
| *.ngf | Numerical Green’s function |
| *.txt | Notes written by the user |
Pressing ALT with the underlined letter of a menu item will execute the command associated with the item.
The following keys and associated actions are available:
| Key | Action |
|---|---|
| Home | Return the structure to the initial view |
| ESC | Deselect all wires |
| F1 | Rotate view around +X axis |
| F2 | Rotate view around -X axis |
| F3 | Rotate view around +Y axis |
| F4 | Rotate view around -Y axis |
| F5 | Rotate view around +Z axis |
| F6 | Rotate view around -Z axis |
| F7 | Show/hide main and small axes |
| F8 | Select a wire in order of creation |
| F9 | Select a wire in reverse order of creation |
| F10 | Run current distribution and far-field |
| F11 | Run current distribution and near-field |
| F12 | Run full simulation (all options) |
| Ctrl + A | Open Axes dialog box |
| Ctrl + I | Zoom in |
| Ctrl + K | Zoom out |
| Ctrl + L | Open Transmission Lines dialog |
| Ctrl + M | Modify selected wire(s) |
| Ctrl + N | Create a new project |
| Ctrl + O | Open an existing project |
| Ctrl + Q | Exit AN-SOF |
| Ctrl + R | Run current distribution only |
| Ctrl + S | Save the project |
| Ctrl + T | Open tabular input for linear wires |
| Ctrl + W | Show properties of selected wire |
| Ctrl + Y | Redo |
| Ctrl + Z | Undo |
| Ctrl + Del | Delete selected wire(s) |
| Ctrl + Ins | Show Source/Load/TL toolbar |
| Ctrl + Alt + M | Move selected wire(s) |
| Ctrl + Alt + R | Rotate selected wire(s) |
| Ctrl + Alt + S | Scale selected wire(s) |
Drawing Wires
AN-SOF provides several wire types for creating antenna geometries. Each wire type has its own geometric parameters, attributes, and material settings, which can be configured through a dedicated Draw dialog box. This dialog box allows you to insert and customize new wires directly in the workspace.
Selecting Draw from the main menu displays the following wire types:
- Line – Opens the dialog box for drawing a straight (linear) wire.
- Arc – Opens the dialog box for drawing a circular arc.
- Circle – Opens the dialog box for drawing a circular loop.
- Helix – Opens the dialog box for drawing a helical wire.
- Quadratic – Opens the dialog box for drawing a wire following a quadratic curve.
- Archimedean Spiral – Opens the dialog box for drawing an Archimedean spiral.
- Logarithmic Spiral – Opens the dialog box for drawing a logarithmic spiral.
Accessing Drawing Commands
The wire drawing tools can be accessed through any of the following:
- Main Menu → Draw
- Right-click Menu – Right-click on the workspace to open the context menu
- Main Menu → View → Drawing Panel (see Fig. 1)
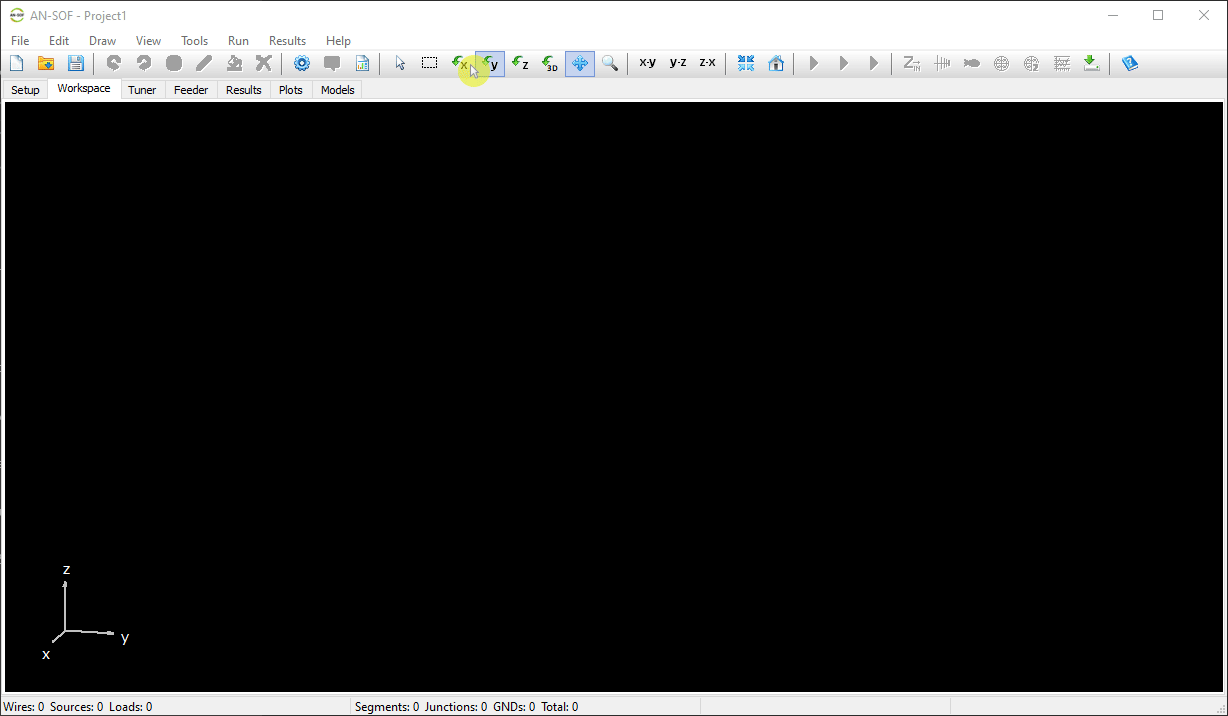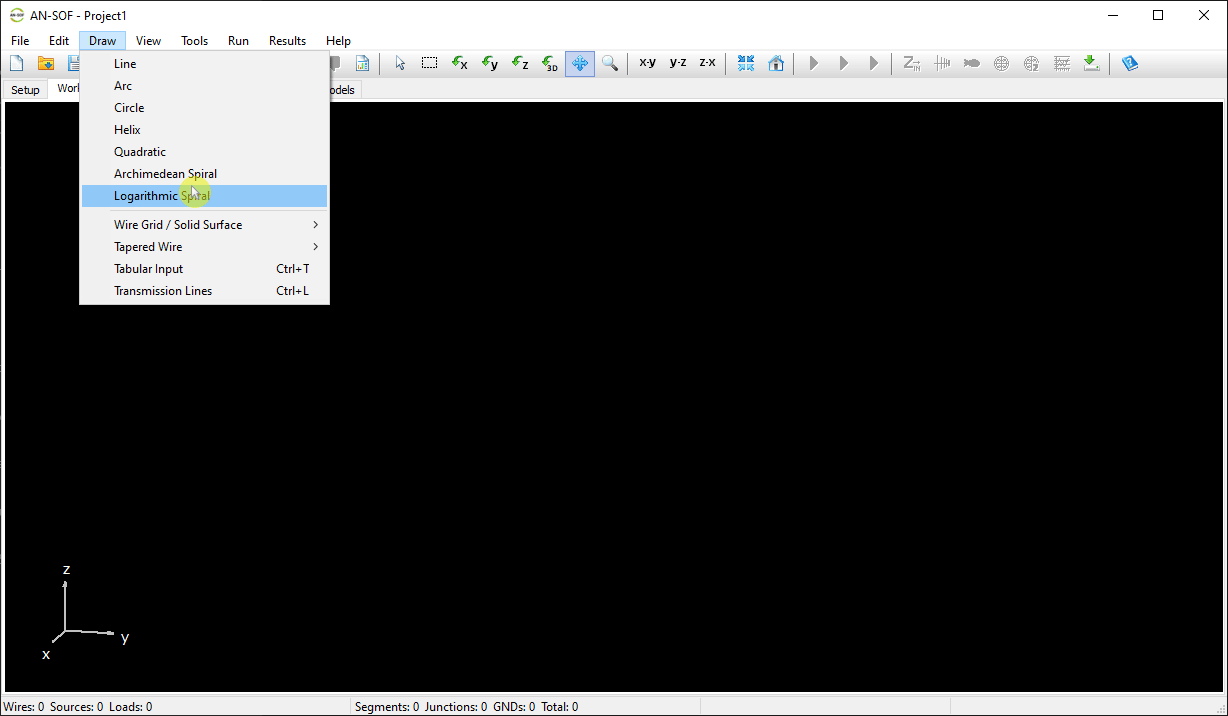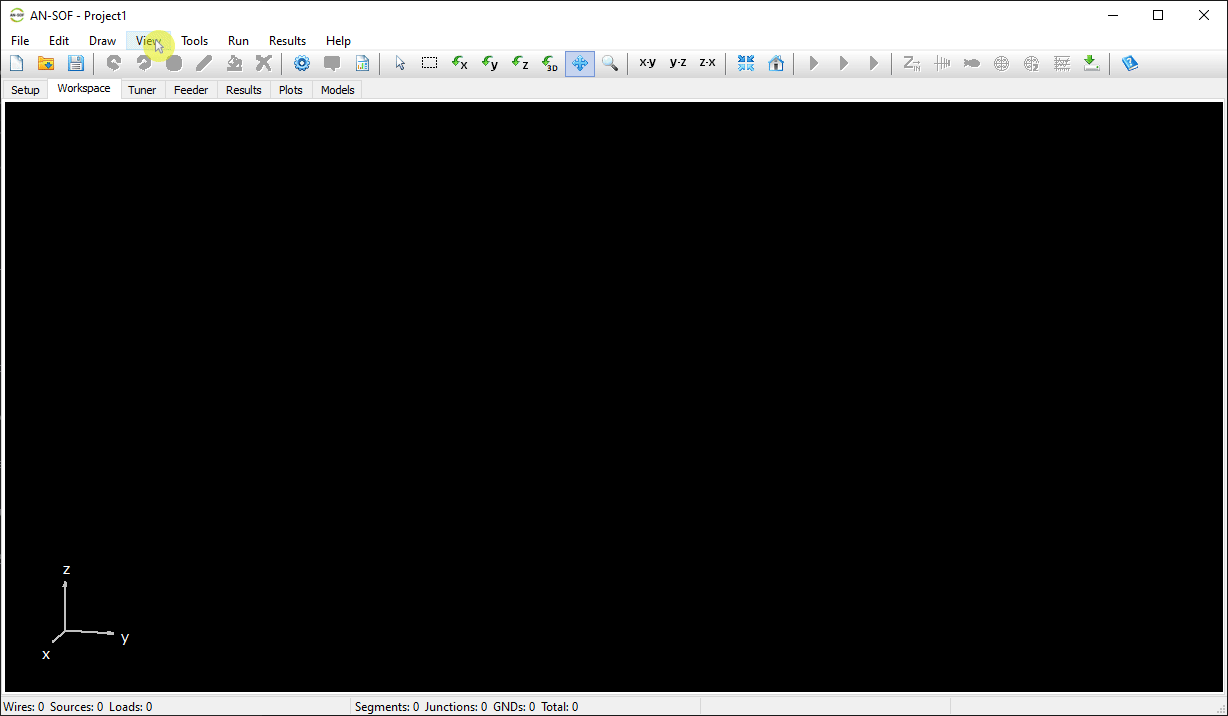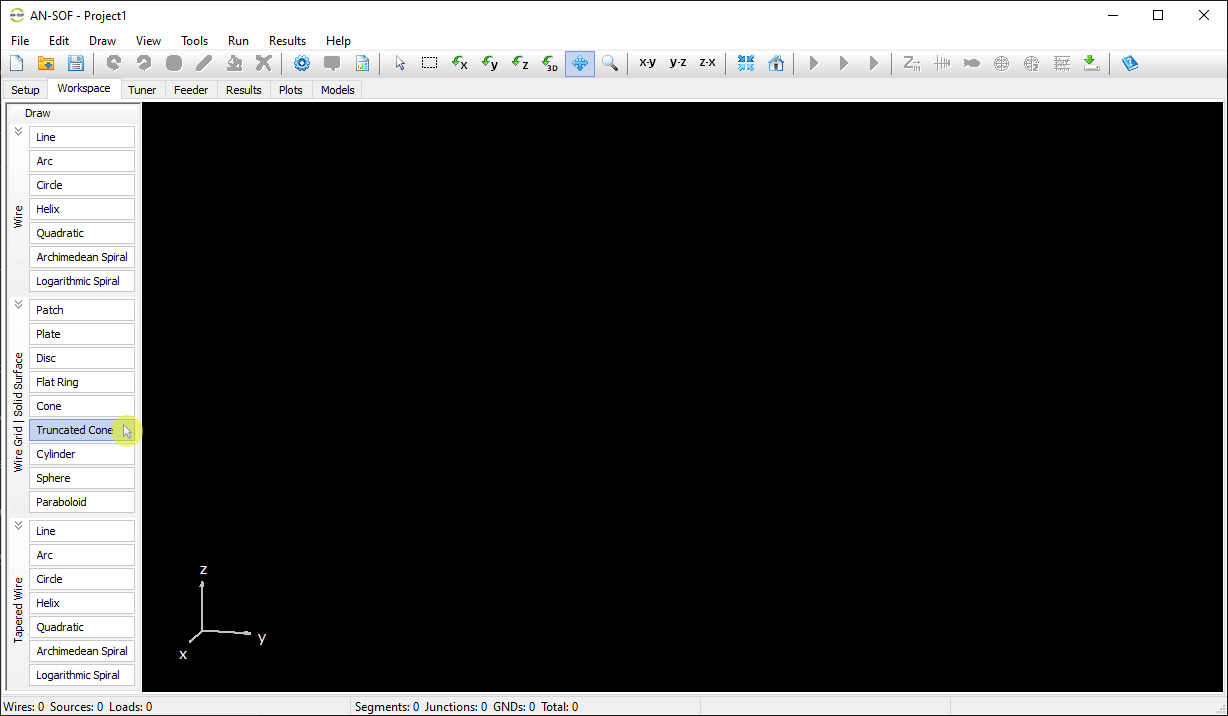
The Attributes page is part of the Draw dialog box for the selected wire type (see Fig. 1). On the Attributes page, you can specify the following attributes:
Number of Segments
Every wire must be divided into a certain number of segments. During the simulation process, AN-SOF needs to determine the unknown current on each segment. When you access the Attributes page, a default Number of Segments is displayed. This default number is calculated based on the wire’s length and the shortest wavelength, but you can modify it as needed.
Note
If you set the Number of Segments to zero, AN-SOF will automatically compute the minimum recommended number of segments for the wire. This calculation assumes 10 segments per wavelength, considering the shortest wavelength in a frequency sweep.
Cross-Section
The Cross-Section of the wire can be chosen from a combo-box. There are six cross-section types available: Circular, Square, Flat, Elliptical, Rectangular, and Triangular. AN-SOF computes an equivalent radius for the five last cases. Infinitesimally thin wires are not allowed, so the cross-section radius must be greater than zero.
The Draw dialog box for any wire type has its own Attributes page with the same features as those described here.
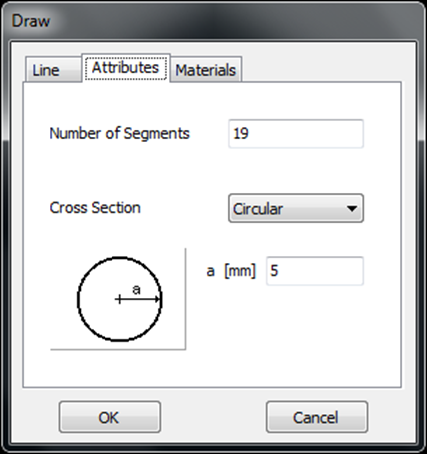
The Materials page belongs to the Draw dialog box of the chosen wire type, Fig. 1.
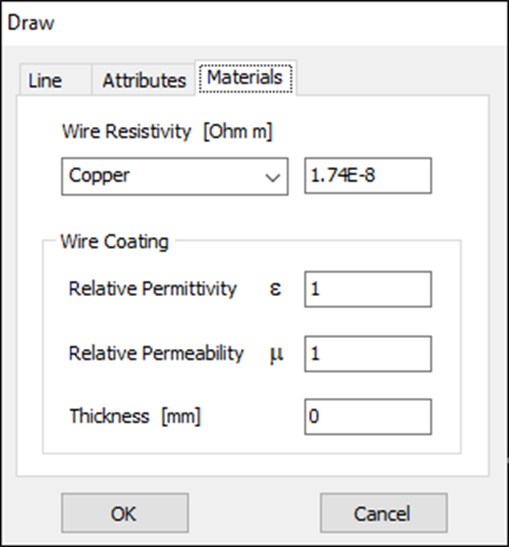
In the Materials page the following attributes can be specified:
Wire Resistivity
A resistivity in [Ohm meter] can be specified for the wire. The following list of most common metals is available for choosing:
| Material (Metals) | Resistivity [Ω m] |
| Aluminum (Pure) | 2.65E-8 |
| Aluminum (6061-T6) | 4.01E-8 |
| Aluminum (6063-T832) | 3.25E-8 |
| Brass | 6.41E-8 |
| Carbon Steel | 1.67E-7 |
| Constantan | 4.42E-7 |
| Copper | 1.74E-8 |
| German Silver | 3.33E-7 |
| Germanium | 4.55E-7 |
| Gold | 2.44E-8 |
| Iron | 9.71E-8 |
| Manganin | 4.41E-7 |
| Nichrome | 1.00E-6 |
| Nickel | 6.90E-8 |
| Phosphor Bronze | 1.10E-7 |
| Silver | 1.59E-8 |
| Solder | 1.43E-7 |
| Stainless Steel | 9.09E-7 |
| Stainless Steel 302 | 7.19E-7 |
| Tin | 1.14E-7 |
| Tungsten | 5.49E-8 |
| Zinc | 5.90E-8 |
The corresponding resistivity value will be automatically displayed for the chosen metal. Choose the Custom option to set a resistivity value if it is not in the list. Choose Perfect (PEC) to set a perfect electrically conducting metal.
The resistivity is used for computing a distributed impedance per unit length along the wire, which considers the skin effect. The equivalent radius for wires of non-circular cross section will be used to compute the impedance per unit length along the wires.
The resistivity of wires is considered in the simulation if the option Wire Resistivity is checked in the Settings panel of the Setup tabsheet.
Wire Coating
Wires can have insulation or coating material. The cross section of a coated wire is circular, so the equivalent radius will be used for wires having a non-circular cross section. In this case, the material the coating is made of can be set by the following parameters:
- Relative Permittivity: It is the dielectric constant of the coating material relative to the permittivity of vacuum.
- Relative Permeability: It is the magnetic permeability of the coating material relative to the permeability of vacuum.
- Thickness: It is the thickness of the coating shield. It can be set to zero when no coating is used.
The wire coating is considered in the simulation if the option Wire Coating is checked in the Settings panel of the Setup tabsheet.
If wires with non-zero resistivity have been drawn previously and the whole structure must now be considered as a perfect electric conductor, all resistivities can be disabled without modifying the definitions of the wires.
Go to the Setup tabsheet in the main window and select the Settings panel, Fig. 1. If the option Wire Resistivity in this panel is checked, the resistivities are enabled. Uncheck the Wire Resistivity option to disable all of them.
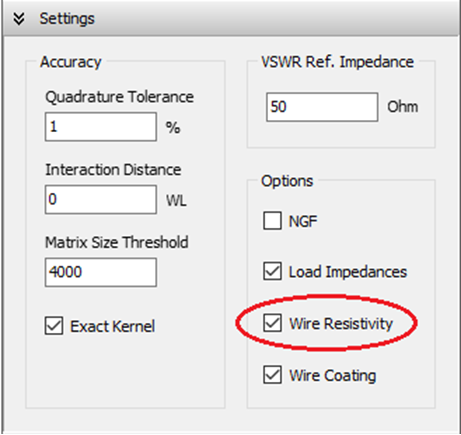
If wires with a coating shield or insulation have been drawn previously and the whole structure must now be considered as composed of bare conductive wires, all coatings can be disabled without modifying the definitions of the wires.
Go to the Setup tabsheet in the main window and select the Settings panel, Fig. 1. If the option Wire Coating in this panel is checked, the coatings are enabled. Uncheck the Wire Coating option to disable all of them.
The wire cross-section can be chosen from a combo-box in the Attributes page of the Draw dialog box for the chosen wire type, Fig. 1.
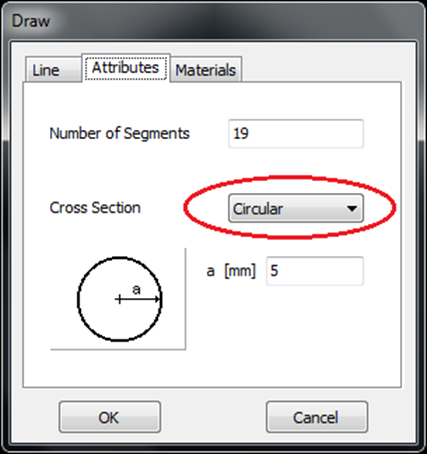
There are six cross-section types available: Circular, Square, Flat, Elliptical, Rectangular, and Triangular. AN-SOF computes an equivalent radius for the non-circular cross-sections. The equivalent radius is the radius of a circular cross-section that produces the same average electromagnetic fields around the wire and on its surface.
The cross-sections and their equivalent radii are the following:
Circular
A positive and non-zero radius “a” must be set. The equivalent radius is “a”.
Square
A positive and non-zero width “w” must be set. The equivalent radius is 0.59017 w.
Flat
A positive and non-zero width “w” must be set. The equivalent radius is w/4.
Elliptical
The semi-axes “a” and “b” must be positive and non-zero. The equivalent radius is (a + b)/2.
Rectangular
The widths “w” and “t” must be positive and non-zero. The equivalent radius is computed using a polynomial and logarithmic approximation to the solution of an integral equation.
Triangular
A positive and non-zero width “w” must be set. The equivalent radius is 0.42 w.
You can export linear wires from AN-SOF to a text file in NEC format (extension .nec) by navigating to File > Export Wires in the main menu. Linear wires will be saved as GW lines. Additionally, the exported file will include GE (ground connections), GN (ground plane), TL (transmission line), LD (load impedances and wire conductivity), IS (wire insulation), FR (frequency), EX (excitation), EK (exact kernel), and RP (radiation pattern) cards.
Moreover, the exported file can be saved as a Scilab script, with a .sce extension. The exported file will contain programming code that can be adjusted to create a new project, allowing for variations in parameters such as wire lengths and positions, frequencies, and ground conditions.
Adding Wires
A Line represents a linear (straight) wire in AN-SOF.
Accessing the Line Dialog Box
To open the Line dialog box:
- Navigate to Draw > Line in the main menu.
- The dialog box contains three tabs: Line, Attributes, and Materials (see Fig. 1).
Line Tab: Setting Geometrical Parameters
Two options are available for defining the line:
- 2 Points
- Define the line by specifying two points:
- From Point: Starting coordinates (X1, Y1, Z1).
- To Point: Ending coordinates (X2, Y2, Z2) (see Figs. 1 and 2).
- Define the line by specifying two points:
- Start – Direction – Length
- Define the line by:
- Start Point: Initial coordinates.
- Direction: Spherical angles (Theta, Phi).
- Wire Length: Total length of the line (see Figs. 3 and 4).
- Define the line by:
Attributes Tab
- Specify the Number of Segments and Cross-Section properties (refer to Wire Attributes).
Materials Tab
- Set the Resistivity and Coating properties of the wire (refer to Wire Materials).
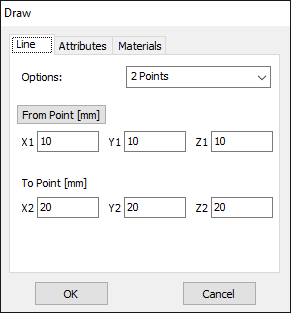
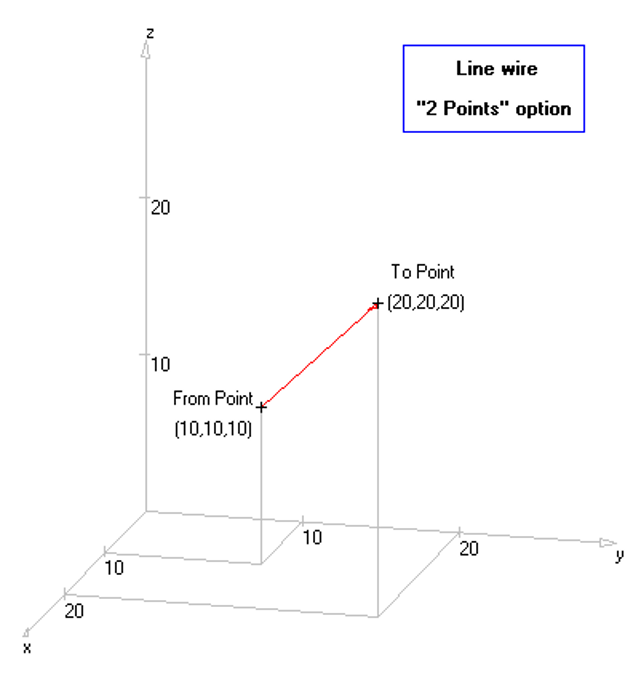
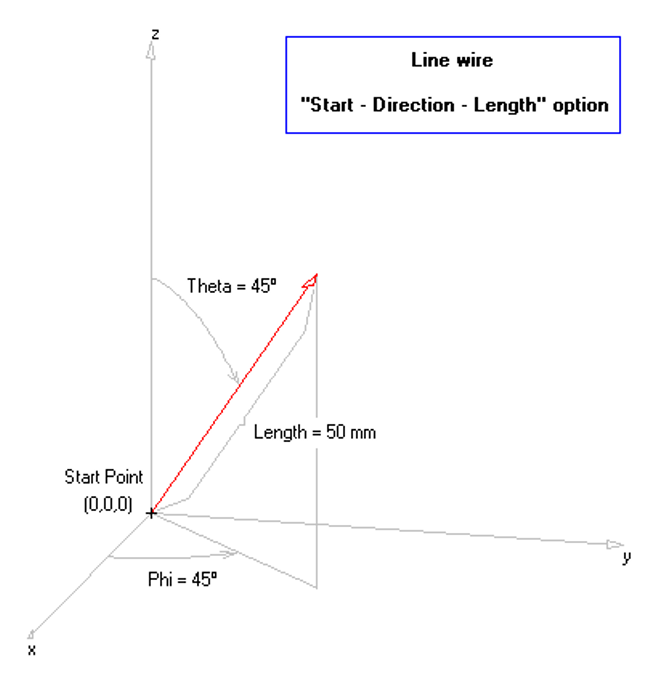
The “Arc” refers to a circular arc.
To access the “Arc” dialog box for drawing an arc, navigate to Draw > Arc in the main menu. This dialog box contains three pages: Arc, Attributes, and Materials (Fig. 1).
Arc Page
The Arc page allows you to set the geometrical parameters for the arc. Two options are available: 3 Points and Start – Center – End.
The 3 Points option enables you to define the arc by specifying three points: a Start Point, a Second Point, and an End Point. An arc starting from the Start Point, passing through the Second Point, and ending at the End Point will be drawn on the workspace (Figs. 1 and 2).
If Start – Center – End is selected, the arc will be drawn starting from the Start Point, with the center specified by Center and ending at a point determined by the End Point (Figs. 3 and 4). The End Point determines the arc’s aperture angle and the plane in which it lies. Note that the End Point may not coincide with the actual ending point of the arc.
After setting the geometrical parameters on the Arc page, you can select the Attributes page to specify the Number of Segments and Cross-Section. The Materials page allows you to set the wire Resistivity and Coating.
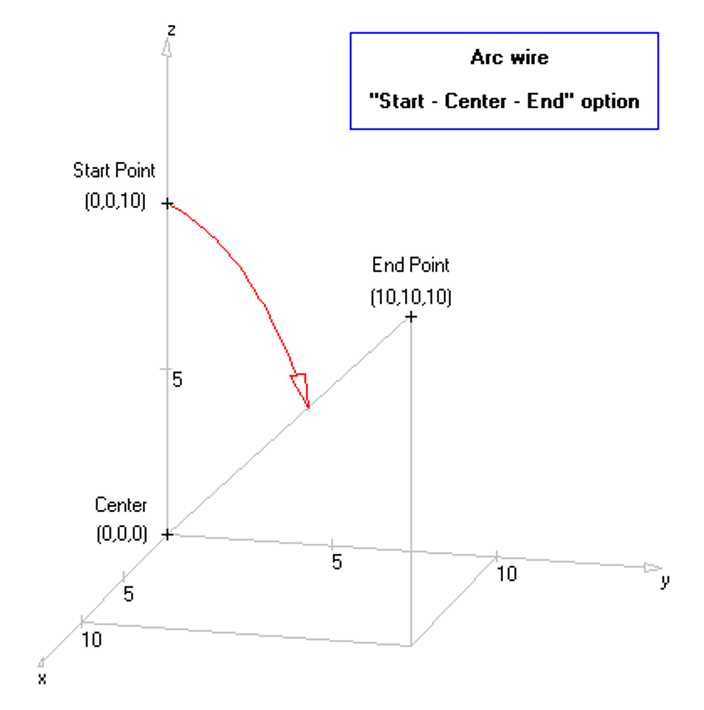
The Circle refers to a circular loop.
Go to Draw > Circle in the main menu to display the Draw dialog box for the Circle. This dialog box has four pages: Circle, Orientation, Attributes and Materials.
The Circle page
In the Circle page the geometrical parameters for the Circle can be set. There are two options: Center – Radius – Orientation and 3 Points.
The Center – Radius – Orientation option allows us entering the Circle by giving its Center, Radius, and axis, Figs. 1 and 2. The circle axis can be set in the Orientation page, Fig. 3.
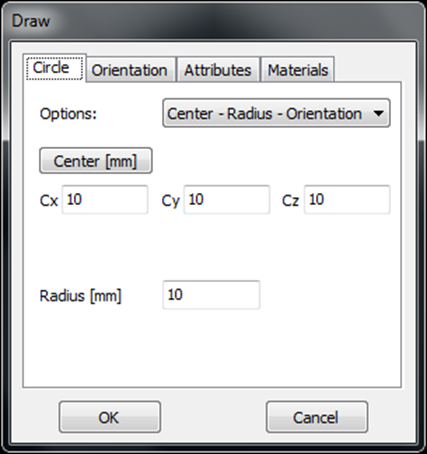
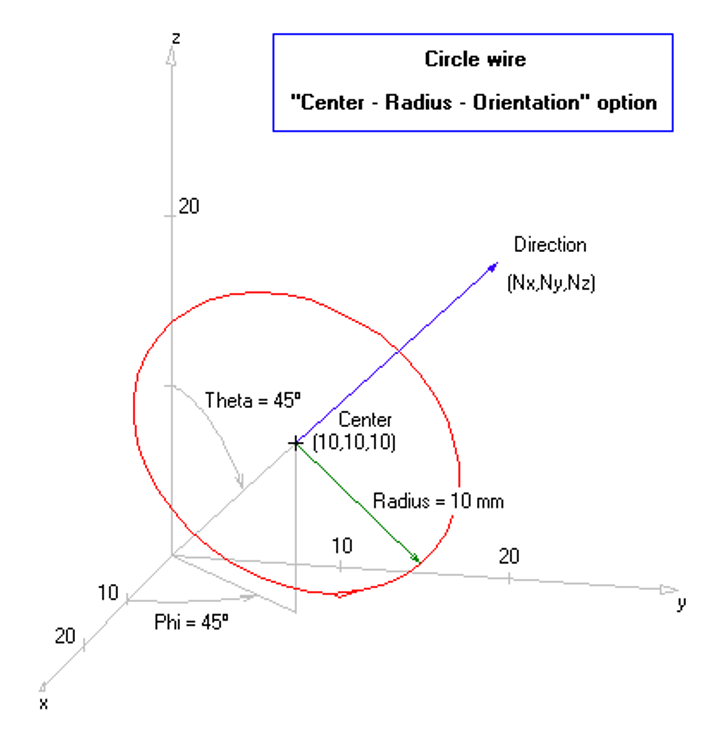
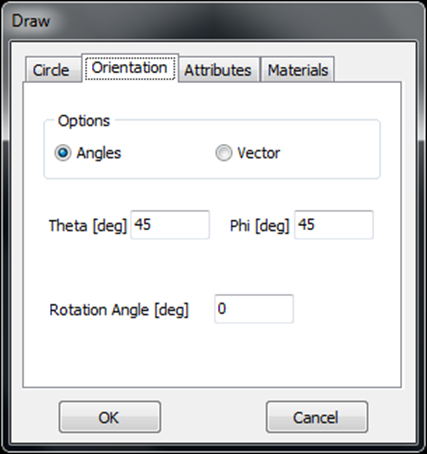
If the 3 Points option is chosen, the Circle will be drawn starting from First Point, passing through Second Point and Third Point, and ending at First Point, Figs. 4 and 5. Thus, the circle starts and ends at the same point. The Orientation page will be invisible when the 3 Points option is chosen.
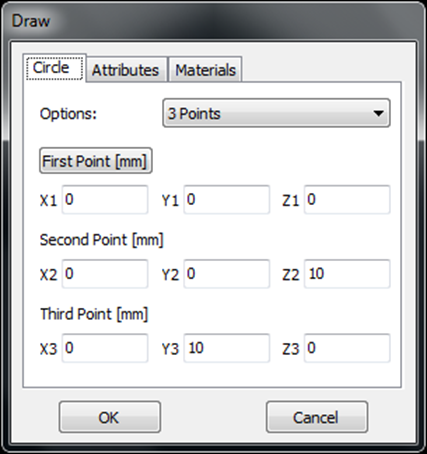
Once the geometrical parameters in the Circle and Orientation pages have been set, the Attributes > page can be selected, where the number of segments and cross-section can be set. The wire resistivity and coating can be set in the Materials > page.
The Orientation page
In the Orientation page the orientation for the Circle can be set. There is a box with two options: Angles and Vector, Fig. 3.
If Angles is selected, the circle axis can be defined by given an orthogonal direction to the rest plane of the circle. Thus, the Theta and Phi angles determine the axis direction in spherical coordinates.
If Vector is selected, the circle axis can be defined by given an orthogonal vector to the rest plane of the circle. Thus, the Nx, Ny, and Nz components of that vector determine the axis direction.
The circle can be rotated around its axis by given the Rotation Angle.
The “Helix” refers to a wire curved into a circular helical shape.
To access the “Helix” dialog box for drawing a helix, navigate to Draw > Helix in the AN-SOF main menu. This dialog box contains four tabs: Helix, Orientation, Attributes, and Materials.
Helix Page
The Helix page allows you to set the geometrical parameters for the helix. Two options are available: Start – Radius – Pitch – Turns and Start – End – Radius – Turns.
The Start – Radius – Pitch – Turns option enables you to define the helix by specifying its Start Point, Radius, Pitch, and Number of turns, as shown in Figures 1 and 2. The Pitch represents the spacing between turns. A positive (negative) pitch results in a right-handed (left-handed) helix. The Number of turns does not need to be an integer, allowing you to enter fractions of turns. Alternatively, you can enter the Diameter, Pitch Angle, and Wire Length instead of the radius-pitch-number of turns combination. When entering the Radius – Pitch – Turns combination, the Diameter – Pitch Angle – Wire Length set will be automatically calculated, and vice versa. In any case, the helix’s axial height is displayed automatically (calculated from the input data and cannot be entered).
The orientation of the helix axis can be set on the Orientation page (Fig. 3), as described below.
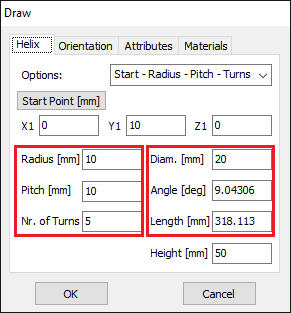
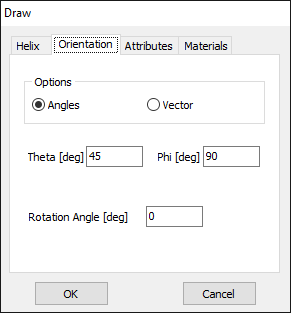
If Start – End – Radius – Turns is selected, the helix will be drawn starting from the Start Point and ending at the End Point, with the specified Radius and Number of turns, as illustrated in Figures 4 and 5. The Number of turns must be an integer, and a positive (negative) value results in a right-handed (left-handed) helix. The orientation of the helix axis is determined by the starting and ending points. The helix can be rotated around its axis by specifying a Rotation Angle. The Orientation page will be hidden when the Start – End – Radius – Turns option is chosen, as the helix axis orientation is already defined by the line connecting its start and end points.
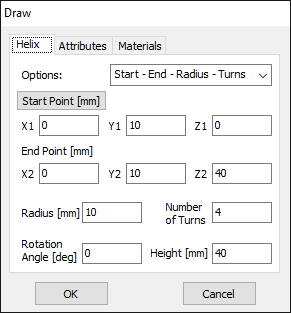
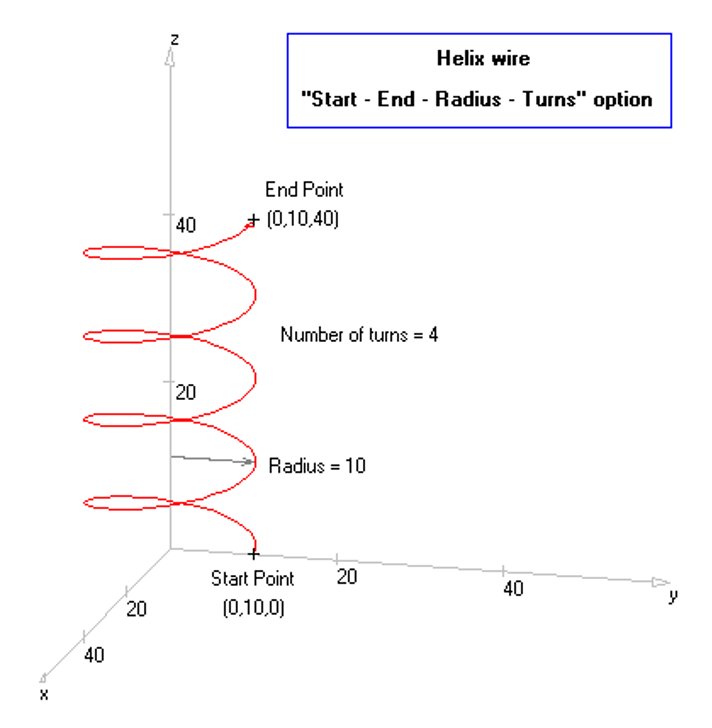
After setting the geometrical parameters on the Helix and Orientation pages, you can select the Attributes page to specify the Number of Segments and Cross-Section. The Materials page allows you to set the wire Resistivity and Coating.
Orientation Page
The Orientation page provides options for setting the helix orientation. A box with two options is available: Angles and Vector (Fig. 3).
If Angles is selected, the helix axis can be defined by specifying its direction in 3D space using the Theta and Phi angles in spherical coordinates.
If Vector is selected, the helix axis can be defined by entering a vector in the axis direction. The Nx, Ny, and Nz components determine this vector.
The helix can be rotated around its axis by specifying a Rotation Angle.
The Quadratic refers to a quadratic wire or parabola.
Go to Draw > Quadratic in the main menu to display the Draw dialog box for the Quadratic. This dialog box has three pages: Quadratic, Attributes, and Materials.
The Quadratic page
In the Quadratic page the geometrical parameters for the Quadratic can be set, Fig. 1.
The Quadratic is entered by giving three points. A quadratic curve starting from Start Point, passing through Second Point and ending at End Point will be drawn on the workspace, as shown in Figs. 2.
Once the geometrical parameters in the Quadratic page have been set, the Attributes > page can be selected, where the number of segments and cross-section can be set. The wire resistivity and coating can be set in the Materials > page.
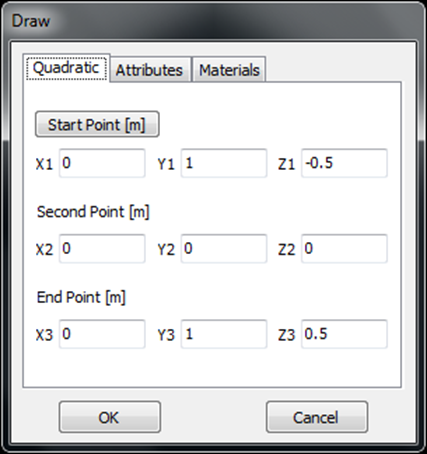
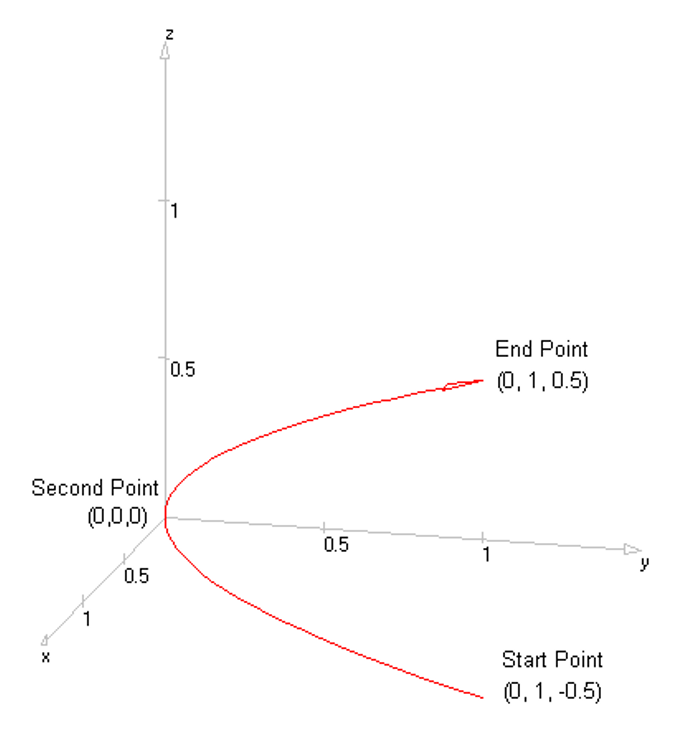
The Archimedean Spiral refers to the Archimedes’ spiral with polar equation r(α) = r0 + p/(2π) α, where r0 is the starting radius and p is the pitch. For a spiral with an integer number of turns, M, we have α = 2πM at its end point, so rend = r0 + pM, the pitch p being the separation between turns. Besides, we have that the pitch equals the constant growth rate of the spiral radius r(α) per turn, that is p = 2πdr/dα.
Go to Draw > Archimedean Spiral in the main menu to display the Draw dialog box for the Archimedean Spiral. This dialog box has three pages: Archimedean Spiral, Attributes, and Materials.
The Archimedean Spiral page
In the Archimedean Spiral page, the geometrical parameters for the Archimedean Spiral can be set, Fig. 1.
The Archimedean spiral is entered by giving the Start Point, Start Radius r0, Pitch p (positive or negative) and Number of Turns M (complete turns and fractions of a turn can be set). The spiral lies on a plane given by the Orientation Angles Theta and Phi (normal to the plane in spherical coordinates) and can be rotated by setting a Rotation Angle, Fig. 2.
Once the geometrical parameters in the Archimedean Spiral page have been set, the Attributes > page can be selected, where the number of segments and cross-section can be set. The wire resistivity and coating can be set in the Materials > page.
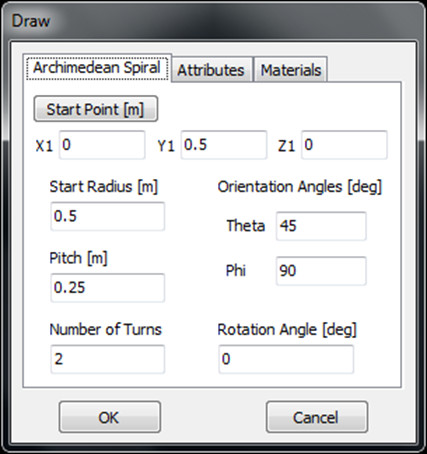
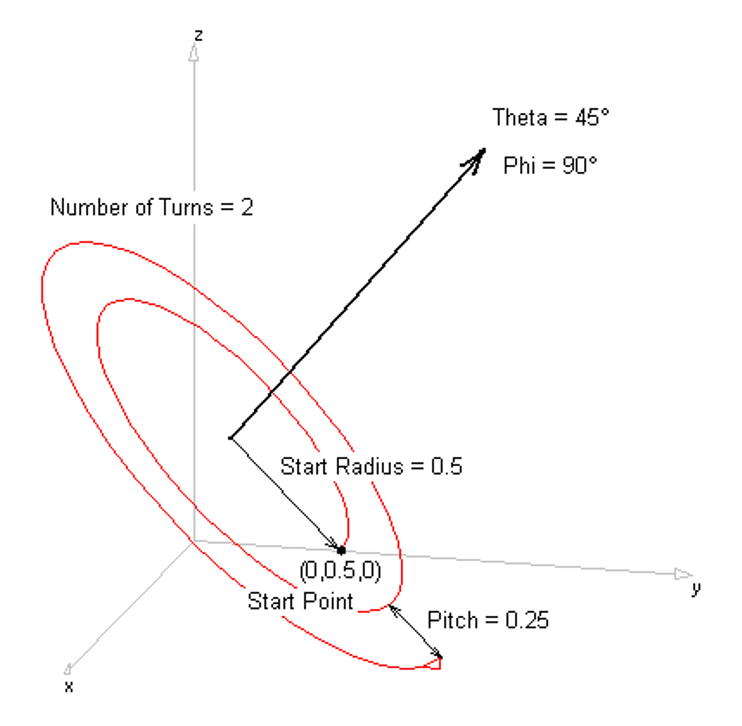
The Logarithmic Spiral refers to a spiral with polar equation r(α) = r0 exp(bα), where r0 is the starting radius (r at α = 0), b = p/(2πr0) and p is the starting pitch, that is, the derivative 2πdr/dα at α = 0 (starting growth rate of the spiral radius r(α) per turn). The first two terms of the Taylor expansion r(α) = r0 + p/(2π) α + r0(bα)2/2 + … give the polar equation of an Archimedean spiral.
Go to Draw > Logarithmic Spiral in the main menu to display the Draw dialog box for the Logarithmic Spiral. This dialog box has three pages: Logarithmic Spiral, Attributes, and Materials.
The Logarithmic Spiral page
In the Logarithmic Spiral page, the geometrical parameters for the Logarithmic Spiral can be set, Fig. 1.
The logarithmic spiral is entered by giving the Start Point, Start Radius r0, Start Pitch p (positive or negative) and Number of Turns (complete turns and fractions of a turn can be defined). The spiral lies on a plane given by the Orientation Angles Theta and Phi (normal to the plane in spherical coordinates) and can be rotated by setting a Rotation Angle, Fig. 2.
Once the geometrical parameters in the Logarithmic Spiral page have been set, the Attributes > page can be selected, where the number of segments and cross-section can be set. The wire resistivity and coating can be set in the Materials > page.

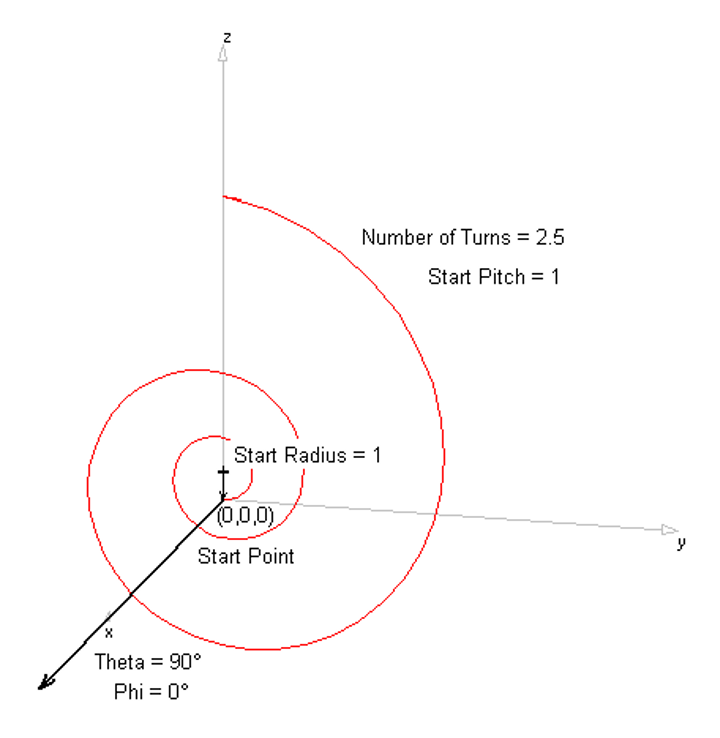
A tapered wire is a wire whose radius varies along its length. Because the change in radius occurs in discrete increments, it is also known as a stepped-radius wire. Tapered wires always have a circular cross section, and the radius typically changes linearly in defined steps—resulting in a wire with sections of constant radius, as illustrated in Fig. 1.
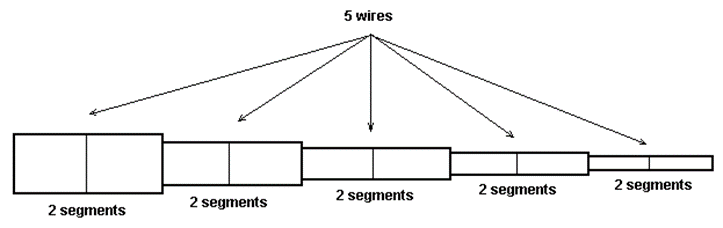
To draw a tapered wire, go to Draw > Tapered Wire in the main menu and select a wire type. The available types (e.g., Line, Arc, Circle) are the same as those found under the Draw menu. For example, Fig. 2 shows the Line page of the Draw dialog box when a linear wire type is selected.
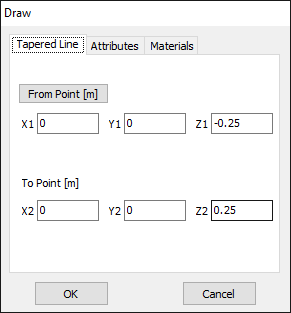
The wire must be divided into wire portions based on the desired number of radius steps, as indicated in Fig. 1. Each wire portion with a constant radius should then be subdivided into segments as required by the Method of Moments used in the simulation.
You can define the number of wire portions and the number of segments per portion in the Attributes tab (see Fig. 3). Here, you can also specify the start and end radii of the taper. To set the material properties—including the resistivity of the wire and any coating—use the Materials tab (see Fig. 4). A tapered coating can be specified by assigning start and end thickness values.
In the workspace, wire portions are shown in alternating colors for easier identification.
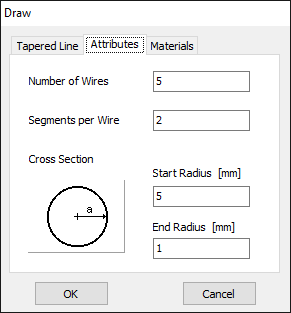
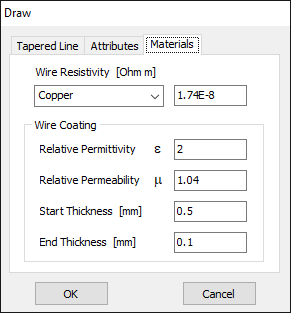
Supported Formats
To import wires from an external file into AN-SOF, follow these steps:
- Navigate to File > Import Wires in the main menu.
- A sub-menu with three options will be displayed: AN-SOF, NEC, and MM formats.
- Note that DXF and MM formats should contain only linear wires in ASCII text format.
AN-SOF Format
Wires can be imported into the AN-SOF workspace from another AN-SOF project. When a project is saved, a corresponding file with a .wre extension is created in the same directory. This file, named after the project, contains the geometrical description of all wires within the project. For details on files generated during project saves, refer to File Formats.
To import wires into your project, navigate to the main menu and select File > Import Wires > AN-SOF Format. Then, choose the specific .wre file you wish to import. You can import multiple .wre files, one at a time, as needed.
NEC Format
There are slight differences between the commands supported by AN-SOF and the standard NEC cards. To maintain compatibility with the NEC format, originally designed for data entry using punch cards, some fields appear repeating, and others must be entered with a zero, having no meaning. Lengths and wire radii are assumed to be in meters. If errors are found while importing a file, an error report will be shown in the Note panel of the Setup tab.
The SY command for symbolic variables is not supported. To run simulations with variable geometric parameters, you can write a script to sweep those parameters and generate the corresponding NEC files, then use the Run Bulk Simulation feature (see Running a Bulk Simulation).
For optimization tasks, you’ll need an optimizer script and should work with the AN-SOF Engine. Examples of parameter sweeps and optimization scripts are available in the Scripts & Optimizers category.
GW – Linear Wire
One linear wire per line must be set, beginning with “GW” and ending with an Enter, as follows:
GW Tag Segments X1 Y1 Z1 X2 Y2 Z2 Radius
[Enter]
Tag: Tag number for the linear wire (Tag > 0). The space between “GW” and Tag is optional. A single tab or comma can also be used as a separator between the command name and the first data field.
Segments: Number of segments for the wire. If zero is entered, the minimum recommended number of segments will be computed.
X1 Y1 Z1: Cartesian coordinates of the start point of the linear wire.
X2 Y2 Z2: Cartesian coordinates of the end point of the linear wire.
Radius: Wire radius.
Fields can be separated by up to two spaces, a single tab, a single comma, or a comma and space. Each GW line, including the last one in a set of linear wires to be imported, must end with an Enter (press Enter on the keyboard for a carriage return). The text lines above the GW lines will be ignored, so comments can be added at the beginning of the file.
The following are equivalent examples:
Write comments here
GW 1 12 5.42 0.38 1.262 5.425 -0.378 1.261 0.01[Enter]
GW 2 5 7.45 0 1.122 7.45 0 1.49 0.015[Enter]
GW 3 2 8.3 0.0 1.12 8.37 0.0 1.595 0.01[Enter]
Write comments here
GW1,12,5.42,0.38,1.262,5.425,-0.378,1.261,0.01[Enter]
GW2,5,7.45,0,1.122,7.45,0,1.49,0.015[Enter]
GW3,2,8.3,0.0,1.12,8.37,0.0,1.595,0.01[Enter]
CM and Other Commands
The following commands: CM (comment lines), GH (helical wire), GA (arc), GM (coordinate transformation), GS (scale dimensions), GE (ground connections), GN (real ground parameters), TL (transmission line), LD (load impedances and wire conductivity), IS (insulated wire), FR (frequency), EX (excitation), EK (exact kernel), and RP (radiation pattern), will also be read.
CM lines will be added to the Note panel of the Setup tabsheet after the NEC file is imported. The comment termination card, “CE”, is not needed in AN-SOF. Comments without the CM command at the beginning of the file will be ignored and not imported. The command names—“CM”, “GW”, “GH”, etc.—are reserved words in AN-SOF and are used to recognize the fields between these commands and the final Enter in each text line, so the command names should not be used in comments.
IMPORTANT: CM lines must always be placed at the beginning of a .nec file and kept separate from other commands.
The rest of the AN-SOF commands in NEC format are listed below, where all the indicated fields are mandatory.
GH – Helix
The GH command is used to define a helix in AN-SOF with the following syntax:
GH Tag Segments Spacing Length R R R R Radius
[Enter]
Tag: A positive number representing the tag for the helix. The space between “GH” and the Tag is optional. Note that the helix begins at the origin and develops along the positive z-axis. To adjust the helix’s position or rotation, use the GM command described below. It’s important to mention that the GH command differs in NEC-4.
Segments: The number of segments for the helix. If zero is entered, AN-SOF will compute the minimum recommended number of segments. Unlike NEC, AN-SOF uses conformal segments that precisely follow the helix contour.
Spacing: Spacing between turns.
Length: Total length of the helix. A positive Length value results in a right-handed helix, while a negative Length value produces a left-handed helix.
R: Radius of the helix (repeated four times).
Radius: Wire radius.
Note: AN-SOF uses conformal segments that exactly follow the helix contour, distinguishing it from NEC.
GA – Arc
The GA command is utilized to define an arc in AN-SOF with the following syntax:
GA Tag Segments R Ang1 Ang2 Radius
[Enter]
Tag: A positive number serving as the tag for the arc. The space between “GA” and the Tag is optional. The arc is situated on the xz-plane, centered at the origin, making the y-axis the axis of the arc. To manipulate the position or rotation of the arc, use the GM command described below.
Segments: The number of segments for the arc. If zero is entered, AN-SOF will compute the minimum recommended number of segments. It’s worth noting that, unlike NEC, AN-SOF uses conformal segments that precisely follow the arc contour.
R: Arc radius.
Ang1: The angle of the first end of the arc measured from the x-axis in a left-handed direction about the y-axis, given in degrees.
Ang2: The angle of the second end of the arc, measured in degrees.
Radius: Wire radius.
Note: AN-SOF uses conformal segments that exactly follow the arc contour, distinguishing it from NEC.
GB – AN-SOF’s Arc
The GB command is utilized to define an arc in AN-SOF with the following syntax:
GB Tag Segments Type X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3 Radius
[Enter]
Tag: A positive number serving as the tag for the arc. The space between “GB” and the Tag is optional.
Segments: The number of segments for the arc. If zero is entered, AN-SOF will compute the minimum recommended number of segments. It’s worth noting that, unlike NEC, AN-SOF uses conformal segments that precisely follow the arc contour.
Type: Type of arc. Set Type = 0 for entering three points, and Type = 1 for entering the start point, center, and end point.
X1 Y1 Z1: Cartesian coordinates of the start point of the arc.
X2 Y2 Z2: Cartesian coordinates of the second point of the arc if Type = 0, or the arc center if Type = 1.
X3 Y3 Z3: Cartesian coordinates of the end point of the arc.
Radius: Wire radius.
Note: AN-SOF uses conformal segments that exactly follow the arc contour, distinguishing it from NEC. The “GB” command is exclusive to AN-SOF and cannot be found in any NEC version.
GM – Coordinate Transformation
The GM command in AN-SOF facilitates coordinate transformations with the following syntax:
GM 0 N rotX rotY rotZ DX DY DZ 0
[Enter]
N: If N is set to 0, it implies that the entire structure above the GM command must undergo rotation and translation based on the specified values for (rotX, rotY, rotZ) and (DX, DY, DZ). The coordinate transformations are applied sequentially in that order. If N is set to 1, it indicates that the structure above the GM command must be copied, and the copy should be moved to a new position (DX, DY, DZ) from the origin. You can use the “GM” command below the “GW,” “GH,” and “GA” commands to rotate, move, and copy linear wires, helices, and arcs as needed.
rotX: Angle of rotation about the X-axis, specified in degrees.
rotY: Angle of rotation about the Y-axis, specified in degrees.
rotZ: Angle of rotation about the Z-axis, specified in degrees.
DX: Translation along the X-axis, moving the structure by an amount DX.
DY: Translation along the Y-axis, moving the structure by an amount DY.
DZ: Translation along the Z-axis, moving the structure by an amount DZ.
GS – Scale Structure Dimensions
The GS command in AN-SOF is used for scaling structure dimensions. The syntax is as follows:
GS 0 0 Scale
[Enter]
Scale: This represents the scaling factor. Applying this command results in the multiplication of all structure dimensions, including wire radii, by the specified scale value.
GE – Ground Connections
The GE command in AN-SOF is used for defining ground connections. The syntax is as follows:
GE Type
[Enter]
Type = 0: No ground plane is present. If a “GE” command is used without specifying a type, it will be interpreted as “GE 0”.
Type = 1: A PEC ground plane is placed at z = 0, and wires ending on the ground plane will be connected to the ground. If a real ground plane has been chosen, Type = 1 indicates that the wire connections to the ground must be considered as zero-Ohm connections.
Type = -1: The wire connections to the ground are imperfect and produce power losses when a real ground plane has been chosen.
GN – Real Ground
The GN command in AN-SOF is used for defining real ground parameters. The syntax is as follows:
GN Type Screen 0 0 Epsilon Sigma Length WireRadius
[Enter]
Type: Type of ground plane.
- Type = -1: Free space simulation; all ground parameters are ignored. “GN -1” can be used in this case.
- Type = 0: Reflection Coefficients/Asymptotic option.
- Type = 1: PEC ground plane at z = 0; other parameters are ignored. “GN 1” can be used in this case.
- Type = 2: Sommerfeld-Wait/Asymptotic option.
Screen: Number of radials in a radial wire ground screen. Set Screen = 0 if no ground screen is present.
Epsilon: Ground plane relative permittivity or dielectric constant.
Sigma: Ground plane conductivity in [S/m].
Length: Length of radial wires if a radial wire ground screen is used. Enter zero if no ground screen is used.
WireRadius: Radius of radial wires if a screen is used. Enter zero if no ground screen is used.
TL – Transmission Line
The TL command in AN-SOF is used to define a transmission line. The syntax is as follows:
TL Tag1 Seg1 Tag2 Seg2 Zc Length Y1r Y1i Y2r Y2i
[Enter]
Tag1: Wire tag number to which the first port of the transmission line connects.
Seg1: Segment number of wire Tag1 to which the first port of the transmission line connects.
Tag2: Wire tag number to which the second port of the transmission line connects.
Seg2: Segment number of wire Tag2 to which the second port of the transmission line connects.
Zc: Characteristic impedance of the transmission line in Ohms. A negative Zc can be entered to set a “crossed” transmission line with a 180° phase reversal relative to the reference directions of the segments. The characteristic impedance of the line is |Zc|.
Length: Length of the transmission line in meters. If Length = 0, the linear distance between the transmission line ports will be considered as the length for the line. To simulate a zero-length transmission line, enter 1E-10.
Y1r: Real part of the shunt admittance across end one of the transmission line [S].
Y1i: Imaginary part of the shunt admittance across end one of the transmission line [S].
Y2r: Real part of the shunt admittance across end two of the transmission line [S].
Y2i: Imaginary part of the shunt admittance across end two of the transmission line [S].
Refer to Adding Transmission Lines for a review of considerations when setting transmission lines, including advanced settings not available with the TL command.
LD – Load Impedance
The LD command in AN-SOF is used to define a load impedance. The syntax is as follows:
LD Type Wire# Seg# Seg# R L C
[Enter]
Type: Type of load. Series/parallel/trap RLC loads, fixed impedances R+jX, and wire conductivity can be set.
- Set Type = 0 for a series RLC load.
- Set Type = 1 for a parallel RLC load.
- Set Type = 4 for a fixed impedance R+jX. The reactance “X” must be entered in the position of “L” (the “C” field will be ignored). The reactance is fixed, so it does not scale with frequency.
- Set Type = 5 and Seg# = 0 to specify a wire conductivity [S/m] in the “R” field for the wire number “Wire#”. Use the command LD 5 0 0 0 R 0 0 to set a conductivity “R [S/m]” on all wires. “LD 5” command for setting wire conductivity must be below all LD 0, LD 1, LD 4, and LD 6 lines.
- Set Type = 6 for a trap RLC load (series RL + parallel C).
Wire#: Wire tag number where the load or conductivity is placed.
Seg#: Segment number where the load is placed. Note that it appears twice due to a NEC convention not used in AN-SOF, so the second Seg# will be ignored. Set Seg# = 0 if a wire conductivity is to be entered.
R: Resistance in Ohms or conductivity in S/m.
L: Inductance in Henries when Type = 0, or reactance in Ohms when Type = 4 (it does not scale with frequency). The “L” field is ignored if R is a conductivity, so a zero can be entered.
C: Capacitance in Farads; if none, enter zero. It is ignored if R is a conductivity, so enter zero.
IS – Insulated Wire
The IS command in AN-SOF is used to define an insulated wire. The syntax is as follows:
IS 0 Wire# 0 0 Epsilon 0 Radius
[Enter]
Wire#: Wire tag number where the insulation or coating will be applied.
Epsilon: Relative permittivity of the dielectric sheath.
Radius: Radius of the insulating sheath. Ensure it is greater than the wire radius.
FR – Frequencies
The FR command in AN-SOF defines the frequencies used in a simulation. Its syntax is:
FR Type Num 0 0 Freq Df
[Enter]
Type: Specifies the type of frequency sweep. For a linear sweep, set Type = 0; for a logarithmic sweep, set Type = 1.
Num: Number of frequency steps (Num ≥ 1).
Freq: Frequency in MHz, or the starting frequency for a range.
Df: If Type = 0, it represents the frequency stepping increment in MHz. If Type = 1, it is the multiplication factor for a logarithmic sweep.
To simulate at a single frequency, use: FR 0 1 0 0 Freq 0
EX – Excitation
The EX command in AN-SOF is used to define excitation sources for simulations. The syntax is as follows:
EX Type Wire# Seg# 0 Real Imag
[Enter]
Type: Type of source. Use Type = 0 or 5 (the “5” corresponds to an old source model used in NEC) for a voltage source. Set Type = 6 for a current source. Note that current sources in AN-SOF automatically have a non-zero internal impedance set in parallel with the source (1E6 Ohm).
Wire#: Wire tag number where the source is placed.
Seg#: Segment where the source is located.
Real: Real part of the source voltage or current.
Imag: Imaginary part of the source voltage or current.
EK – Exact Kernel
The EK command in AN-SOF is used to force the use of the Exact Kernel. The syntax is as follows:
EK
[Enter]
This command ensures that the Exact Kernel is utilized, even if this option is disabled. It’s important to note that AN-SOF has the Exact Kernel enabled by default.
RP – Radiation Pattern
The RP command in AN-SOF is used to set the radiation pattern parameters. The syntax is as follows:
RP 0 Ntheta Nphi 1001 Theta Phi Dtheta Dphi R
[Enter]
Ntheta: Number of values of Θ at which the field is to be computed.
Nphi: Number of values of φ at which the field is to be computed.
(Note: The value “1001” is a NEC variable and will be ignored since AN-SOF always computes the average power gain.)
Theta: Initial Θ angle in degrees.
Phi: Initial φ angle in degrees.
Dtheta: Increment for Θ in degrees.
Dphi: Increment for φ in degrees.
R: Radial distance in meters of the field point from the origin. R = 0 is taken as R = 1 m.
MM Format
One linear wire per line must be defined as follows:
X1,[TAB]Y1,[TAB]Z1,[TAB]X2,[TAB]Y2,[TAB]Z2,[TAB]Radius,[TAB]Segments
[Enter]
X1 Y1 Z1 = Cartesian coordinates of the wire start point.
X2 Y2 Z2 = Cartesian coordinates of the wire end point.
Radius = Wire radius.
Segments = Number of segments.
The last text line must end with an Enter (press Enter in the keyboard for a carriage return).
Example:
5.42, 0.38, 1.262, 5.425, -0.378, 1.261, 0.01, 12
7.45, 0, 1.122, 7.45, 0, 1.49, 0.015, 5
8.3, 0.0, 1.12, 8.37, 0.0, 1.595, 0.01, 2
[Enter]
In the MM format, a wire can be automatically segmented by specifying any number less than or equal to zero for the segment count. The coordinates of each wire’s start and end points must use the same length unit selected in the Preferences dialog box in AN-SOF. Similarly, the radius of any imported wire must also be expressed in the selected unit.
Linear wires can be entered and edited in a table using the Tabular Input window. To access this feature, navigate to Draw > Tabular Input (Ctrl + T) in the main menu. This opens the Tabular Input window (see Fig. 1), which contains four tabs:
- Wires:
- Allows you to enter and edit linear wires by specifying their end coordinates, number of segments, wire radius, and materials.
- Sources:
- Enables you to connect sources to the wires listed in the Wires tab. A source must be connected to a specific wire segment.
- Loads:
- Allows you to connect loads to the wires listed in the Wires tab. A load must be connected to a specific wire segment.
- Trans. Lines:
- Enables you to connect transmission lines between two wire segments listed in the Wires tab.
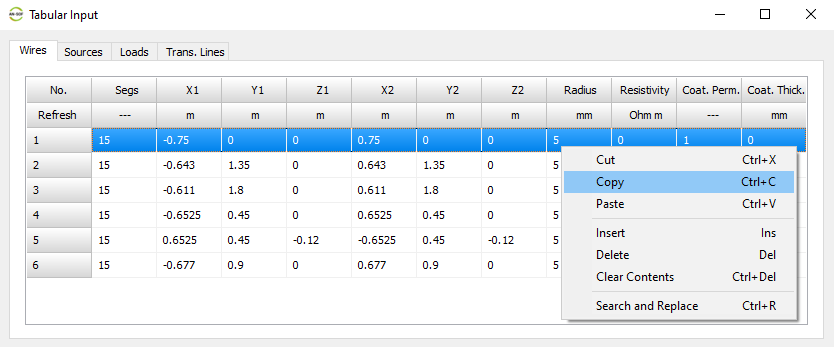
Wires Tab
Select the Wires tab and enter values as specified in the column titles (see Fig. 1). Each row corresponds to a linear wire, and you can input details such as:
- Number of segments (Segs).
- Coordinates of the starting point (X1, Y1, Z1) and ending point (X2, Y2, Z2).
- Wire radius.
- Resistivity.
- Coating (dielectric insulation).
Note: Only wires with a circular cross-section can be entered.
Table Interaction
- Right-click on the table to open a pop-up menu with standard options such as Cut (Ctrl + X), Copy (Ctrl + C), and Paste (Ctrl + V).
- Single cells can be selected by left-clicking on them or by using the TAB and arrow keys on the keyboard.
- Rows can be selected by clicking on the row number in the left column (No. column). Use the mouse or the up/down arrow keys to select a single row. The selected wire (row) is highlighted in red in the workspace. Double-click on a cell to exit row selection mode.
Row Operations
- Use Cut (Ctrl + X), Copy (Ctrl + C), and Paste (Ctrl + V) to manipulate selected rows.
- Use the Insert (Ins key) and Delete (Del key) options to add or remove rows.
- The Clear Contents (Ctrl + Del) option clears the content of a selected cell or row.
- The Search and Replace (Ctrl + R) option allows for bulk edits to wire end coordinates.
Wire Numbers in the Workspace
While the Tabular Input window is open, wire numbers are displayed in the workspace next to the corresponding wires (see Fig. 2). These numbers indicate the order of the wires in the table.
Note:
- Wires do not have permanent tags in AN-SOF. If a wire is deleted, the numbers will adjust automatically.
- Wire numbers are used solely for identification in the workspace while the Tabular Input window is open.
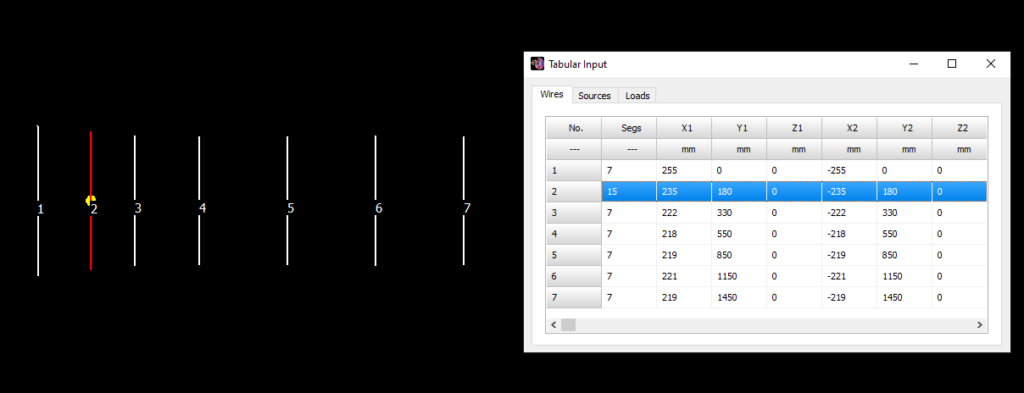
Sources Tab
Use the Sources tab to enter sources (see Fig. 3).
Entering Source Details
- Type Column: Enter “V” for a voltage source or “I” for a current source.
- Wire No. Column: Specify the wire on which the source is placed. Refer to the wire numbering in the No. column of the Wires tab.
- Position Column: Indicate the segment number where the source is connected. The segment number ranges from 1 to the number of segments (Segs) specified for the wire in the Wires tab.
- Amplitude Column: Enter the amplitude of the source in Volts or Amperes.
- Phase Column: Specify the phase of the source in degrees.
Table Interaction
- Right-click on the table to open a pop-up menu with standard options:
- Cut (Ctrl + X)
- Copy (Ctrl + C)
- Paste (Ctrl + V)
- Insert (Ins key)
- Delete (Del key)
- Clear Contents (Ctrl + Del)
These options function the same way as in the Wires tab, allowing you to manipulate cells and rows.
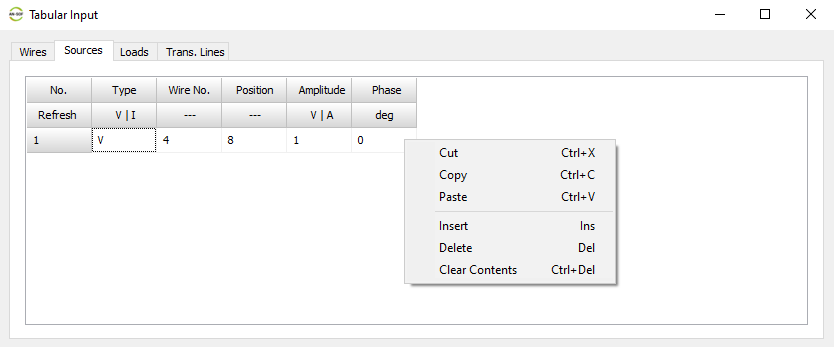
Loads Tab
Use the Loads tab to enter load impedances (see Fig. 4).
Entering Load Details
- Type Column: Enter one of the following:
- “L” for an inductor.
- “C” for a capacitor.
- “Z” for an impedance (R + jX).
- Wire No. Column: Specify the wire on which the load is placed. Refer to the wire numbering in the No. column of the Wires tab.
- Position Column: Indicate the segment number where the load is connected. The segment number ranges from 1 to the number of segments (Segs) specified for the wire in the Wires tab.
- R Column: Enter the resistance value (R) in Ohms.
- Last Column: Depending on the option entered in the Type column, input one of the following:
- Inductance (L) in the displayed unit.
- Capacitance (C) in the displayed unit.
- Reactance (X) in Ohms.
Table Interaction
- Right-click on the table to open a pop-up menu with standard options:
- Cut (Ctrl + X)
- Copy (Ctrl + C)
- Paste (Ctrl + V)
- Insert (Ins key)
- Delete (Del key)
- Clear Contents (Ctrl + Del)
These options function the same way as in the Wires tab, allowing you to manipulate cells and rows.
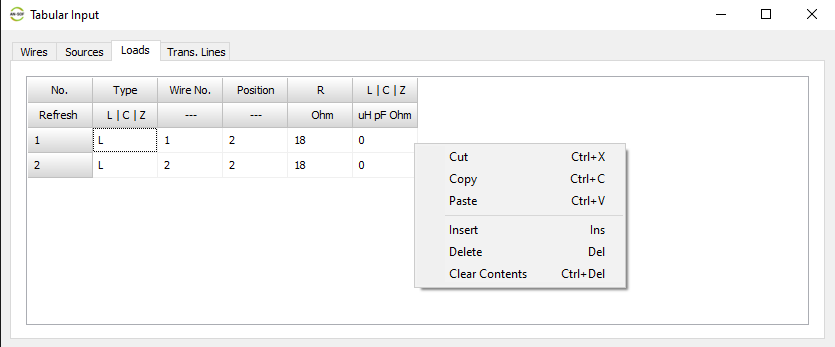
Trans. Lines Tab
Use the Trans. Lines tab to enter transmission lines and connect them to wire segments (see Fig. 5).
Entering Transmission Line Details
- Port 1 Columns:
- Specify the wire segment where Port 1 of the transmission line is connected by entering the Wire No. and Position. Refer to the numbering and number of segments specified for each wire in the Wires tab.
- Port 2 Columns:
- Similarly, specify the wire segment where Port 2 of the transmission line is connected by entering the Wire No. and Position.
- Additional Columns:
- Complete the Type, Z0 (characteristic impedance), VF (velocity factor), Length, and other columns as explained in the section Adding Transmission Lines.
- To simplify the process, select a row and double-click on an option in the right panel, which contains a collection of transmission line types with preloaded parameters.
Table Interaction
- Right-click on the table to open a pop-up menu with standard options:
- Cut (Ctrl + X)
- Copy (Ctrl + C)
- Paste (Ctrl + V)
- Insert (Ins key)
- Delete (Del key)
- Clear Contents (Ctrl + Del)
These options function the same way as in the Wires tab, allowing you to manipulate cells and rows.
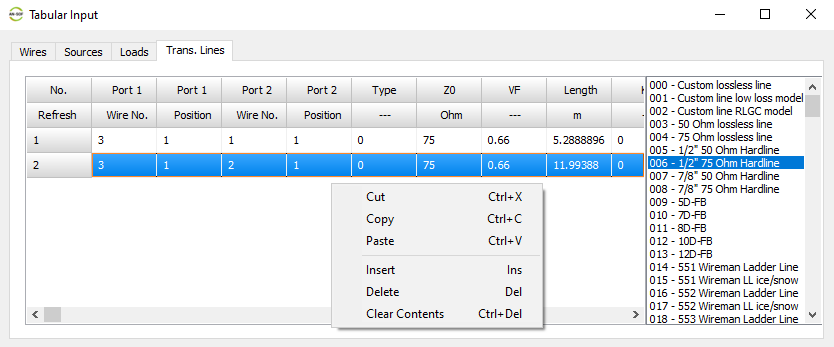
Note:
- Entering a zero in Wire No., regardless of the Position entered, disconnects the port from the wire (putting the transmission line port in FREE status).
- Only transmission lines with both ports connected to wire segments will be considered in a simulation.
- Clicking on a row number (first column of the table) in the Trans. Lines tab highlights the transmission line in red in the AN-SOF workspace.
Refresh Button
A Refresh button is located just below the No. cell in all tabs of the Tabular Input window (see Fig. 6). Click the Refresh button to instantly apply changes. This eliminates the need to close and reopen the Tabular Input window to apply modifications.
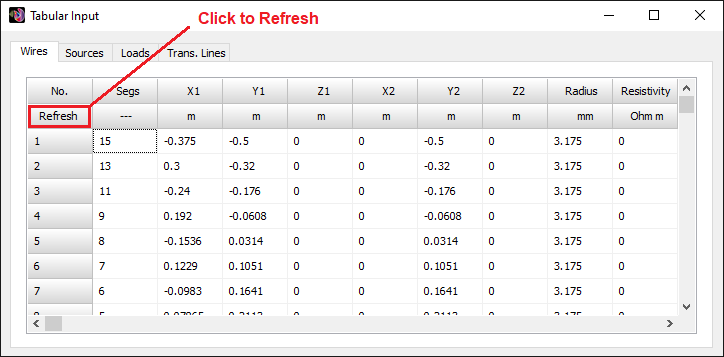
Editing Wires
Ways to Select a Wire
Selecting a wire in the workspace allows you to edit it, visualize its properties, or view simulation results. You can select any wire using one of the following methods:
- Using the Select Wire Tool: Click the Select Wire button (arrow icon) on the toolbar, and then left-click on the desired wire.
- Right-Clicking the Wire: Right-click on the wire to open a pop-up menu (see Fig. 1).
- Using Keyboard Shortcuts: Press F8 or F9 to select wires one by one, either forwards or backwards, in the order they were created.
Double-click on the workspace or press ESC to deselect the wire.
When a wire is selected, it will be highlighted in light blue for easy identification. Once selected, you can:
- Edit the wire.
- View its properties, such as geometrical details, electrical length, number of segments, wire radius, and materials.
- Visualize simulation results, such as current distribution or input impedance (if the wire has a source on one of its segments).
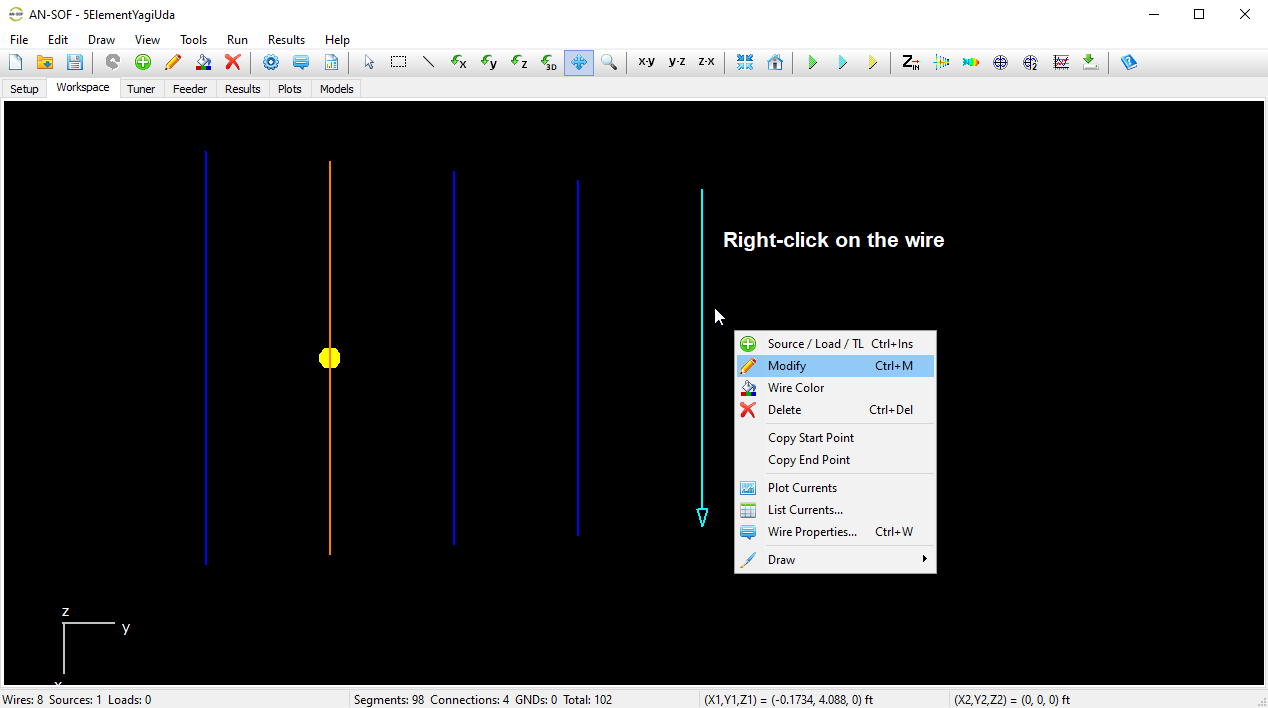
The Pop-Up Menu
Right-clicking on a wire opens a pop-up menu with the following commands:
Source / Load / TL (Ctrl + Ins)
Opens the Source / Load / TL toolbar, allowing you to connect a source, load impedance, or transmission line to a segment of the selected wire.
Modify (Ctrl + M)
Opens the Modify dialog box to edit the selected wire.
Wire Color
Opens a dialog box to change the color of the selected wire.
Delete (Ctrl + Del)
Deletes the selected wire, including all sources and loads placed on it. Transmission line connections will also be removed.
Copy Start Point
Copies the start point of the selected wire, enabling you to connect it to the end of another wire.
Copy End Point
Copies the end point of the selected wire, enabling you to connect it to the end of another wire.
Plot Currents
Opens a chart in the AN-XY Chart application, displaying the current distribution along the selected wire. This option is enabled only after currents have been computed.
List Currents
Opens the List Currents toolbar, allowing you to select a wire segment and tabulate its current versus frequency. This option is enabled only after currents have been computed.
Wire Properties (Ctrl + W)
Opens the Wire Properties dialog box, where you can view the geometry, attributes, and material data of the selected wire.
Draw
Contains a sub-menu with commands to draw various types of wires, including:
To modify an existing wire, right-click on it and choose Modify from the pop-up menu. This opens the Modify dialog box, where you can adjust the wire’s geometric parameters and attributes.
Alternatively, you can use the Select Wire button (arrow icon) from the main toolbar. After clicking this button, left-click on the wire you wish to modify. Once selected, go to Edit > Modify in the main menu. Note that this option is only enabled when a wire is selected.
Fig. 1 shows how to access the Modify command for a linear wire.
To delete a wire, right-click on it and select Delete from the pop-up menu. This will remove the selected wire from the model. Note that any sources or loads attached to the wire will also be deleted.
Alternatively, you can delete a wire using the Select Wire button (arrow icon) in the main toolbar. Click the button, then left-click on the wire to select it. Once selected, go to Edit > Delete in the main menu. This option is only enabled when a wire is selected.
Fig. 1 shows how to delete a linear wire using these options.
To enable a confirmation prompt before deleting a wire, go to Tools > Preferences > Options and check the option “Ask before deleting wires.”
AN-SOF allows you to simultaneously edit a group of wires. There are three ways to select multiple wires for editing:
- Using the Selection Box Tool: Drag a rectangular box to select multiple wires.
- Selecting Wire by Wire: Left-click on individual wires while holding the Ctrl key.
- Combination of Both Methods: Use a mix of the Selection Box tool and wire-by-wire selection.
Using the Selection Box Tool
- Click the Selection Box button on the main toolbar.
- Left-click on the workspace and drag a box to select multiple wires (see Fig. 1).
- All wires within the selection box will be highlighted in light blue.
- Dragging the box from top to bottom selects only fully enclosed wires.
- Dragging the box from bottom to top selects partially enclosed wires as well.
- Enclosing already selected wires with the selection box will deselect them.
- To deselect all wires, double-click on the screen or press ESC.
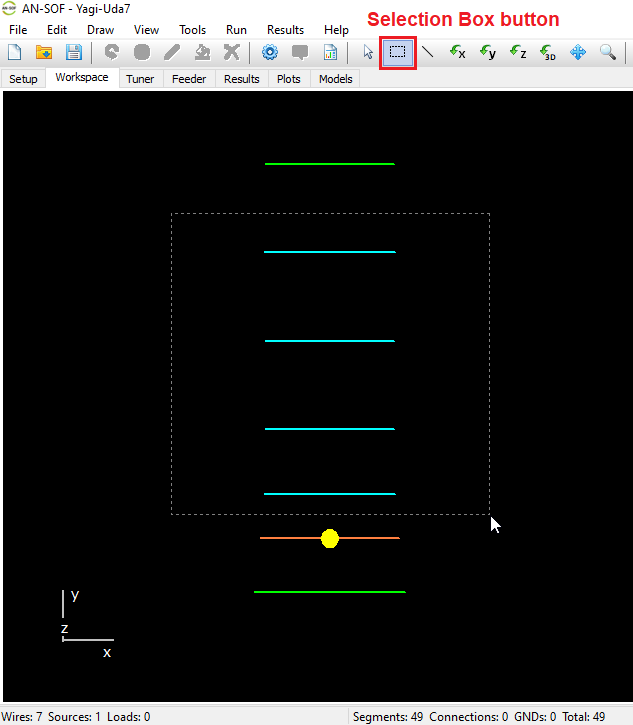
Selecting Wire by Wire
- Click the Select Wire button (arrow icon) on the main toolbar (Fig. 2).
- Hold the Ctrl key and left-click on individual wires to select them.
- To deselect a wire, hold the Ctrl key and click on it again.
- To deselect all wires, double-click on the screen or press ESC.
Wire Selection Methods – Video Tutorial
Watch the video below to learn how to efficiently select and edit wires in your antenna models. This tutorial demonstrates various selection techniques, including the ‘Select Wire’ and ‘Selection Box’ tools, using Ctrl + Left-Click for multi-selection, and combining these methods to streamline your workflow.
Persistent Wire Selections
Wire selections in AN-SOF persist until you explicitly deselect them—by double-clicking or pressing ESC—making it easier to apply consecutive modifications and run simulations between changes without the need to reselect elements. Even after saving and reopening a project, selected wires remain highlighted, allowing you to seamlessly resume editing exactly where you left off.
AN-SOF also includes Undo/Redo functionality, with up to 10 levels of action history. These options are available via the Edit menu and the main toolbar, or using the shortcuts Ctrl + Z (Undo) and Ctrl + Y (Redo). Together with persistent wire selections, this enables a smooth and efficient iterative workflow, where you can make changes, simulate, and refine your model until the desired outcome is achieved.
This process is illustrated in the video below and the accompanying flowchart (Fig. 3), with a detailed explanation provided beneath the diagram.
Step-by-Step Iterative Workflow
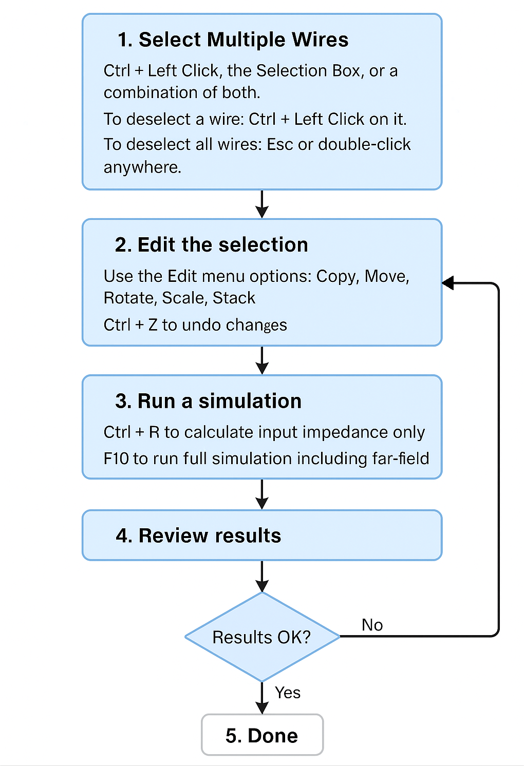
1️⃣ Select Multiple Wires
- Use Ctrl + Left Click, the Selection Box, or both.
- Selected wires are highlighted in light blue.
- To deselect a wire: Ctrl + Left Click on it.
- To deselect all wires: Press ESC or double-click anywhere on the workspace.
2️⃣ Edit the Selection
- Use the Edit menu options: Modify, Move, Rotate, Scale, Copy, Stack.
3️⃣ Run a Simulation
- Press Ctrl + R to calculate input impedance only.
- Press F10 to run the full simulation including far-field results.
4️⃣ Review Results
5️⃣ Continue Editing
- Selected wires remain highlighted after simulation.
- Resume scaling, moving, rotating, etc., without reselecting.
- Use Ctrl + Z / Ctrl + Y to undo/redo changes.
🔁 Iterate as Needed
- Edit, simulate, and fine-tune your model continuously until you achieve the desired result.
🆕 Improved View Adjustments
Modifying the Selected Wires
Once multiple wires have been selected, navigate to Edit > Modify in the main menu to modify them. The Modify command opens a dialog box (see Fig. 4) with three tabs: Attributes, Materials, and Sources/Loads. Use the checkboxes to specify which parameters you want to modify.
In the Attributes tab, the Segments per Wire and Segments per Wavelength options allow for bulk editing of wire segments. These options are mutually exclusive:
- Segments per Wire sets a fixed number of segments for all selected wires.
- Segments per Wavelength sets the number of segments for each wire based on its length in wavelengths, using the shortest wavelength corresponding to the highest frequency specified.
Entering “0” (zero) in the Segments per Wire field will automatically set the number of segments for each wire based on 10 segments per wavelength.
In the Sources/Loads tab, you can remove sources and loads in bulk by selecting “Delete Sources” or “Delete Loads”.
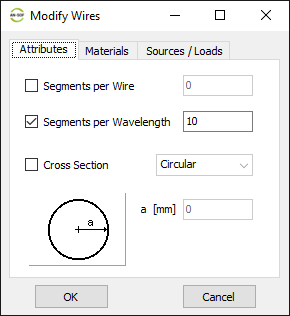
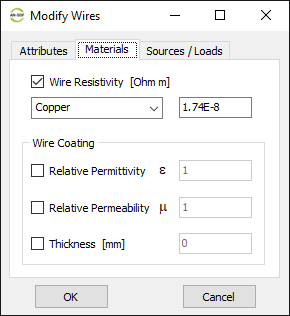
If you need to manipulate the position or arrangement of selected wires—such as moving, rotating, scaling, copying, or stacking them—rather than editing their attributes like the number of segments, cross-section, or material properties, refer to the following articles:
You can delete multiple wires at once by first selecting them using one of the following methods:
- Selection Box – Click and drag a rectangular box around the wires you want to select.
- Wire-by-Wire – Hold down the Ctrl key and left-click on each wire individually.
- Combination – Combine both methods for more flexible selection.
For step-by-step instructions on selecting multiple wires, see the article:
Once the wires are selected, you can delete them using one of the following methods:
- Go to Edit > Delete in the main menu
- Press Ctrl + Del on your keyboard
- Click the Delete button in the toolbar
Fig. 1 shows how to select three wires using the Select Wires tool (arrow icon) and Ctrl + left-click, followed by clicking the Delete button in the toolbar.
To enable a confirmation prompt before deleting wires, go to Tools > Preferences > Options and check the option “Ask before deleting wires.”
To change the color of a wire, right-click on it to bring up the pop-up menu. Select the Wire Color command to open a dialog box where you can choose a color for the wire. This command is enabled only when a wire is selected.
Alternatively, you can access the Wire Color command by:
- Clicking the Select Wire button (arrow icon) on the toolbar.
- Left-clicking on the wire to select it.
- Navigating to Edit > Wire Color in the main menu.
The Wire Color command is also available as a button on the toolbar.
To change the color of a group of wires (Fig. 1):
- Select the wires using the Selection Box or by selecting them individually (as explained in the section Selecting and Modifying Multiple Wires).
- Navigate to Edit > Wire Color in the main menu.
Right-clicking on a wire displays a pop-up menu, where you can select the Wire Properties command.
Alternatively, you can access the Wire Properties command by:
- Clicking the Select Wire button (arrow icon) on the toolbar.
- Left-clicking on the wire to select it.
- Navigating to Edit > Wire Properties in the main menu.
The Wire Properties command is also available as a button on the toolbar.
Executing the Wire Properties command opens the Wire Properties window, which contains three tabs: Geometry, Attributes, and Materials. This window is designed for viewing wire properties only. To edit a wire, refer to the section Modifying a Wire.
The Geometry Tab
This tab displays the geometrical properties of the selected wire (see Fig. 1), including:
- Start Point: Cartesian coordinates of the wire’s start point.
- End Point: Cartesian coordinates of the wire’s end point.
- Wire Length: Length of the wire.
- Segment Length: Length of a wire segment. For curved wires with non-uniform segments, this is the average segment length.
- Shortest Wavelength (λ): Wavelength corresponding to the highest frequency specified in the Frequency panel.
- Wire Length/λ: Wire length measured in wavelengths (based on the shortest wavelength).
- Segment Length/λ: Length of a wire segment in wavelengths (based on the shortest wavelength).
- Segments Per Wavelength: Number of segments the wire would have if its length were one wavelength. This is the inverse of the segment length measured in wavelengths: 1/(Segment Length/λ).
- Hallen’s Parameter (Ω): A parameter that measures wire thickness, defined as Ω = 2 ln(L/a), where L is the wire length and a is the wire radius.
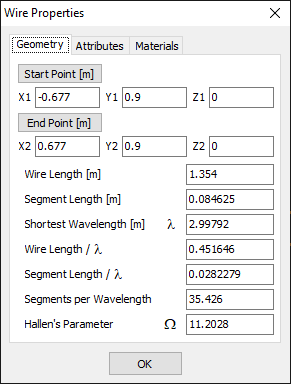
The Attributes Tab
This tab displays the electrical properties of the selected wire (see Fig. 2), including:
- Number of Segments: Number of segments into which the wire is divided.
- Number of Sources: Number of sources placed on the wire.
- Number of Loads: Number of loads placed on the wire.
- Cross-Section: Type and dimensions of the wire’s cross-section.
- Equivalent Radius: Equivalent radius of the cross-section.
- Equivalent Radius/λ: Equivalent radius as a fraction of the shortest wavelength.
- Thin-Wire Ratio: Ratio of the wire diameter to the segment length. This must be less than 3 when the Exact Kernel option is unchecked in the Settings panel of the Setup tab. If the Exact Kernel option is checked, any value of the thin-wire ratio is allowed. For non-circular cross-sections, the wire diameter is twice the equivalent radius.
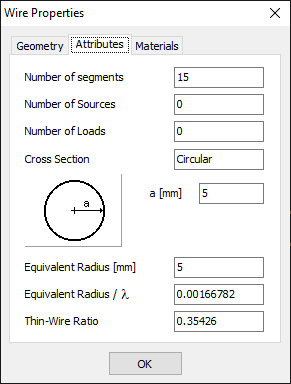
The Materials Tab
This tab displays the material properties of the selected wire (see Fig. 3), including:
- Wire Resistivity: Resistivity of the wire in [Ohm·m]. If the wire is coated, this refers to the resistivity of the internal conductor.
- Wire Coating: Parameters of the wire’s coating shield.
- Relative Permittivity: Permittivity (dielectric constant) of the coating material relative to the permittivity of vacuum.
- Relative Permeability: Magnetic permeability of the coating material relative to the permeability of vacuum.
- Thickness: Thickness of the coating shield.
A wire junction is automatically established when the coordinates of a wire end match the end coordinates of a previously added wire. Wire junctions are essential to satisfy Kirchhoff’s current law at the connection point.
Figure 1 illustrates the correct and incorrect ways to connect two wires. To connect the end of wire 1 to a point on wire 2 that is not an end, you must split wire 2 into two wires. This means three wires will be needed instead of two to make the connection.
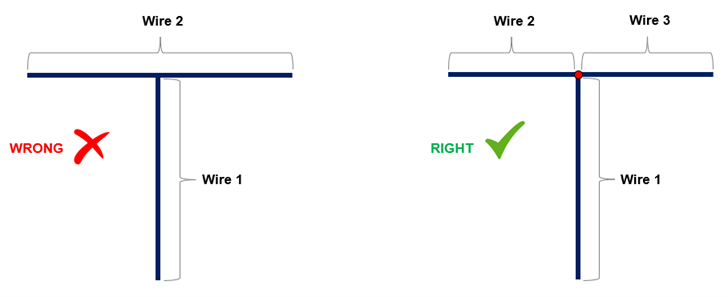
Connecting Wires by Copying and Pasting Ends
Two wires can be connected by copying and pasting their ends:
- Right-click on a wire to select it.
- From the pop-up menu, choose Copy Start Point or Copy End Point to copy the coordinates of the wire end to an internal clipboard.
- Paste the copied point in the Draw dialog box when adding a new wire by clicking the From Point button, located just above the start point coordinates (X1, Y1, Z1) (see Fig. 2).
Note:
- When a wire is selected in the workspace, it will be highlighted in light blue, and an arrow will appear at the End Point. The opposite end is the Start Point.
- Wire orientation serves as the electrical reference for the phase of the current distribution. However, it does not affect observables such as input impedance (and thus VSWR or S11) or radiation pattern metrics (directivity, gain, efficiency, etc.).
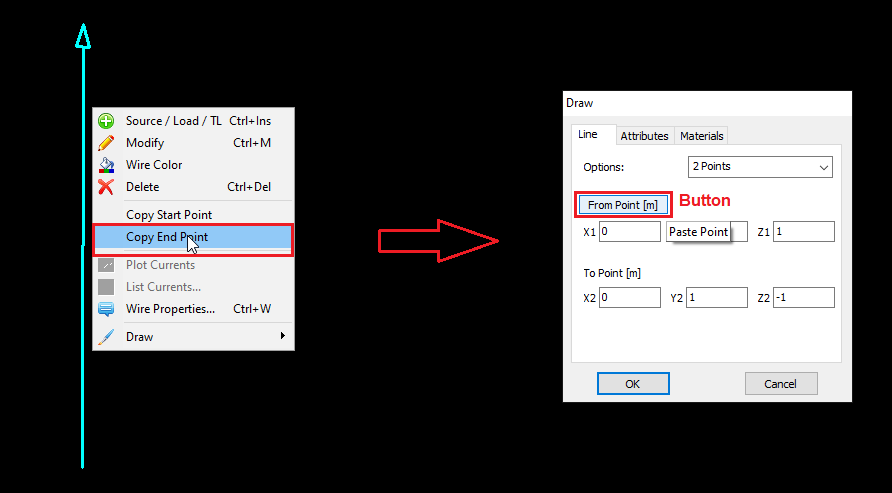
Copying Start and End Points via the Wire Properties Window
The Start and End Points of a wire can also be copied to the AN-SOF internal clipboard for use in a dialog box to draw another wire, using buttons in the Wire Properties window. This procedure is demonstrated in the video below and explained in detail in the following section.
Procedure for Connecting Two Wires at Their Ends
This procedure demonstrates how to connect the Start or End Point of wire #1 to the Start Point of wire #2:
- Right-click on wire #1 to display a pop-up menu.
- Choose the Copy Start Point or Copy End Point command. This command is also available in the Wire Properties window of the selected wire (see Fig. 3).
- In this example, wire #2 will be a Line. Navigate to Draw > Line in the main menu to open the Draw dialog box for the Line.
- Click the From Point button to paste the copied point (see Fig. 4). Then, complete the definition of wire #2.
Using this procedure, any number of wires can be connected at the same point.
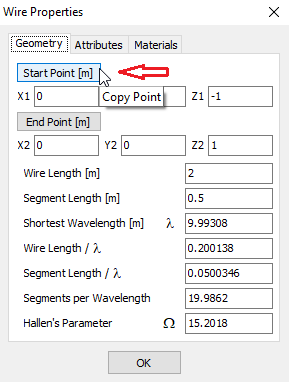
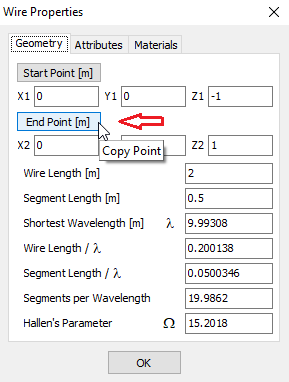
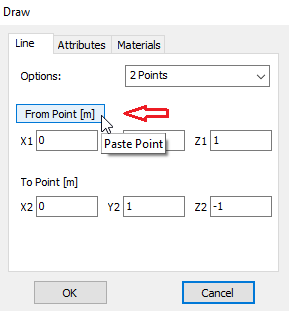
After drawing the wire structure, you may need to adjust the position, orientation, or size of individual wires or groups of wires. To modify wires, you must first select them.
Selecting Wires
- Using the Selection Box:
- Click the Selection Box button on the toolbar.
- Drag a box using the mouse while holding the left button to enclose the wires you want to modify (see Fig. 1).
- Dragging the box from top to bottom selects only fully enclosed wires.
- Dragging the box from bottom to top selects partially enclosed wires as well.
- Enclosing already selected wires with the selection box will deselect them.
- Selecting Wire by Wire:
- Click the Select Wire button (arrow icon) on the toolbar.
- Hold the Ctrl key and left-click on individual wires to select them.
- To deselect a wire, hold the Ctrl key and click on it again.
- To deselect all wires, double-click on the screen or press ESC.
You can also combine the Selection Box method with selecting wires individually.
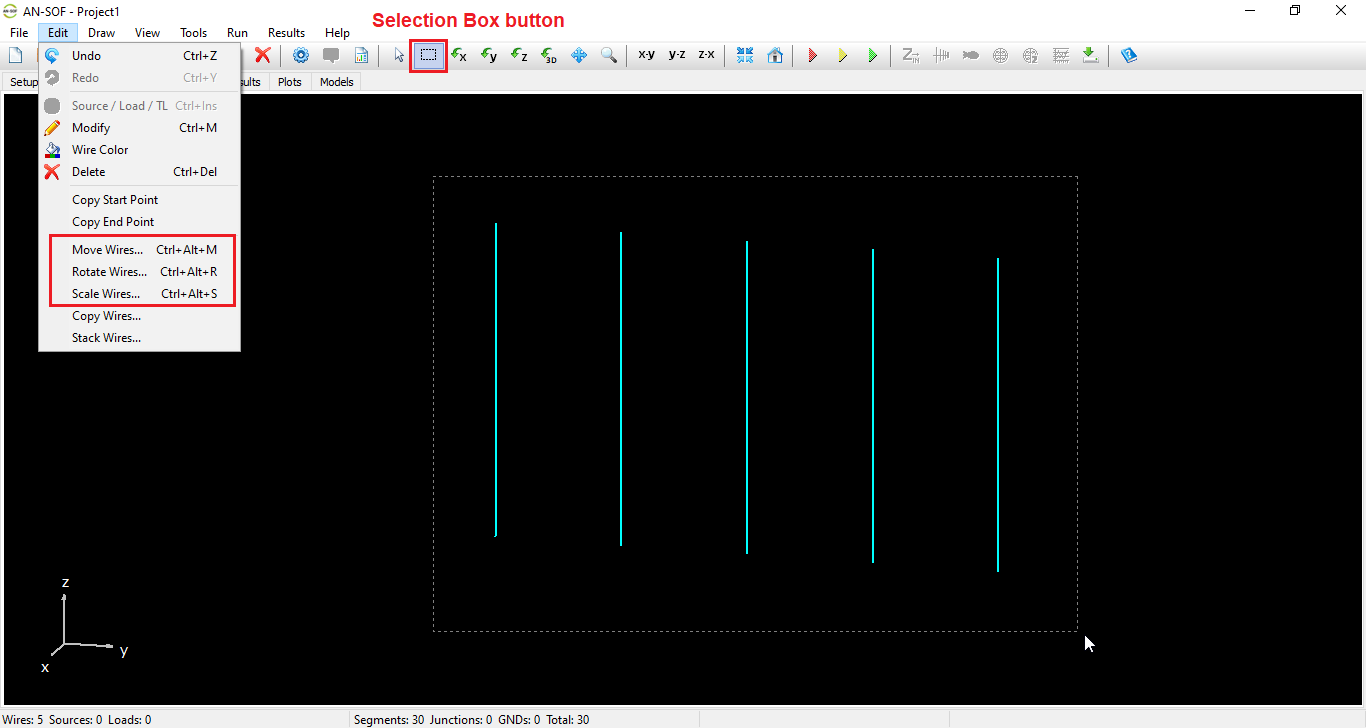
Transforming Selected Wires
Once the wires are selected, navigate to the Edit menu and choose one of the following commands:
Move Wires
Opens the Move Wires dialog box (see Fig. 2), allowing you to move the selected wire or group of wires to a new position. You can specify the shift along the X, Y, and Z coordinates.
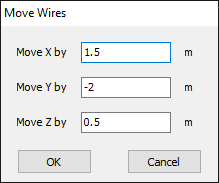
Rotate Wires
Opens the Rotate Wires dialog box (see Fig. 3), enabling you to rotate the selected wire or group of wires around a chosen axis. In addition to the Cartesian axes (X, Y, and Z), the Custom option allows you to define a rotation axis using spherical coordinates (Theta, Phi). You can also set the Rotation Center to rotate around a point other than the origin.
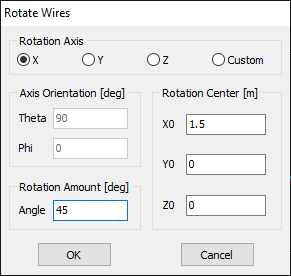
Scale Wires
Opens the Scale Wires dialog box (see Fig. 4), providing the following scaling options:
- Single Factor:
- Apply a single scale factor to all point coordinates of the selected wires.
- Optionally, scale the wire cross-section and coating thickness by the same factor by checking the corresponding boxes.
- Line Length:
- Apply scaling only to linear wires.
- Enter a scale factor and specify an anchored point: the line’s start point (P1) or end point (P2). This allows you to lengthen or shorten the line while keeping one end fixed.
- Advanced:
- Apply different scale factors for each Cartesian coordinate (X, Y, and Z).
- Stretch or contract the selected wires along the direction of one of the Cartesian axes.
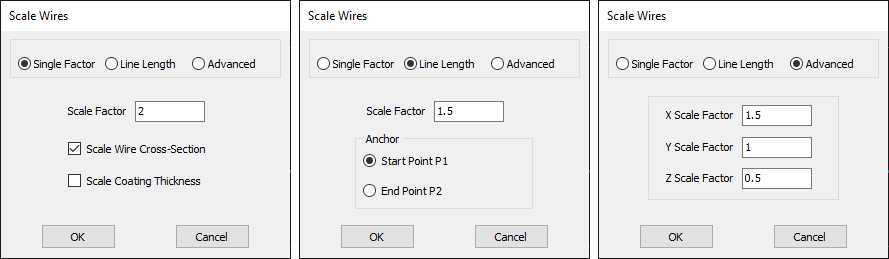
Note
Transmission lines fully enclosed by the selection box will be transformed along with the associated wires when using the Move, Rotate, or Scale transformations in the Edit menu. This ensures that transmission lines remain connected to wires selected via the Selection Box.
When drawing a wire structure, it’s often necessary to copy wires from one position to another—for example, when creating an antenna array. To copy wires, first select them using one of the following methods:
- Click the Selection Box button on the toolbar and drag a box with the mouse to enclose the wires you want to copy (see the Moving, Rotating and Scaling Wires section for details).
- Hold the Ctrl key and left-click on wires to select them individually.
- Combine methods 1 and 2 for more flexible selection.
For a full overview of wire selection techniques, see:
In the Edit menu, you will find the following commands for copying the selected wires:
Copy Wires
Opens the Copy Wires dialog box (see Fig. 1), allowing you to copy the selected wire or group of wires.
- Specify the number of copies of the selected group of wires.
- The first copy will be offset from the original wire group based on the entered X, Y, and Z offsets and/or rotated around each axis according to the entered angles.
- Each subsequent copy will be offset and/or rotated relative to the previous copy.
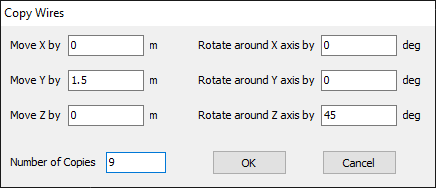
Stack Wires
Opens the Stack Wires dialog box (see Fig. 2), allowing you to stack the selected wire or group of wires along a specified direction.
- Specify the number of elements in the stack. Each “element” consists of the selected wires, which could be a single wire or a group of wires.
- Define the spacing between the elements.
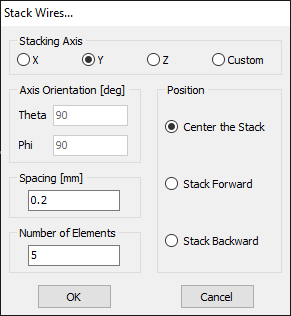
Grids and Surfaces
The grids are wire frameworks with holes on the surface they depict, whereas the surfaces represent solid metal sheets without holes. The wires of a grid do not overlap but are connected to each other. Wires used in grids or surfaces can be straight or curved.
AN-SOF offers various types of grids and surfaces, each with its unique geometric parameters and attributes that can be configured in dedicated Draw dialog boxes.
To access these options, navigate to Draw > Wire Grid / Solid Surface in the main menu, where you will find the following choices:
- Patch: Opens the Draw dialog box for creating a rectangular patch parallel to the xy-plane.
- Plate: Opens the Draw dialog box for creating a plate or bilinear surface.
- Disc: Opens the Draw dialog box for creating a disc.
- Flat Ring: Opens the Draw dialog box for creating a flat ring, which is a disc with a hole at its center.
- Cone: Opens the Draw dialog box for creating a cone.
- Truncated Cone: Opens the Draw dialog box for creating a truncated cone.
- Cylinder: Opens the Draw dialog box for creating a cylinder.
- Sphere: Opens the Draw dialog box for creating a sphere.
- Paraboloid: Opens the Draw dialog box for creating a paraboloid.
Tip
Go to View > Drawing Panel in the main menu to quickly access the wire grids and solid surfaces.
The Attributes page is part of the Draw dialog box for various wire grids and solid surface types. As shown in Fig. 1, this example illustrates the Attributes page for the Plate, but note that all grids and surfaces share the same Attributes page.
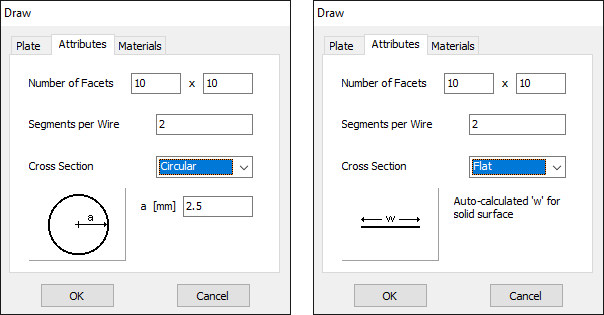
To select between a wire grid or a solid surface, refer to the “Cross-Section” field below. Wire grids consist of wires with a specified circular cross-section, leaving gaps between them, while solid surfaces use flat wires whose width is automatically adjusted to cover the surface without gaps.
On the Attributes page, you can set the following parameters:
Number of Facets
Each grid or surface consists of a specific number of facets. For instance, the plate shown here has a 10×10 arrangement of facets, while the disc here has 6×12 facets. Each facet is a quadrilateral formed by four wires, with each wire divided into segments.
For solid surfaces, the wires are essentially flat strips that cover the entire surface. In the AN-SOF workspace, only the strip axes are displayed. During the simulation process, an unknown current is determined for each wire segment.
You have the flexibility to individually edit any curved or straight wire that comprises a grid or surface. Refer to Modifying a Wire for details on editing individual wires. If you need to make mass edits to the wires that make up a grid or surface, please refer to Modifying a Grid/Surface.
In the case of a Patch, setting the number of facets to 0x0 results in an automatic calculation. The calculation considers 10 segments per wavelength along each side of the patch, with the wavelength corresponding to the highest frequency defined.
Segments per Wire
This parameter determines the number of segments for each wire within the grid/surface. If “Segments per Wire” is set to zero, each wire will be automatically divided into segments, with the calculation based on a default value of 10 segments per wavelength.
Please note that the Patch type does not offer the option to specify “Segments per Wire” since its facets are composed of one-segment wires and the number of facets can be automatically computed by setting 0x0 facets.
Cross-Section
To define a wire grid, choose a Circular cross-section and set the radius of the wires comprising the grid, as shown in Fig. 1 on the left. Wire grids cannot have infinitesimally thin wires, so the cross-section radius “a” must be greater than zero.
To define a solid surface, select either the Flat or Rectangular cross-section for the wires that constitute the surface, as shown in Fig. 1 on the right. These wires are essentially flat strips that completely cover the surface. With the ‘Rectangular’ cross-section option, you can specify the thickness of the solid surface.
A grid or surface can be modified using the procedure described in Modifying a Group of Wires. To select multiple wires, wire grids, or solid surfaces, click on the Selection Box button on the main toolbar. Left-click on the workspace, drag the mouse to create a selection box, and all wires within it will be highlighted in light blue, as shown in Fig. 1.
To apply modifications to the selected wires, go to Edit > Modify (you can also use the shortcut Ctrl + M), or use the Modify button on the toolbar. This command becomes active when you have a group of wires, a wire grid, or a solid surface selected. For details on the dialog window that allows you to modify selected wires, please refer to Modifying a Group of Wires.
If you need to perform actions such as moving, rotating, scaling, copying, or stacking wire grids and solid surfaces, please consult Moving, Rotating and Scaling Wires and Copying and Stacking Wires for more information.
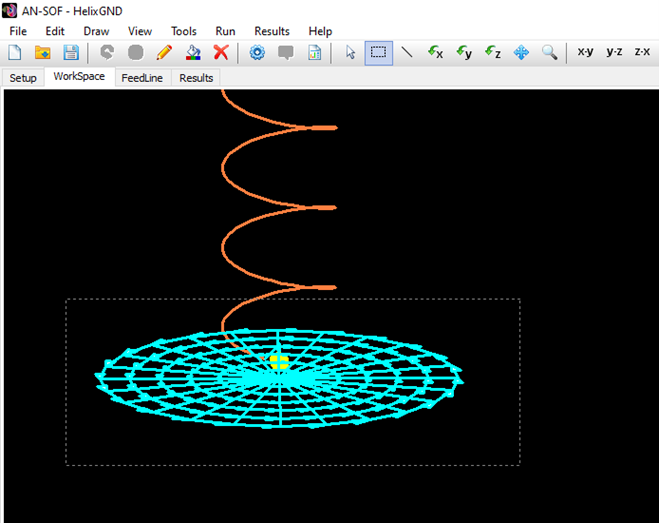
Click on the Selection Box button in the main toolbar. By left-clicking on the workspace and dragging a box with the mouse, you can select a wire grid or a solid surface, as explained in Modifying a Grid/Surface or Modifying a Group of Wires. All wires inside the selection box will be highlighted in light blue.
Go to Edit > Delete (Ctrl + Del) in the main menu to delete the selected grid or surface. There is also a button on the toolbar with the Delete command. This command is enabled when a group of wires, a wire grid, or a solid surface is selected.
Click on the Selection Box button in the main toolbar. By left-clicking on the workspace and dragging a box with the mouse, you can select a wire grid or a solid surface, as explained in Modifying a Grid/Surface or Modifying a Group of Wires. All wires inside the selection box will be highlighted in light blue.
Go to Edit > Wire Color in the main menu to change the color of the selected grid or surface. A dialog window will be opened where a color can be chosen. There is also a button on the toolbar with the Wire Color command. This command is enabled when a group of wires, a wire grid, or a solid surface is selected.
Adding Wire Grids/Solid Surfaces
A Patch in AN-SOF represents a solid rectangular conductive surface lying on the xy-plane or a plane parallel to it (z = constant). This structure consists of wires with a flat or rectangular cross-section that cover the entire surface of the patch.
You can use this command to model patch antennas, where the patch is a solid rectangular metal sheet. To do this, you must choose the Substrate option as the ground plane by navigating to the Setup tab > Environment panel > Ground Plane box.
If you need to model a solid rectangular surface or a rectangular wire grid in free space or above a real ground plane, use the Plate command instead of Patch.
To access the Patch command, go to Draw > Wire Grid / Solid Surface > Patch in the main menu. The displayed dialog box consists of three pages: Patch, Attributes, and Materials, detailed in Fig. 1.
The Patch page
On the Patch page, you can configure the geometric parameters for the Patch. To define the Patch, specify the coordinates of two opposite corner points in a plane z = constant, as illustrated in Fig. 2.
Once you’ve configured the geometric parameters on the Patch page, you can proceed to the Attributes page, where you can specify the number of facets for the Patch. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
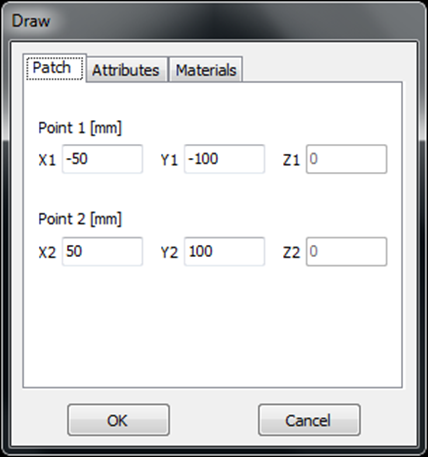
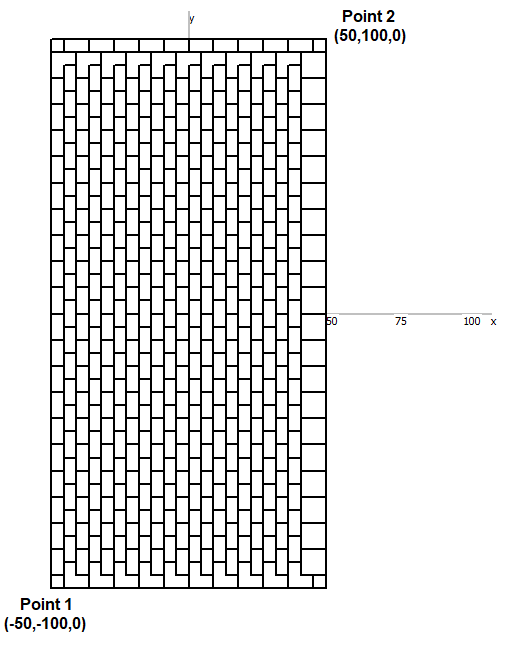
The Plate command refers to a plate or bilinear surface.
To access the Plate command, go to Draw > Wire Grid / Solid Surface > Plate in the main menu. The dialog box for the Plate command contains three pages: Plate, Attributes, and Materials, detailed in Fig. 1.
The Plate page
In the Plate page, you can set the geometrical parameters for the Plate. The Plate is defined by specifying the coordinates of its four corner points. In general, a plate or bilinear surface is a non-planar quadrilateral, uniquely defined by its four vertices, as shown in Fig. 2. In some cases, the bilinear surface degenerates into a flat quadrilateral.
After setting the geometrical parameters on the Plate page, you can move on to the Attributes page. Here, you can specify the number of facets for the Plate and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
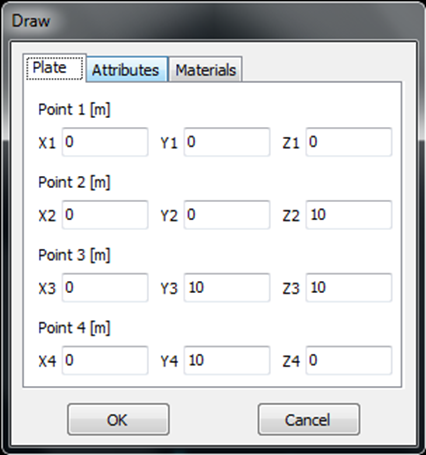
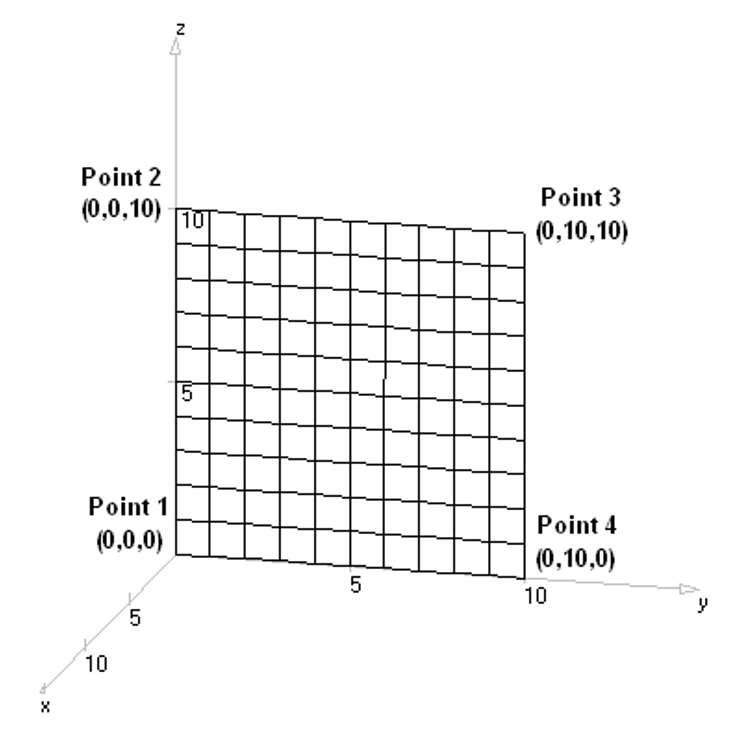
The Disc command is used to create a disc or circular surface.
To access this command, go to Draw > Wire Grid / Solid Surface > Disc in the main menu. This action will open the Draw dialog box for the Disc. The dialog box consists of three pages: Disc, Attributes, and Materials, as detailed in Fig. 1.
The Disc page
In the Disc page, you can configure the geometrical parameters for the Disc. Here, you’ll find a combo-box offering two options: Curved segments and Straight segments. Select Curved segments for an exact representation of the disc’s curvature. The Straight segments option provides an approximation using linear wires.
The Disc is defined by specifying the Center coordinates, Radius, and orientation angles, Theta and Phi. These parameters uniquely define a planar disc surface, as illustrated in Fig. 2.
After setting the geometrical parameters on the Disc page, you can move on to the Attributes page. Here, you can specify the number of facets for the Disc and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
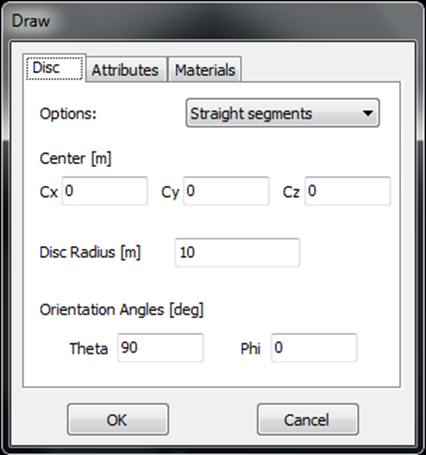
Disc Equivalent Radius Calculator
The Flat Ring command creates a disc with a hole at its center.
To access this command, go to Draw > Wire Grid / Solid Surface > Flat Ring in the main menu. This action opens the Draw dialog box for the Flat Ring. The dialog box comprises three pages: Flat Ring, Attributes, and Materials, detailed in Fig. 1.
The Flat Ring page
On the Flat Ring page, you can specify the geometrical parameters for the Flat Ring. Here, you’ll find a combo-box offering two options: Curved segments and Straight segments. Choose Curved segments for an exact representation of the flat ring’s curvature. The Straight segments option provides an approximation using linear wires.
The Flat Ring is defined by providing the Center coordinates, Inner Radius (hole radius), Outer Radius, and orientation angles, Theta and Phi. These parameters uniquely define a planar flat ring surface, as illustrated in Fig. 2.
After setting the geometrical parameters on the Flat Ring page, you can move on to the Attributes page. Here, you can specify the number of facets for the Flat Ring and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
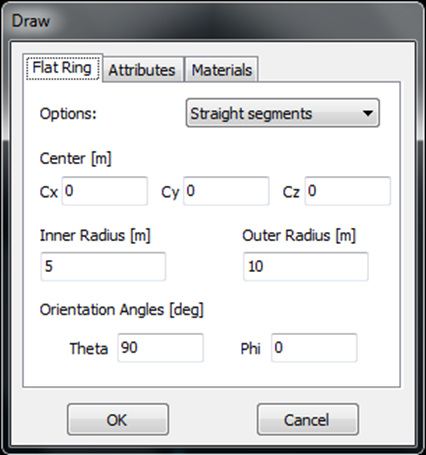
Ring Equivalent Radii Calculator
The Cone command creates a cone-shaped structure.
To access this command, go to Draw > Wire Grid / Solid Surface > Cone in the main menu, which opens the Draw dialog box for the Cone. The dialog box comprises three pages: Cone, Attributes, and Materials, as detailed in Fig. 1.
The Cone page
On the Cone page, you can set the geometrical parameters for the Cone. You’ll find a combo-box with two options: Curved segments and Straight segments. Choose Curved segments for an exact representation of the cone’s curvature, while the Straight segments option provides an approximation using linear wires.
The Cone is defined by specifying the Vertex coordinates, Aperture Angle, Aperture Radius, and orientation angles, Theta and Phi. These parameters uniquely define the cone’s surface, as illustrated in Fig. 2.
After setting the geometrical parameters on the Cone page, you can move on to the Attributes page. Here, you can specify the number of facets for the Cone and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
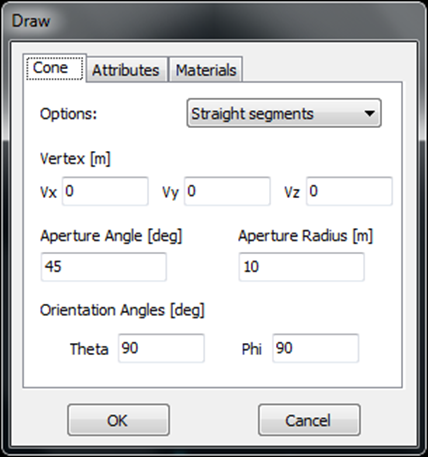
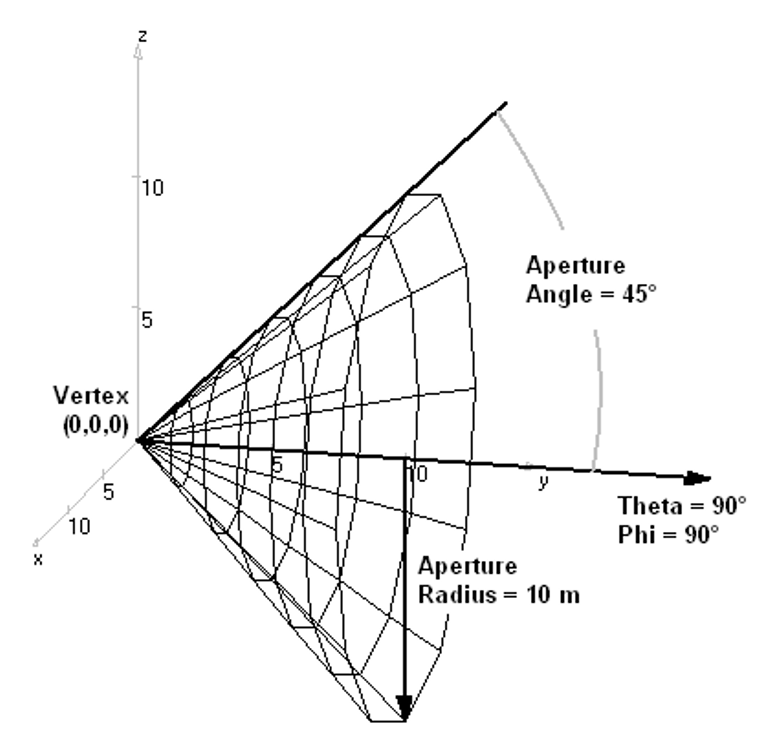
The Truncated Cone command creates a truncated cone-shaped structure.
To access this command, go to Draw > Wire Grid / Solid Surface > Truncated Cone in the main menu, which opens the Draw dialog box for the Truncated Cone. The dialog box comprises three pages: Truncated Cone, Attributes, and Materials, as detailed in Fig. 1.
The Truncated Cone page
On the Truncated Cone page, you can set the geometrical parameters for the Truncated Cone. You’ll find a combo-box with two options: Curved segments and Straight segments. Choose Curved segments for an exact representation of the truncated cone’s curvature, while the Straight segments option provides an approximation using linear wires.
The Truncated Cone is defined by specifying the Base Point coordinates, Base Radius, Top Radius, Aperture angle, and orientation angles, Theta and Phi. These parameters uniquely define the truncated cone’s surface, as illustrated in Fig. 2. Depending on its parameters, a truncated cone can take on various shapes, including a cylinder, a cone, a disc, or a flat ring.
After setting the geometrical parameters on the Truncated Cone page, you can move on to the Attributes page. Here, you can specify the number of facets for the Truncated Cone and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
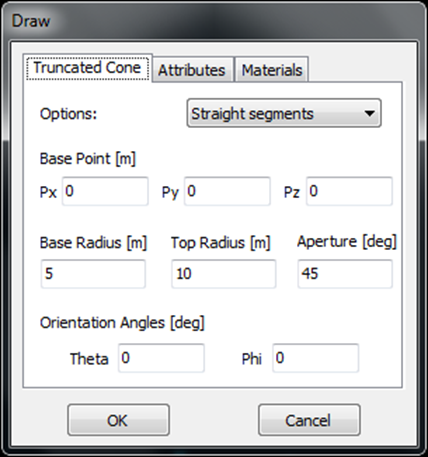
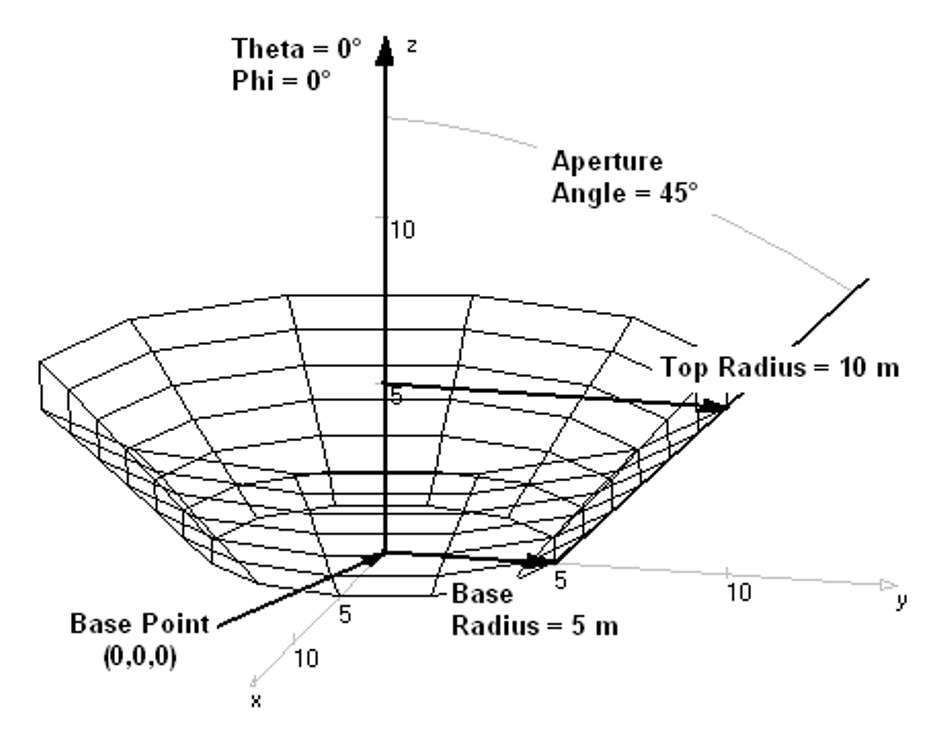
The Cylinder command creates a cylindrical structure.
To access this command, go to Draw > Wire Grid / Solid Surface > Cylinder in the main menu, which opens the Draw dialog box for the Cylinder. The dialog box comprises three pages: Cylinder, Attributes, and Materials, as detailed in Fig. 1.
The Cylinder page
On the Cylinder page, you can set the geometrical parameters for the Cylinder. You’ll find a combo-box with two options: Curved segments and Straight segments. Choose Curved segments for an exact representation of the cylinder’s curvature, while the Straight segments option provides an approximation using linear wires.
The Cylinder is defined by specifying the Base Point coordinates, Length, Radius, and orientation angles, Theta and Phi. These parameters uniquely define the cylinder’s surface, as illustrated in Fig. 2.
After setting the geometrical parameters on the Cylinder page, you can move on to the Attributes page. Here, you can specify the number of facets for the Cylinder and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
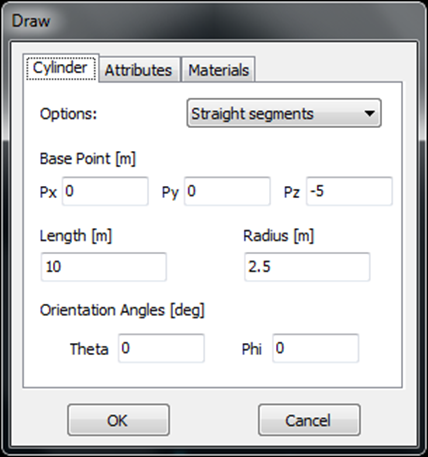
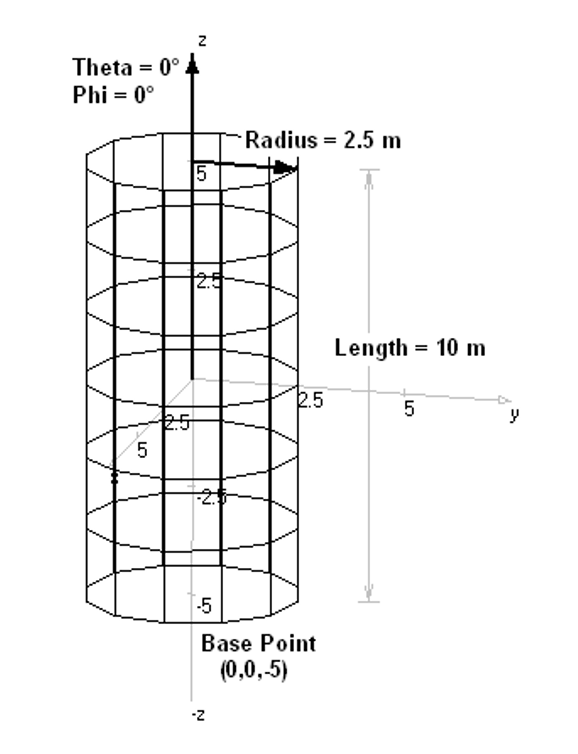
The Sphere command creates a spherical structure.
To access this command, go to Draw > Wire Grid / Solid Surface > Sphere in the main menu, which opens the Draw dialog box for the Sphere. The dialog box comprises three pages: Sphere, Attributes, and Materials, as detailed in Fig. 1.
The Sphere page
On the Sphere page, you can set the geometrical parameters for the Sphere. You’ll find a combo-box with two options: Curved segments and Straight segments. Choose Curved segments for an exact representation of the sphere’s curvature, while the Straight segments option provides an approximation using linear wires.
The Sphere is defined by specifying the Center coordinates, Radius, and orientation angles, Theta and Phi. These parameters uniquely define the sphere’s surface, as shown in Fig. 2.
After setting the geometrical parameters on the Sphere page, you can move on to the Attributes page. Here, you can specify the number of facets for the Sphere and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
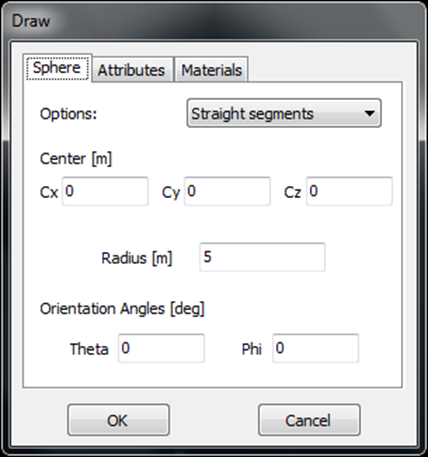
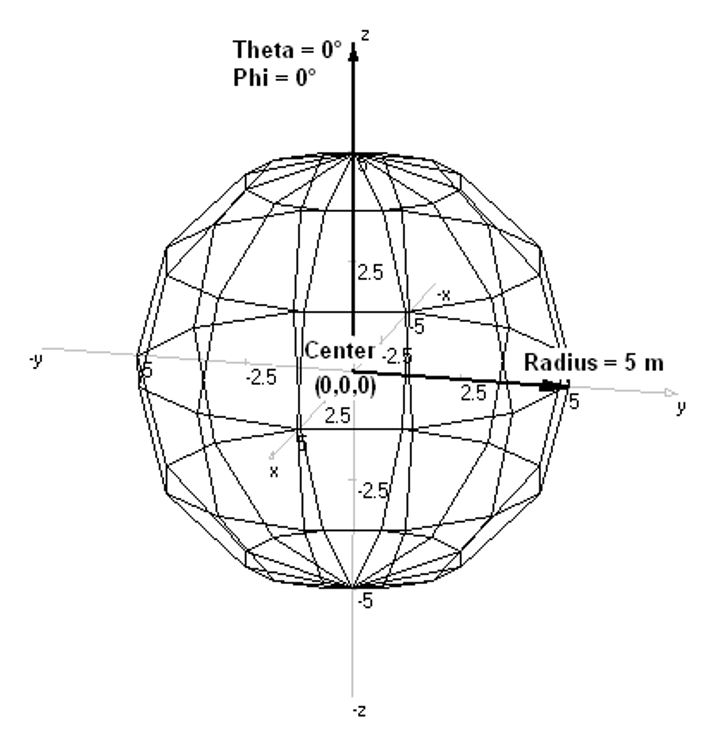
The Paraboloid command creates a paraboloidal structure.
To access this command, go to Draw > Wire Grid / Solid Surface > Paraboloid in the main menu, which opens the Draw dialog box for the Paraboloid. The dialog box comprises three pages: Paraboloid, Attributes, and Materials, as detailed in Fig. 1.
The Paraboloid page
On the Paraboloid page, you can set the geometrical parameters for the Paraboloid. You’ll find a combo-box with two options: Curved segments and Straight segments. Choose Curved segments for an exact representation of the paraboloid’s curvature, while the Straight segments option provides an approximation using linear wires.
The Paraboloid is defined by specifying the Vertex coordinates, Focal Distance, Aperture Radius, and orientation angles, Theta and Phi. These parameters uniquely define the paraboloid’s curved surface, as shown in Fig. 2.
After setting the geometrical parameters on the Paraboloid page, you can move on to the Attributes page. Here, you can specify the number of facets for the Paraboloid and choose whether it should be a wire grid or a solid surface. See Grid/Surface Attributes for additional parameters in the Attributes page and Wire Materials for parameters in the Materials page.
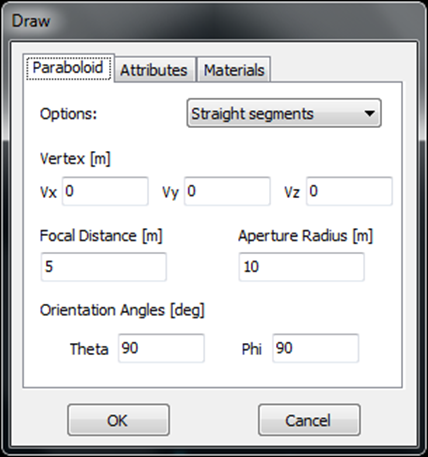
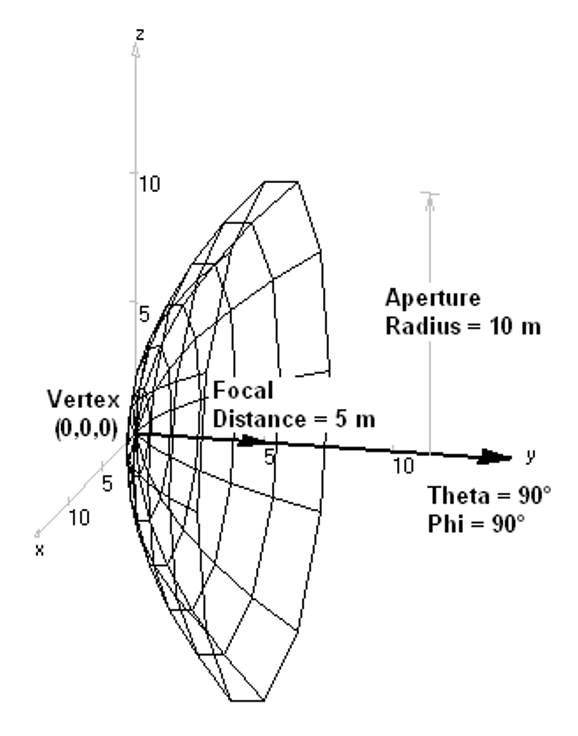
Sources and Loads
Discrete Sources, Incident Field, and Loads
A structure in AN-SOF can be excited either by discrete sources or by an incident electromagnetic field. For the latter, refer to Excitation by an Incident Field. Discrete sources can be placed on any wire segment, and multiple sources may be added—up to one per segment if needed.
A source represents the feed point of a transmitting antenna or an electrical generator. There are two types of sources:
- Voltage sources
- Current sources (used to model impressed currents)
For each source, you must define its amplitude and phase. Additionally, you can assign an internal impedance to simulate non-ideal sources. The impedance can take one of the following forms:
- Series RL (inductive)
- Series RC (capacitive)
- Fixed complex impedance (R + jX)
In addition to sources, lumped loads can be inserted into any wire segment to model passive components or matching circuits. Six types of loads are available:
- Series RL impedance (inductive)
- Series RC impedance (capacitive)
- Fixed R + jX impedance (reactance does not scale with frequency)
- Series RLC circuit
- Parallel RLC circuit
- Trap RLC circuit
To model a pure resistor, set an inductive load with L = 0.
Note:
You can set the units for inductance and capacitance in Main Menu > Tools > Preferences. Supported units include:
• Inductance: pH, nH, µH, mH, H
• Capacitance: pF, nF, µF, mF, F
In the 3D workspace:
- Sources are represented by a yellow circle
- Loads are indicated by a green-highlighted wire segment (see Fig. 1)
Tips
- To customize the default colors of sources and loads, go to: Main Menu > Tools > Preferences > Workspace tab.
- To change the size of the source displayed in the workspace, go to Main Menu > Tools > Preferences > Workspace tab, and adjust the Source Size % setting.
- Voltage sources have their internal impedance in series.
To model an ideal (perfect) voltage source, set the impedance to zero.
- Current sources have their internal impedance in parallel.
To approximate an ideal current source, use a very high impedance (e.g., 1 MΩ).
Excitation by Sources
To excite the wire structure using discrete sources, go to the Setup tab, open the Excitation panel, and select the Discrete Sources option (see Fig. 2).
If the Set Input Power option is enabled, you can specify the total input power delivered to the structure. In this case, the amplitudes of the voltage and current sources will be automatically adjusted to match the desired input power.
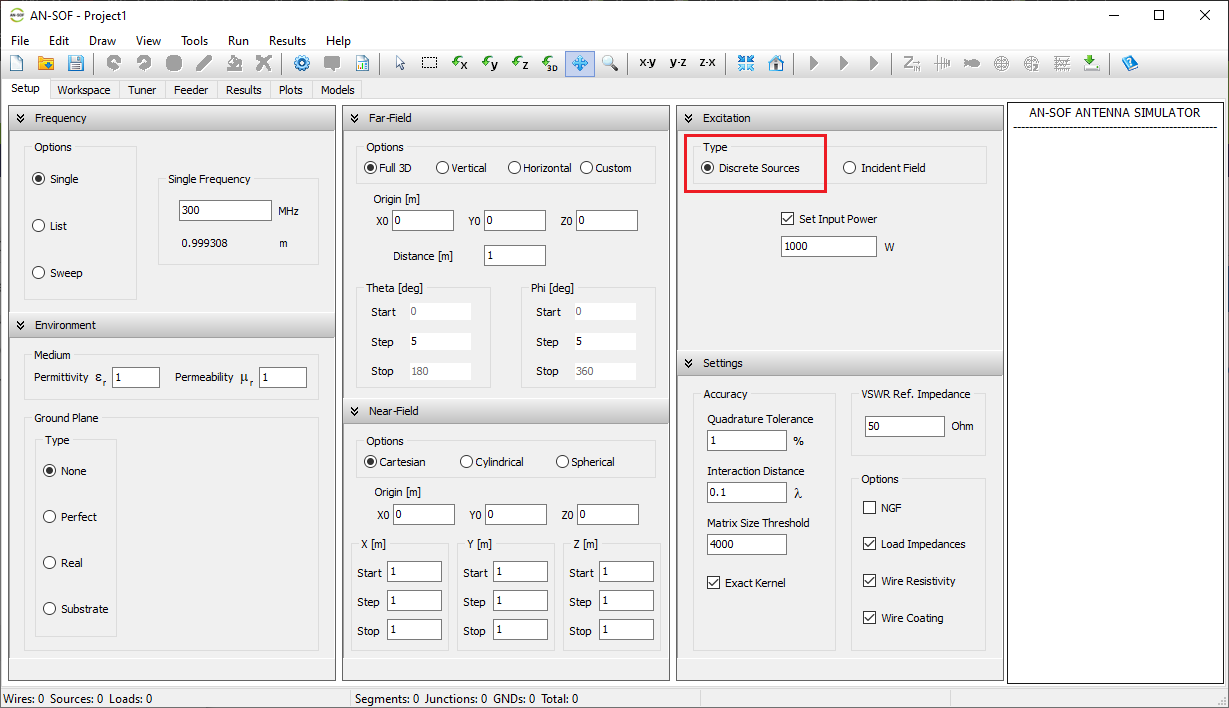
To add a source to a wire segment, first right-click on the desired wire and select “Source / Load / TL (Ctrl + Ins)” from the pop-up menu. A toolbar will appear at the bottom of the screen. Use the slider on this toolbar to select the specific wire segment where you want to place the source.
For more details, see The Source/Load/TL Toolbar.
The Source/Load/TL toolbar is used to connect a source, load, or transmission line to a specific segment of a wire. It also provides tools to edit or remove existing connections.
Accessing the Toolbar
To open this toolbar:
- Right-click on any part of a wire and select Source / Load / TL (Ctrl + Ins) from the pop-up menu (Fig. 1).
- Alternatively, use the main toolbar or go to Edit > Source / Load / TL (Ctrl + Ins) from the main menu. Before using this command, click the Select Wire button (arrow icon on the main toolbar), then left-click the wire where you want to place the source or load.

Toolbar Components
Slider
- The slider lets you choose a specific wire segment.
- Each slider position corresponds to a segment along the selected wire.
- On the right side of the toolbar, you’ll see:
- The segment number.
- The segment’s relative position (in %) along the wire, measured from the wire’s starting point to the midpoint of the selected segment:
Segment Position % = 100 × (segment position / wire length)
50% Button
- Quickly positions the slider at the center of the wire.
- Useful for placing sources or loads at the midpoint.
⚠️ Note: The wire must have an odd number of segments for an exact center segment to exist.
Add Source Button
- Opens a dialog box to add a source to the selected segment (Fig. 2).
- You can specify:
- Source type
- Amplitude
- Phase
- Internal impedance Zs
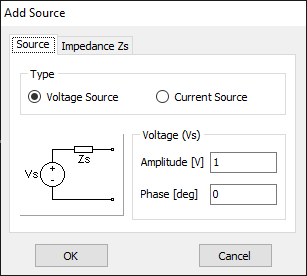
- Voltage sources have their internal impedance in series. To model an ideal (perfect) voltage source, set the impedance to zero.
- Current sources have their internal impedance in parallel. To approximate an ideal current source, use a very high impedance (e.g., 1 MΩ = 1E6 Ohm).
- To change the size of the source displayed in the workspace, go to Main Menu > Tools > Preferences > Workspace tab, and adjust the Source Size % setting.
- To customize the default color of sources, go to: Main Menu > Tools > Preferences > Workspace tab.
Add Load Button
- Opens a dialog to add a load to the selected segment (Fig. 3).
- Load types include:
- Series RL (resistor + inductor)
- Series RC (resistor + capacitor)
- Fixed R + jX impedance (non-frequency-dependent reactance)
- Series or parallel RLC
- Trap (series RL + parallel C)
- To customize the default color of loads, go to: Main Menu > Tools > Preferences > Workspace tab.
Transmission Lines Button
- Opens a dialog to connect a transmission line to the selected segment.
- See the section Adding Transmission Lines for more information.
Delete Button
- Removes any existing source or load from the selected segment.
Modify Button
- Opens a dialog to edit the source or load on the selected segment.
Exit Button
- Closes the Source/Load/TL toolbar.
To add a source to a specific wire segment, follow these steps:
- Right-click on any part of the wire to open the pop-up menu.
- Select Source / Load / TL (Ctrl + Ins) to open the Source / Load / TL toolbar at the bottom of the screen (Fig. 1).
- Use the slider to choose the wire segment where the source will be placed.
- Click the Add Source button to open the Add Source dialog box (Fig. 2).
- Specify the type of source, its amplitude (rms value), phase, and internal impedance, then click OK.
- Click Exit to close the Source / Load / TL toolbar.
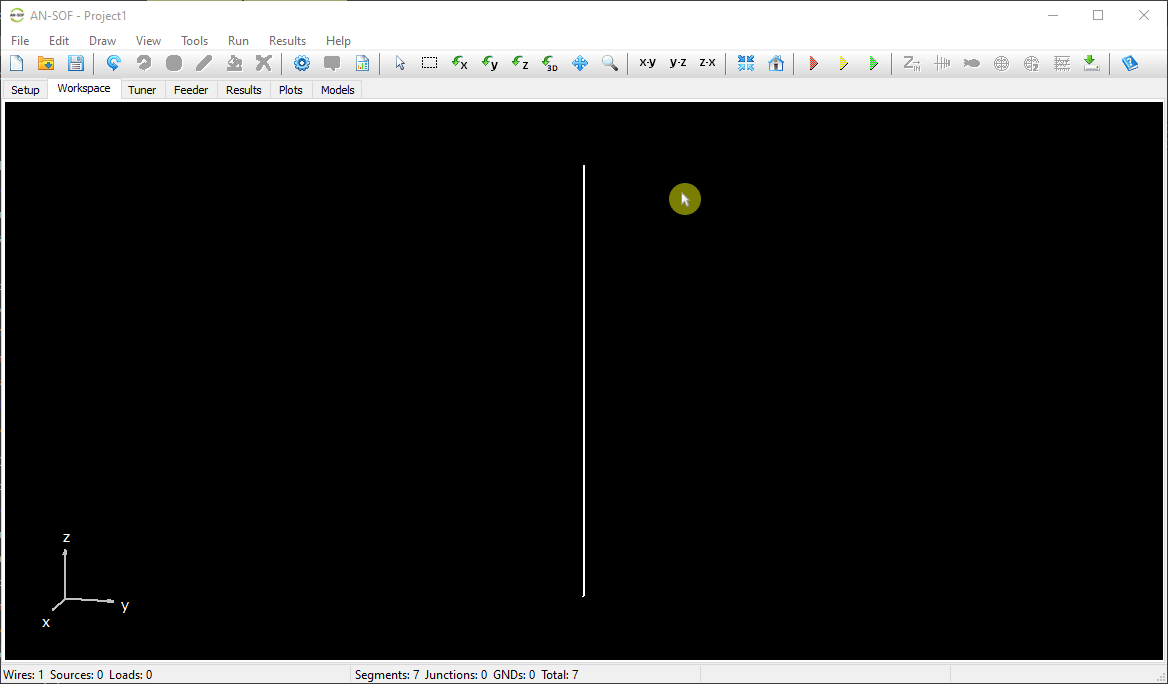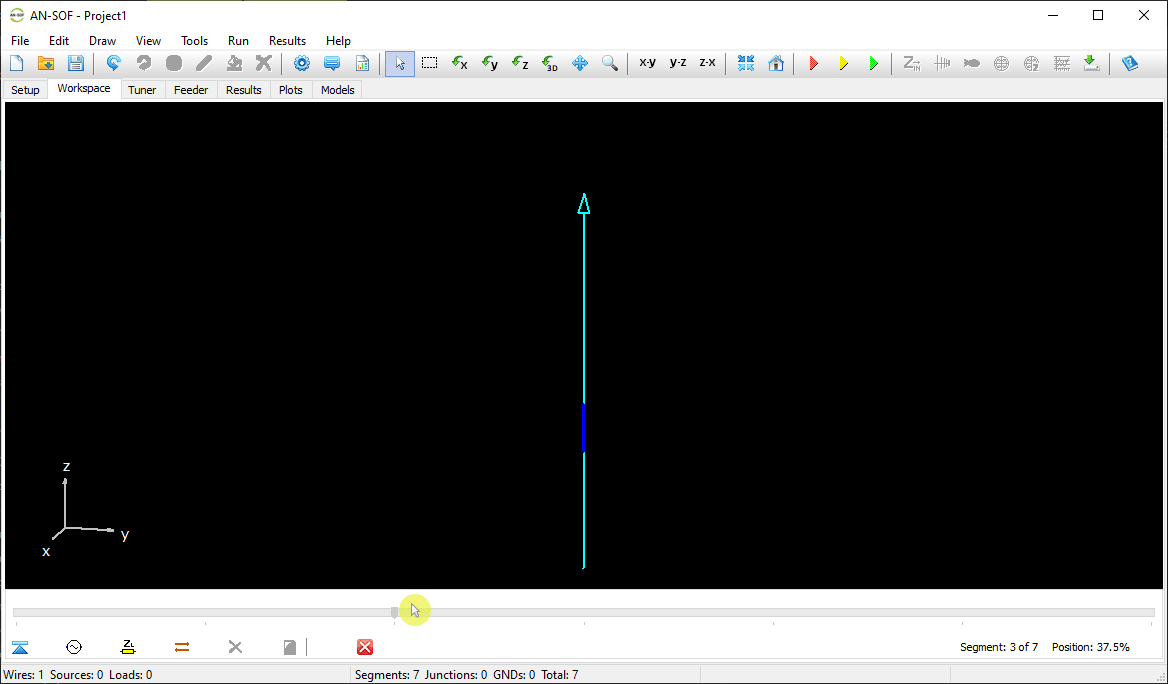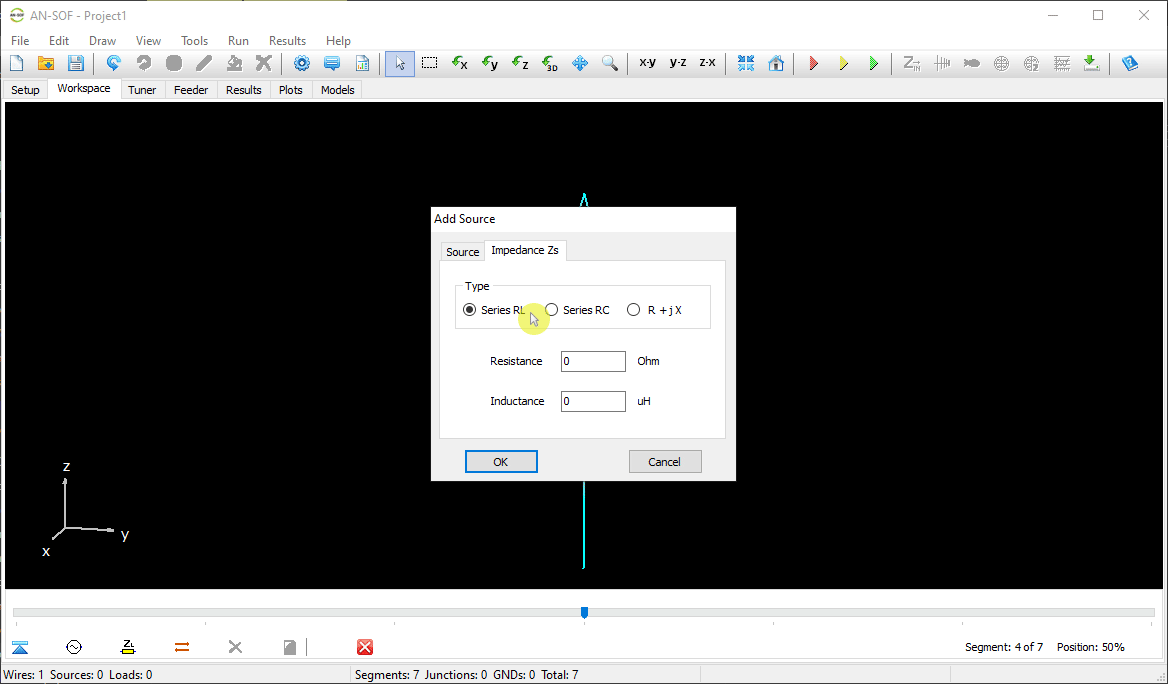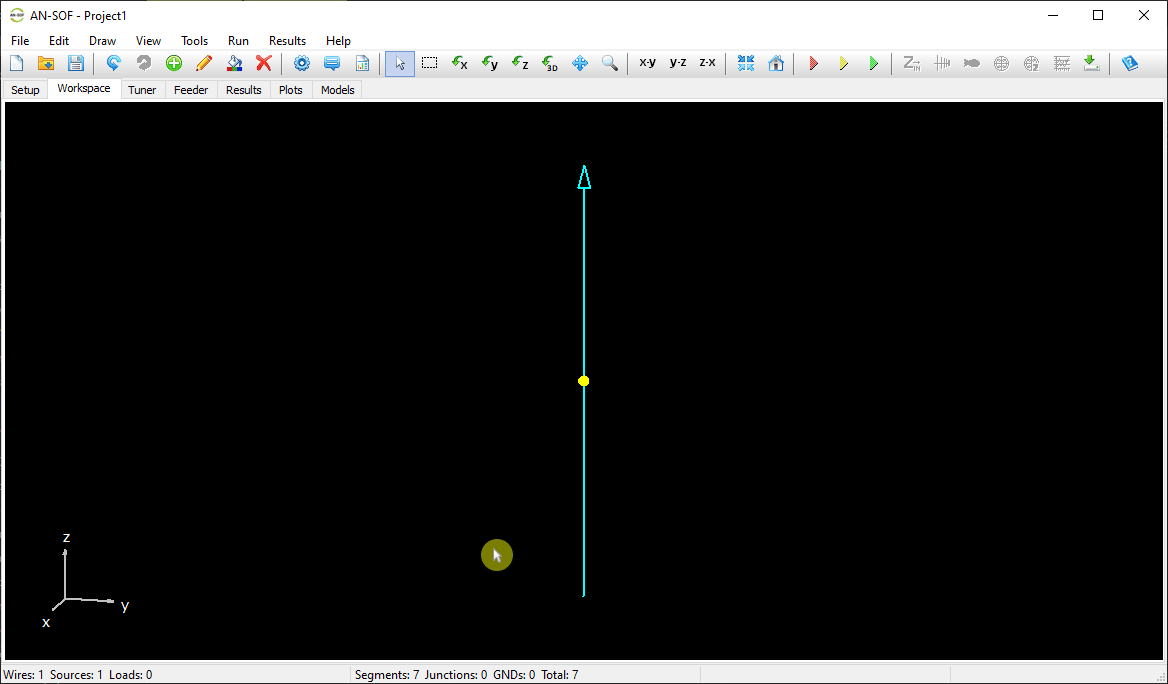

Tips
- To customize the default color of sources, go to: Main Menu > Tools > Preferences > Workspace tab.
- To change the size of the source displayed in the workspace, go to Main Menu > Tools > Preferences > Workspace tab, and adjust the Source Size % setting.
- Voltage sources have their internal impedance in series.
To model an ideal (perfect) voltage source, set the impedance to zero.
- Current sources have their internal impedance in parallel.
To approximate an ideal current source, use a very high impedance (e.g., 1 MΩ = 1E6 Ohm).
To edit an existing source on a wire segment, follow these steps:
- Right-click on any part of the wire to open the pop-up menu.
- Select the Source / Load / TL (Ctrl + Ins) command to open the Source/Load/TL toolbar (Fig. 1).
- Use the slider to locate the segment where the source is placed.
- Click the Modify button to open a dialog box where you can edit the source parameters.
- To remove the source, click the Delete button.
- Click the Exit button to close the Source / Load / TL toolbar.
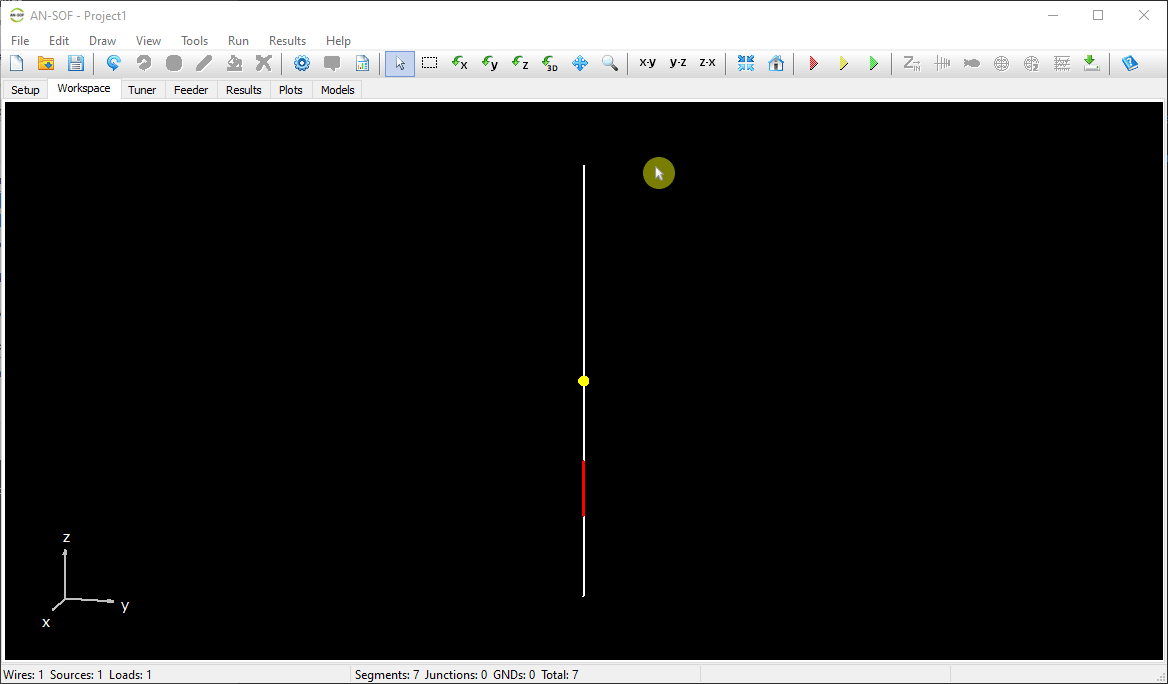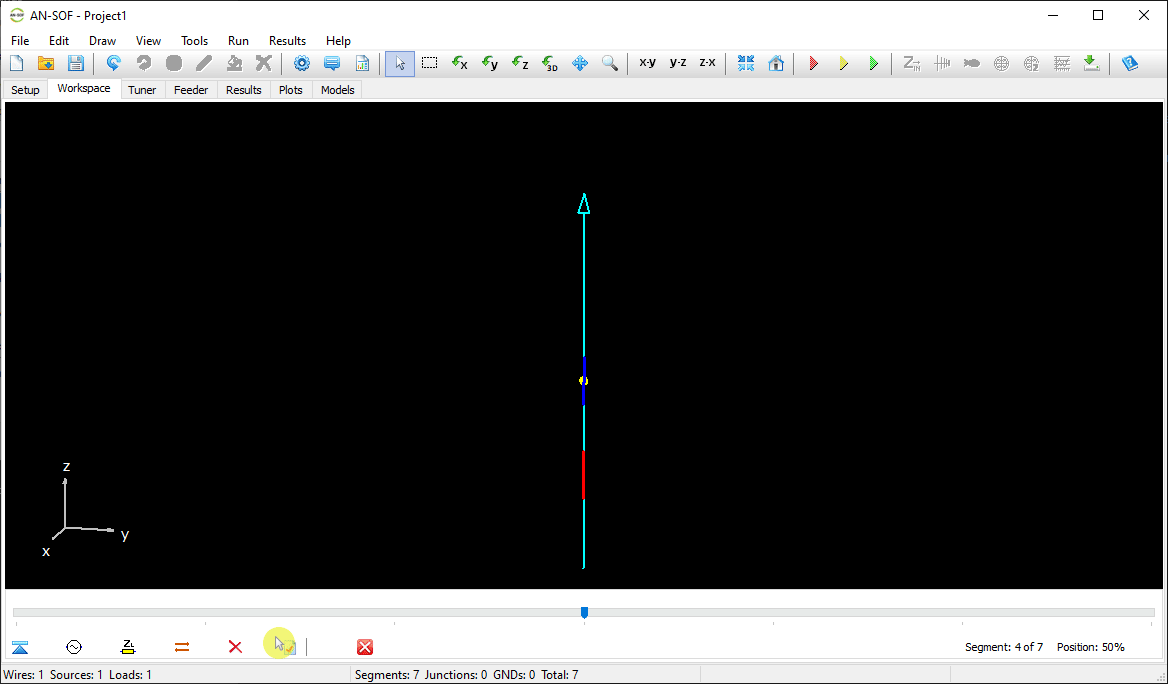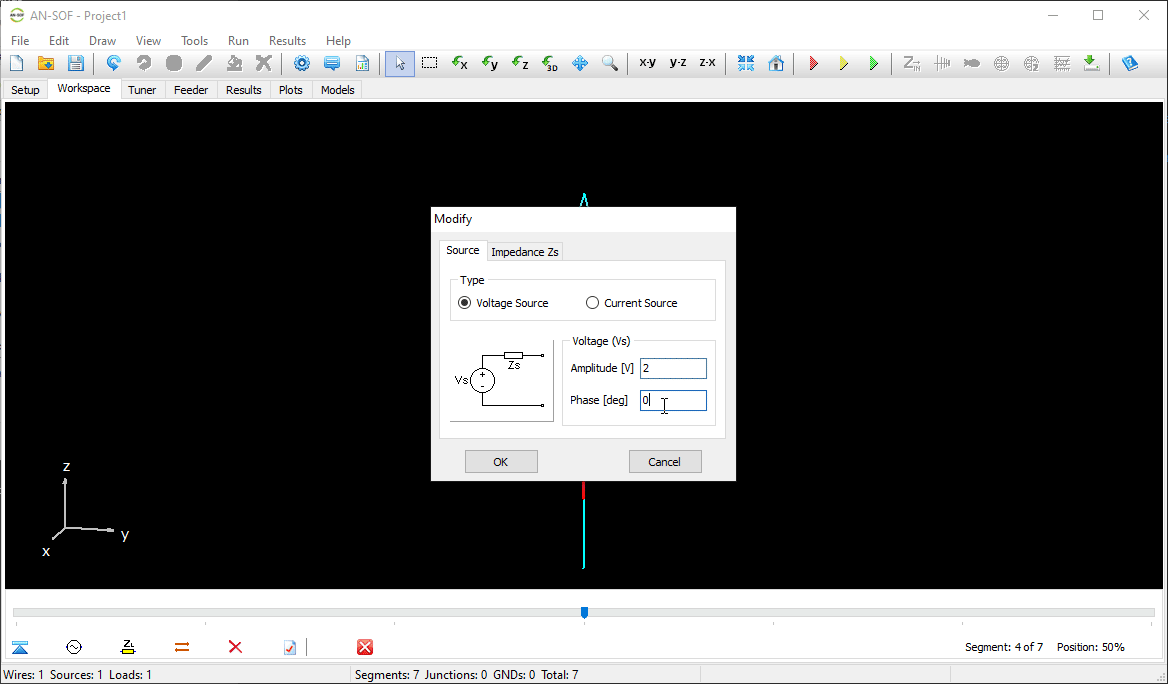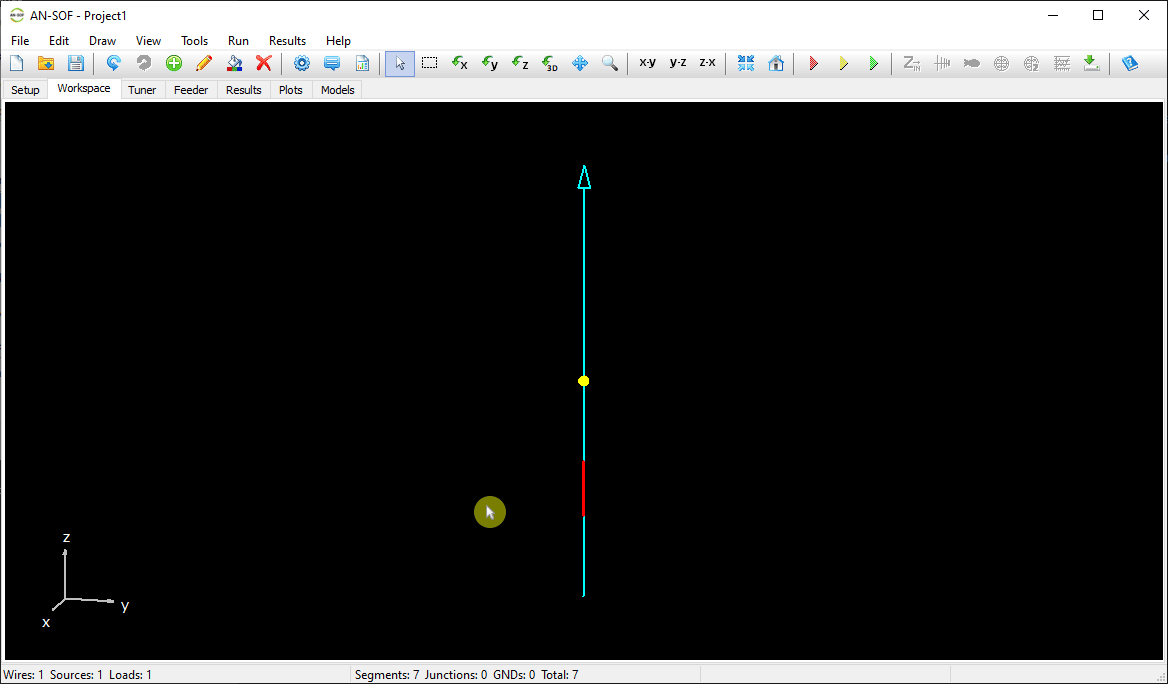
Tips
- To customize the default color of sources, go to: Main Menu > Tools > Preferences > Workspace tab.
- To change the size of the source displayed in the workspace, go to Main Menu > Tools > Preferences > Workspace tab, and adjust the Source Size % setting.
- Voltage sources have their internal impedance in series.
To model an ideal (perfect) voltage source, set the impedance to zero.
- Current sources have their internal impedance in parallel.
To approximate an ideal current source, use a very high impedance (e.g., 1 MΩ = 1E6 Ohm).
To add a load to a selected wire segment, follow these steps:
- Right-click on any part of the wire to display the pop-up menu.
- Select the Source / Load / TL (Ctrl + Ins) command from the menu to open the Source / Load / TL toolbar (Fig. 1) at the bottom of the screen.
- Use the slider on the toolbar to select the desired wire segment.
- Click the Add Load button to open the Add Load dialog box (Fig. 2).
- Specify the load type, along with the required RLC values, then click OK.
- Click the Exit button to close the Source/Load/TL toolbar.
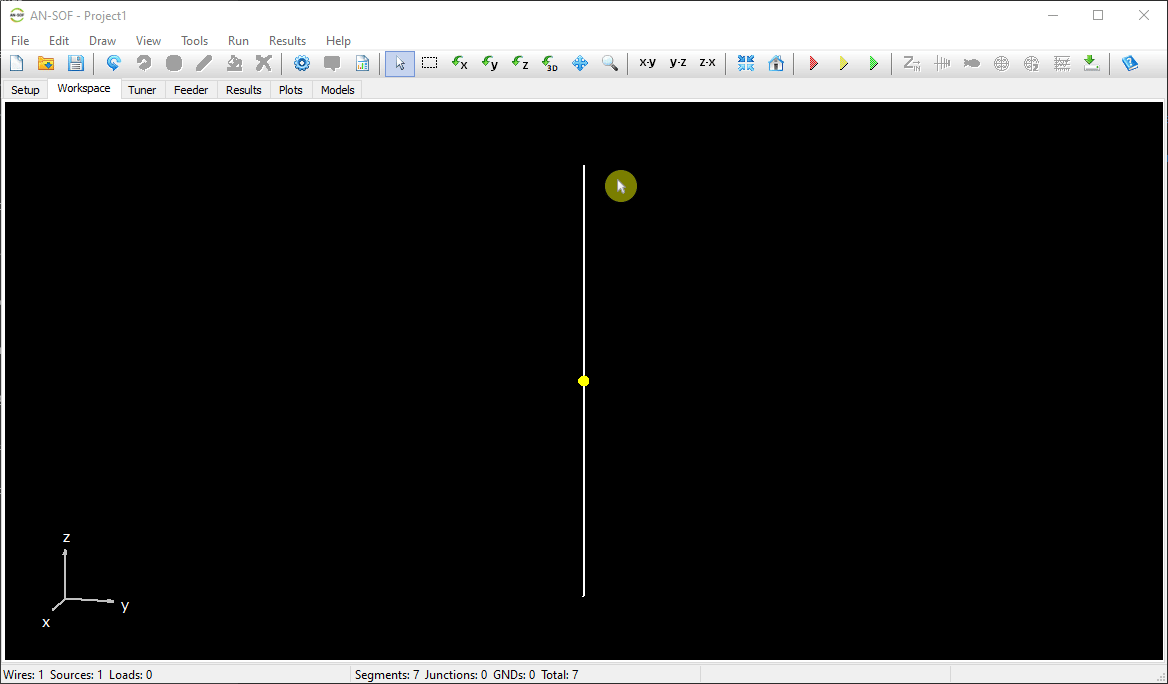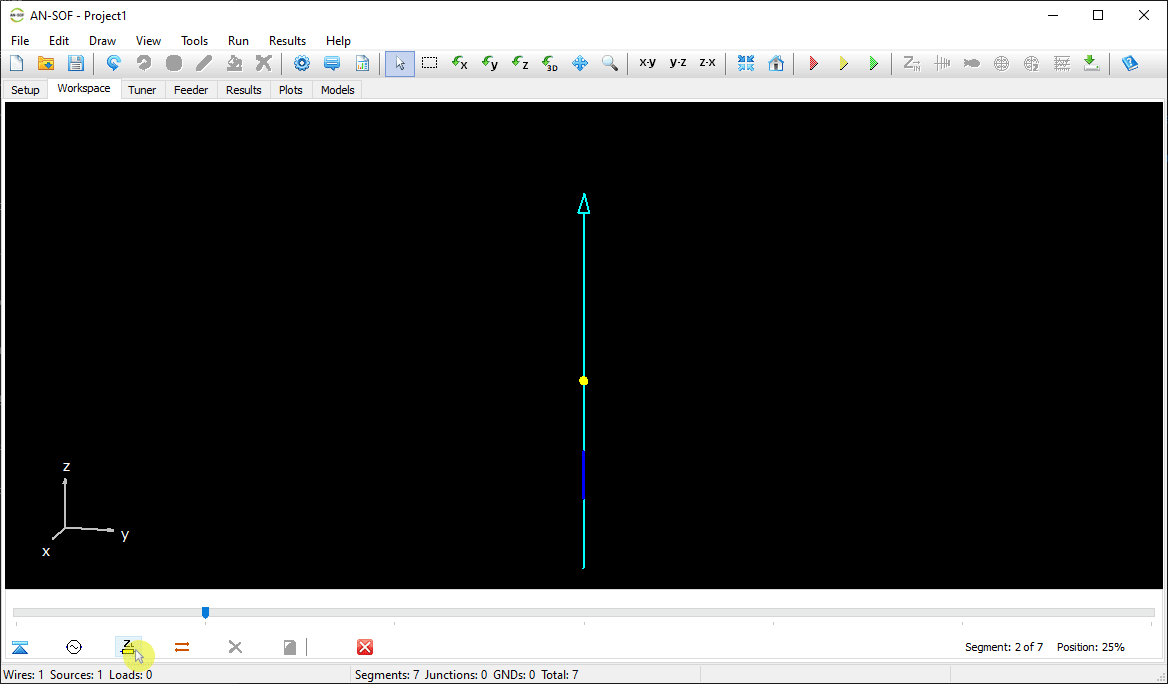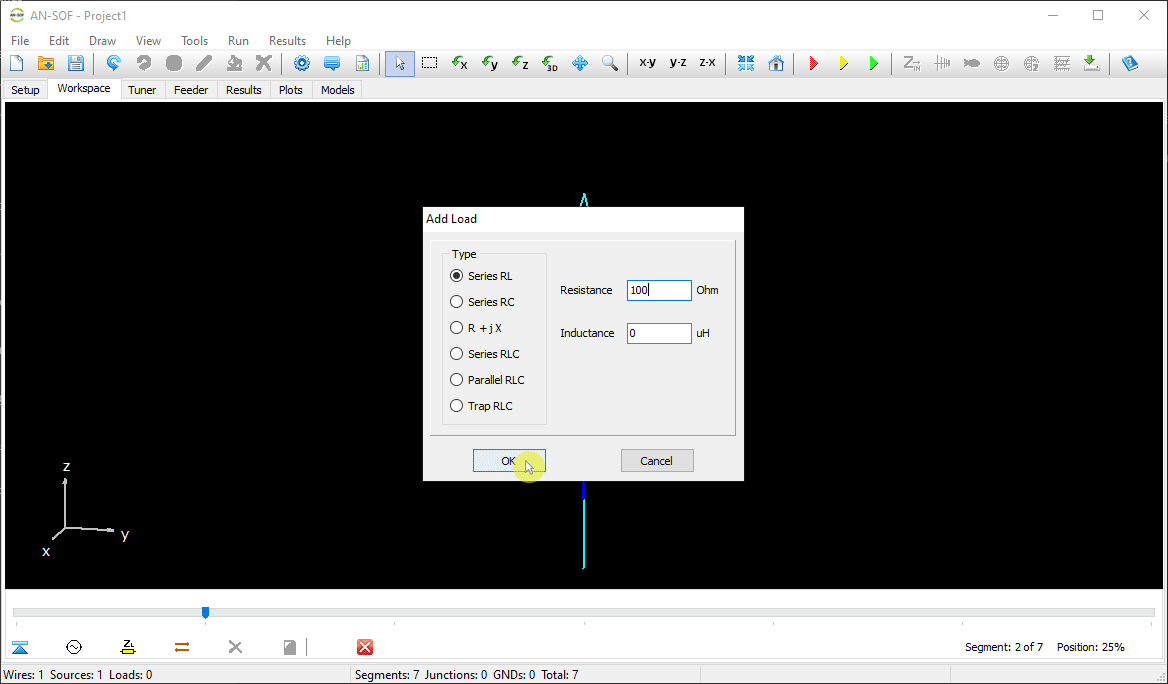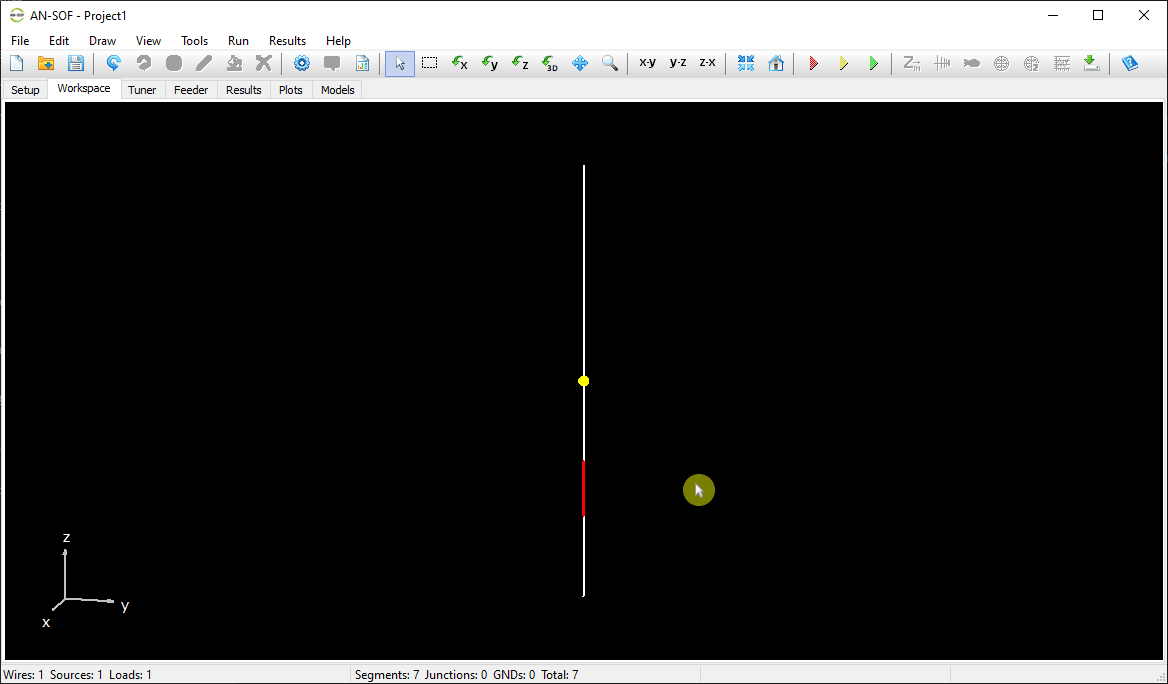
- Load types include (Fig. 2):
- Series RL (resistor + inductor)
- Series RC (resistor + capacitor)
- Fixed R + jX impedance (non-frequency-dependent reactance)
- Series RLC
- Parallel RLC
- Trap (series RL + parallel C)

Tip
- To customize the default color of loads, go to: Main Menu > Tools > Preferences > Workspace tab.
To edit a load on a wire segment, follow these steps:
- Right-click on any part of the wire to open the pop-up menu.
- Select Source / Load / TL (Ctrl +Ins) from the menu to display the Source / Load / TL toolbar.
- Use the slider on the toolbar to select the segment where the load is located.
- Click the Modify button to open the Edit Load dialog box, where you can update the load’s parameters.
- To remove the load, click the Delete button.
- Click the Exit button to close the toolbar.
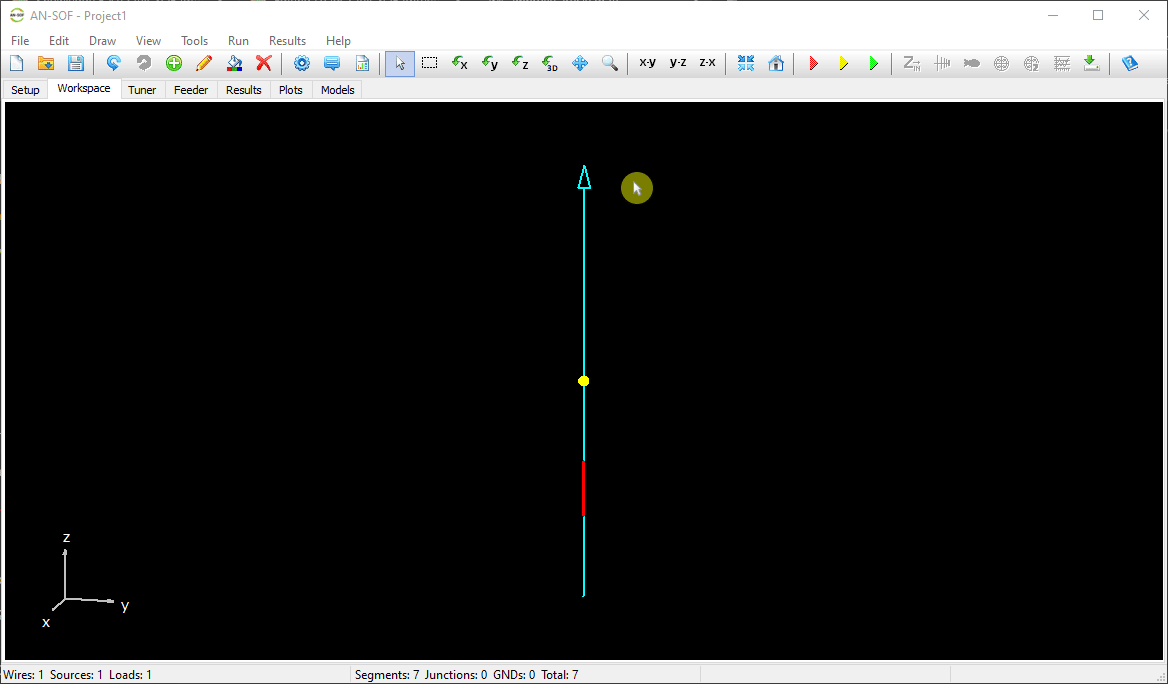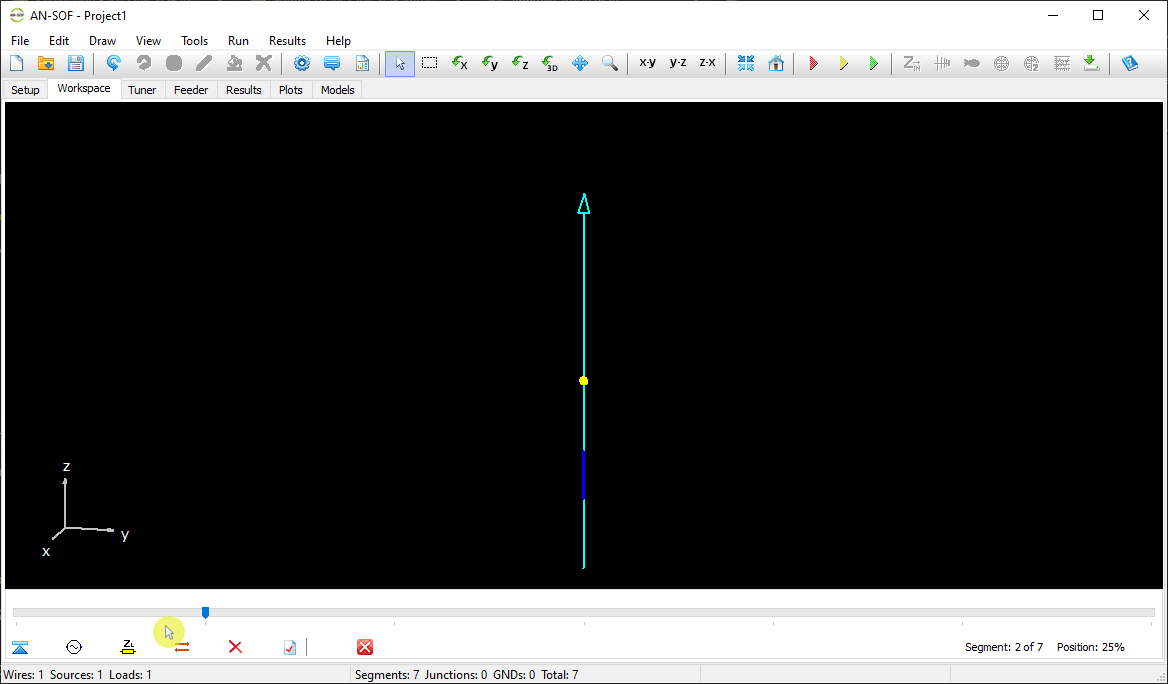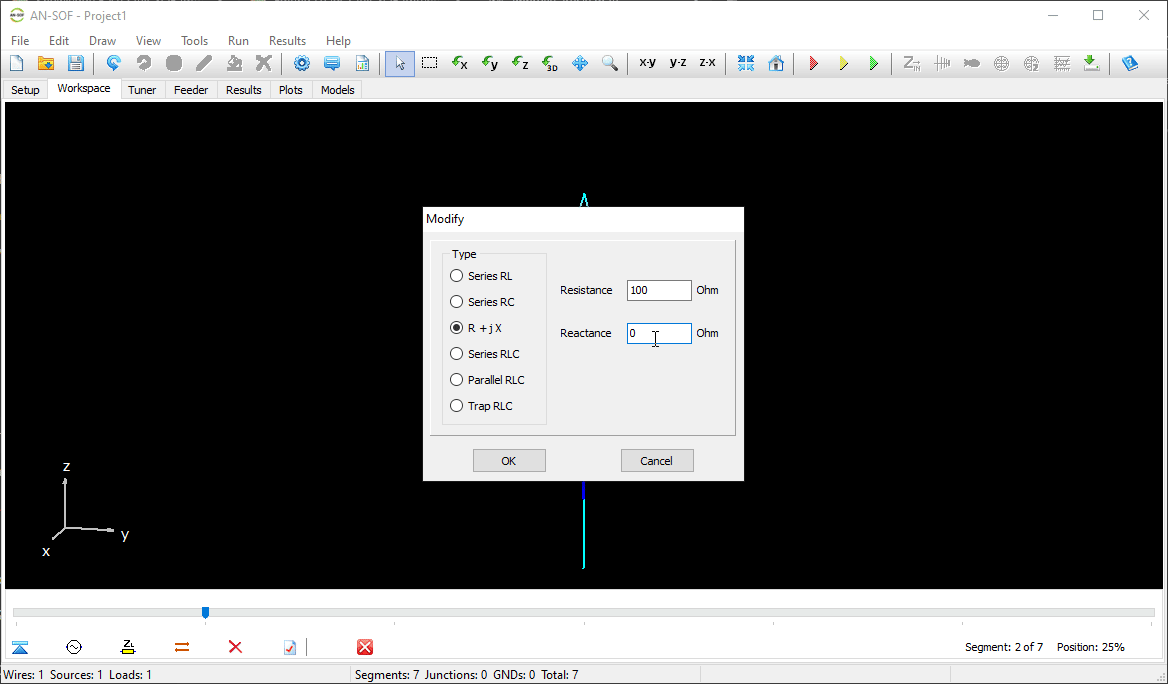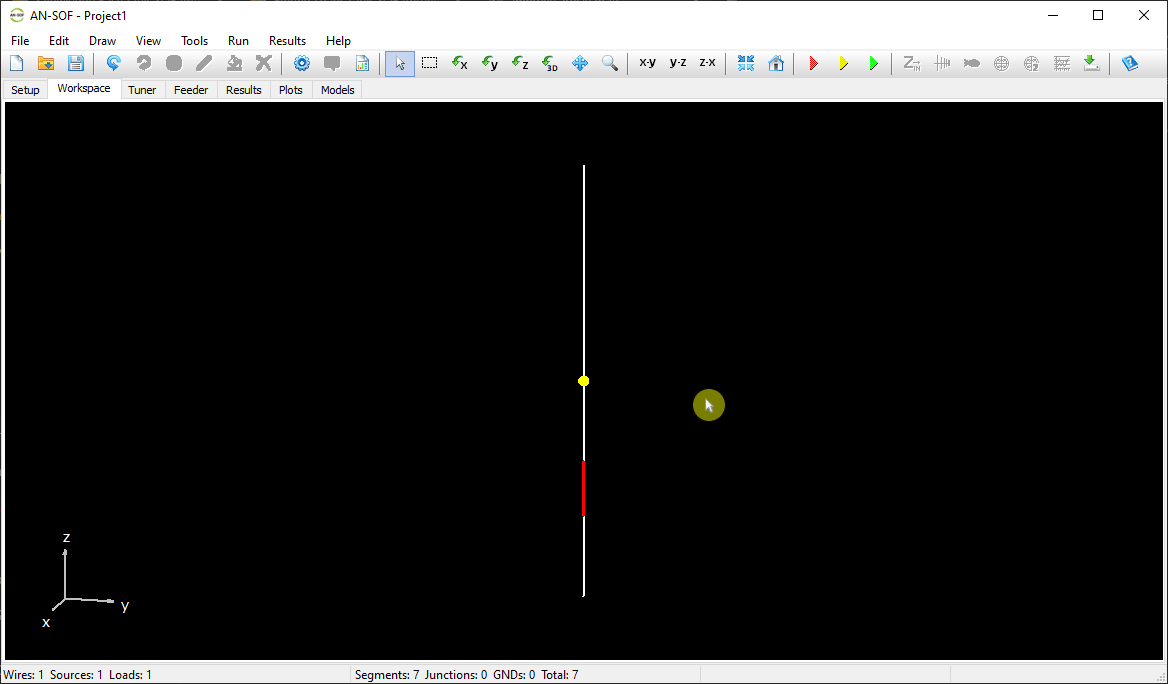
Tip
- To customize the default color of loads, go to: Main Menu > Tools > Preferences > Workspace tab.
You can enable or disable all loads in the simulation without deleting them. This is useful when you want to temporarily exclude load impedances from the analysis.
- Go to the Setup tab and locate the Settings panel in the main window.
- Check or uncheck the Load Impedances option:
- Checked: Loads are enabled and included in the simulation.
- Unchecked: Loads are disabled but remain defined in the model.
See Fig. 1 for reference.
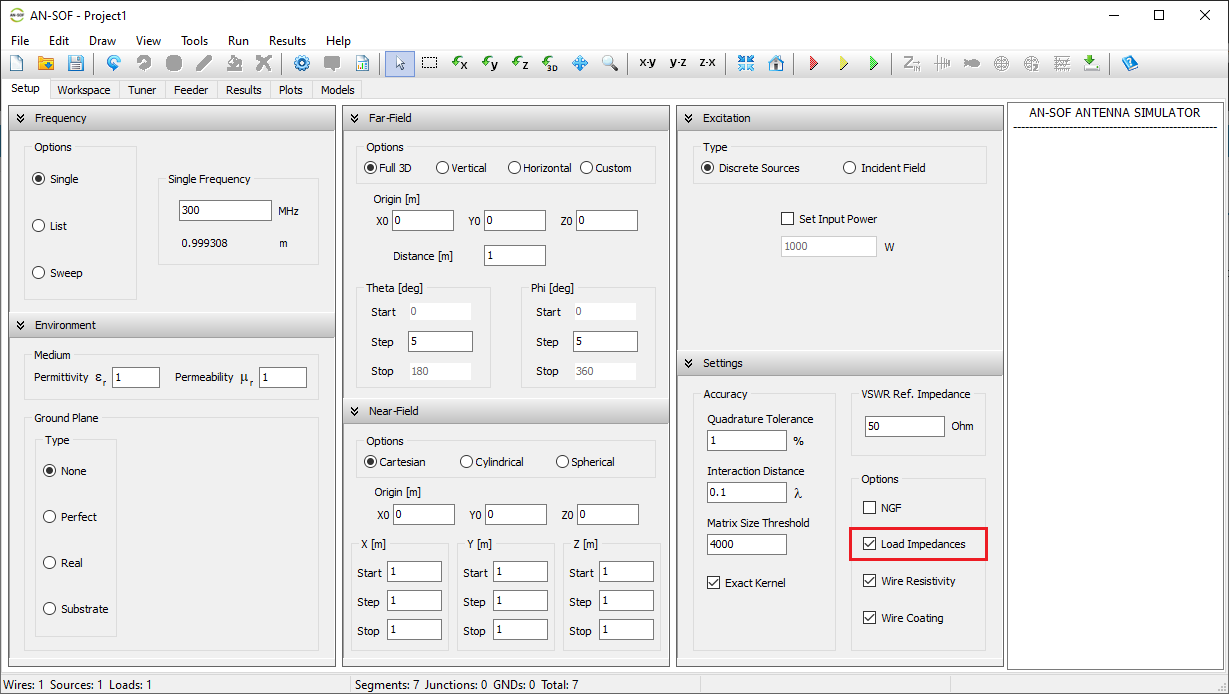
Incident Field
To choose an incident plane wave as excitation of the structure, go to the Setup tab > Excitation panel > and select the Incident Field option, Fig. 1. When this option is selected, if there are discrete sources on the structure, none will be considered in the simulation.
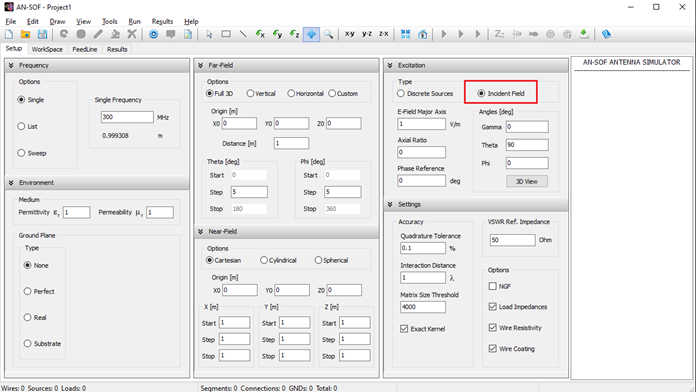
Note
When an incident plane wave is used as the excitation, the calculated far-field and near-field results represent the scattered fields. The resulting radiation pattern is the scattered field pattern, observed in the far-field region where the scattered field amplitude decays with the inverse of the distance (1/r), and the scattered power density decays with the inverse square of the distance (1/r²) from the structure.
The following incident field parameters can be set in the Excitation panel > of the Setup tabsheet after clicking on the Incident Field option:
- E-Field Major Axis: Amplitude, in V/m (Volts rms per meter), of the linearly polarized incoming electric field. For elliptical polarization, it is the length of the major ellipse axis.
- Axial Ratio: For an elliptically polarized plane wave, it is the ratio of the minor axis to the major axis of the ellipse. A positive (negative) axial ratio defines a right-handed (left-handed) ellipse. If the axial ratio is set to zero, a linearly polarized plane wave is defined.
- Phase Reference: Phase, in degrees, of the incident plane wave at the origin of coordinates. It can be used to change the phase reference in the calculation. Its value only shifts all phases in the structure by the given amount.
- Gamma: Polarization angle of the incident electric field in degrees. For a linearly polarized wave, Gamma is measured from the plane of incidence to the direction of the electric field vector, Fig. 1. For an elliptically polarized wave, Gamma is the angle between the plane of incidence and the major ellipse axis.
- Theta: Zenith angle of the incident direction in degrees, Fig. 1.
- Phi: Azimuth angle of the incident direction in degrees, Fig. 1.
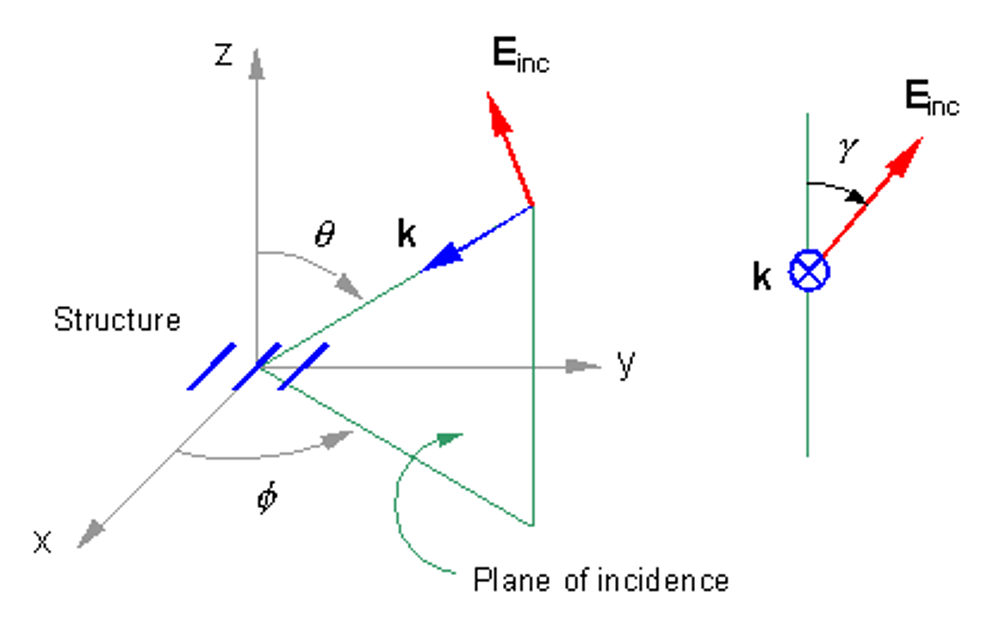
Note
When an incident plane wave is used as excitation, all discrete sources, if any, will not be considered in the simulation.
The 3D-View interface allows us entering the parameters of the incident field in a graphical way. Follow these steps:
- Go to the Setup tabsheet and select the Incident Field option in the Excitation panel >.
- Click on the 3D View button to open the interface and display the Incident Wave dialog box, Fig. 1.
- Set the Gamma, Theta and Phi angles and press ENTER. You can also use the small arrows to change these angles.
- Close the Incident Wave dialog box. The angles that have been entered in the dialog box will appear in the Excitation panel, Fig. 2.
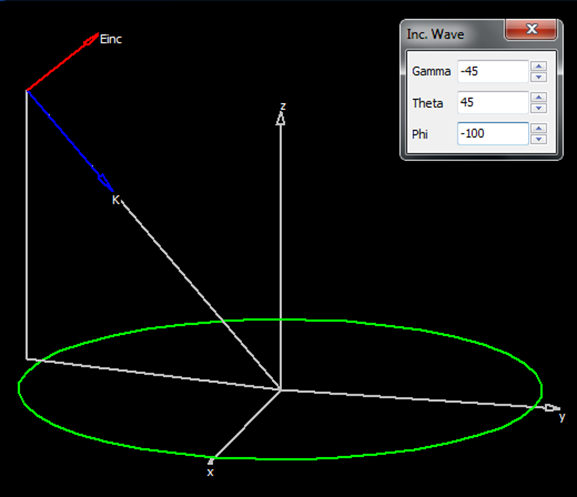
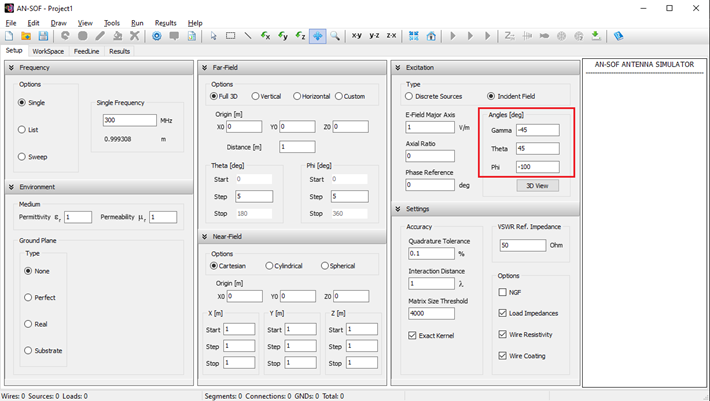
Ground Planes
A perfectly electric conducting (PEC) ground plane, parallel to the xy-plane, can be added to the model using the following procedure:
- Navigate to the Setup tab > Environment panel.
- Select the Perfect option in the Ground Plane box (see Fig. 1).
- Set the ground plane position under the Position label (Z-coordinate).
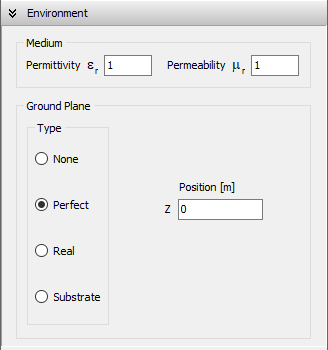
When the Perfect ground is selected, an infinite PEC ground plane will be placed at the specified Z-coordinate relative to the xy-plane:
- If Z > 0, the PEC ground plane will be above the xy-plane.
- If Z = 0, the PEC ground plane will be on the xy-plane.
- If Z < 0, the PEC ground plane will be below the xy-plane.
The ground plane is represented as a square with cross diagonals to visualize its position (see Fig. 2). Note that this is only a symbolic representation, as the ground plane itself is infinite in extent.
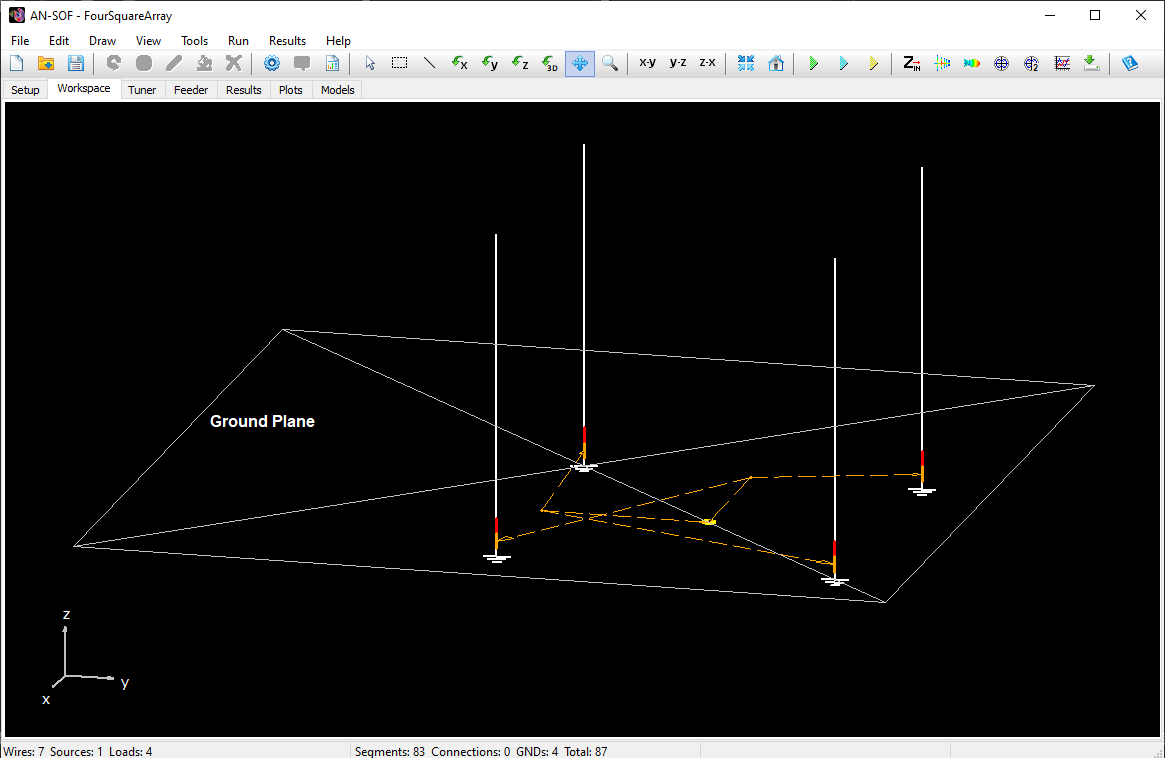
A real (i.e., imperfect or lossy) ground plane, located on the xy-plane (Z = 0), can be added to the model using the following procedure:
- Navigate to the Setup tab > Environment panel.
- Select the Real option in the Ground Plane box (see Fig. 1).
- Specify the Real Ground Option:
- Set the ground Permittivity and Conductivity. If a Radial Wire Ground Screen is selected, also specify the radial length, number of radials, and wire radius.
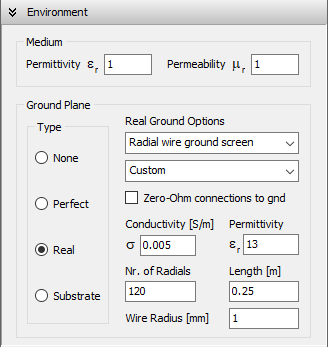
The ground plane is represented as a square with cross diagonals to indicate its position (see Fig. 2). Note that this is only a symbolic representation, as the ground plane itself is infinite in extent. When a Radial Wire Ground Screen is selected, the radial wires lying on the ground will be displayed instead of the ground plane symbol (see Fig. 3).

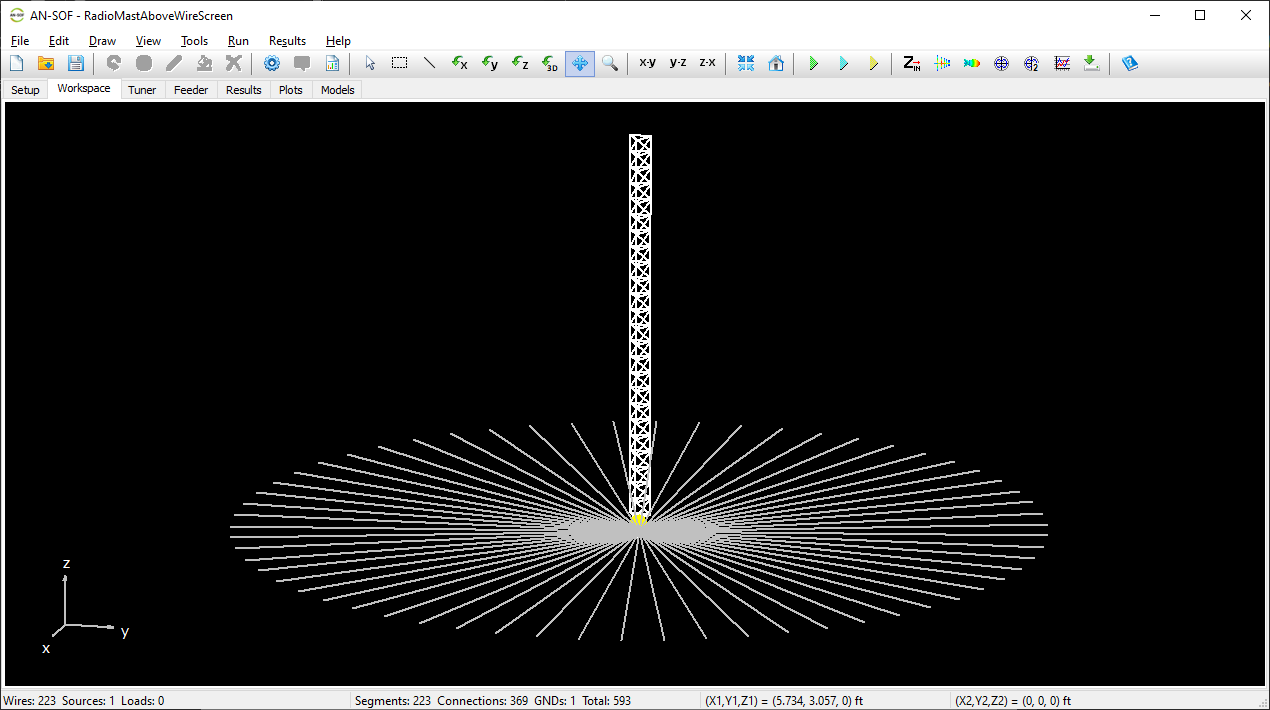
To incorporate a dielectric substrate beneath the xy-plane (Z < 0) into the model, follow these steps:
- Navigate to the Setup tab > Environment panel.
- In the Ground Plane box, select the Substrate option (see Fig. 1).
- Choose between an infinite or finite slab in the Substrate Slab Options box.
- Select a substrate material from the provided list, or choose Custom to specify the substrate’s Permittivity. Set the slab’s Thickness (h) and, if a finite slab is selected, configure its dimensions along the X and Y axes.
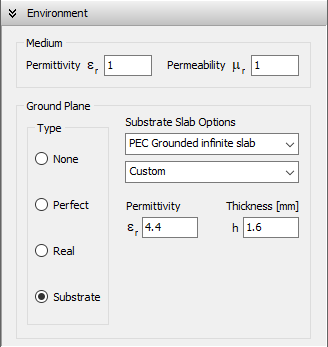
Note:
The substrate slab is backed by a PEC ground plane, which runs parallel to the xy-plane at Z = -h. This ground plane cannot be removed from the simulation (see Fig. 2).

A wire will automatically connect to the ground plane when the z-coordinate of one of its ends coincides with the position of the ground plane.
- When a PEC ground plane is selected, the ground position is specified by the Z value in the Environment panel > Ground Plane box.
- When a real ground is selected, the ground position is Z = 0 (xy-plane).
- When a substrate is selected, a PEC ground plane is placed at Z = -h, where h is the substrate thickness.
Wire connections to the ground plane are indicated with 3D symbols (see Fig. 1).
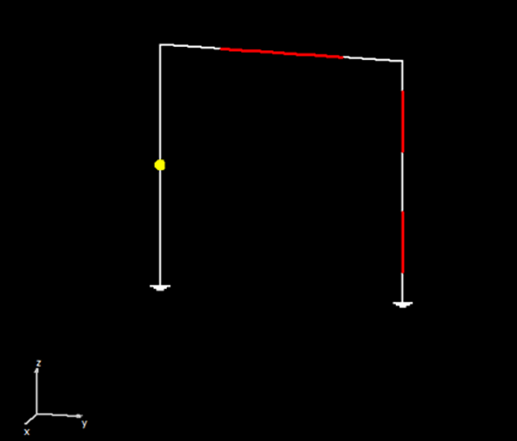
WARNING!
- All wires must be above the ground plane.
- Wires that cross the ground plane from one side to the other are not allowed.
To remove the ground plane, follow these steps:
- Navigate to the Setup tab > Environment panel.
- Select the None (free space) option in the Ground Plane box (see Fig. 1).
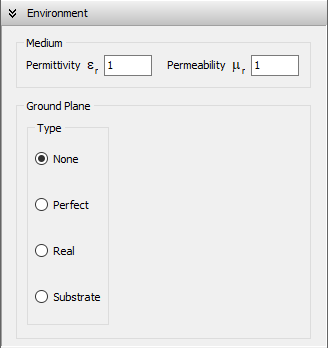
Running Calculations
Once the frequencies, environment, geometry, and excitation are set, AN-SOF is ready to compute the currents flowing on the wire segments.
To calculate the current distribution:
- Navigate to Run > Run Currents (Ctrl + R) in the main menu (see Fig. 1).
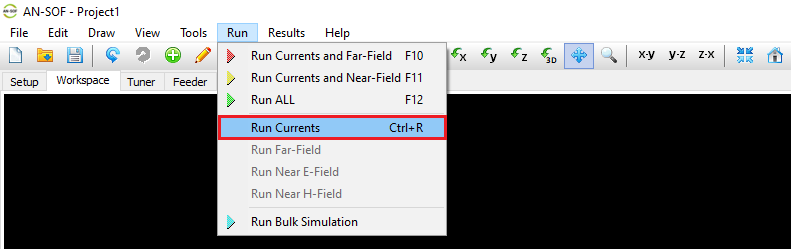
Tip
- When modeling a transmitting antenna and only the input impedance and VSWR/S11 are needed, the Run Currents (Ctrl + R) command saves time by skipping the calculation of the radiated field.
Once the current distribution on the structure has been calculated, the far-field can be computed within the angular ranges specified in the Far-Field panel of the Setup tab.
To calculate the far-field:
- Navigate to Run > Run Far-Field in the main menu (see Fig. 1).
- This command is enabled only after the current distribution has been calculated.
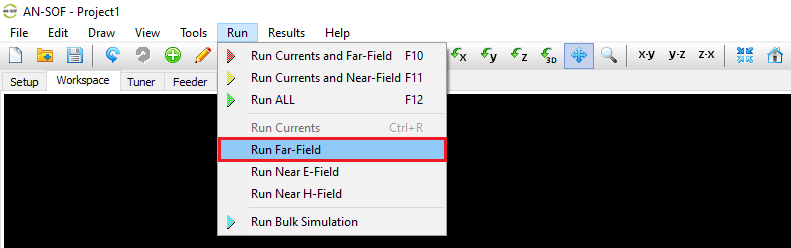
Tip
To sequentially and automatically calculate both the current distribution and the far field, click the Run Currents and Far-Field (F10) button on the toolbar.
Note
When an incident plane wave is used as the excitation, the calculated far-field results represent the scattered field. The resulting radiation pattern is the scattered field pattern, observed in the far-field region where the scattered field amplitude decays with the inverse of the distance (1/r), and the scattered power density decays with the inverse square of the distance (1/r²) from the structure.
Once the current distribution on the structure has been calculated, the near electric field can be computed at the points in space specified in the Near-Field panel of the Setup tab.
To calculate the near electric field:
- Navigate to Run > Run Near E-Field in the main menu (see Fig. 1).
- This command is enabled only after the current distribution has been calculated.
Tips
- To sequentially and automatically calculate both the current distribution and the near fields, click the Run Currents and Near-Field (F11) button on the toolbar. This command also calculates the near H-Field.
- To avoid calculating the H-Field, go to Main Menu > Tools > Preferences > Options and uncheck the “Run ALL” also calculates the H-Field option.
Note
When an incident plane wave is used as the excitation, the calculated near-field results represent the scattered fields.
Once the current distribution on the structure has been calculated, the near magnetic field can be computed at the points in space specified in the Near-Field panel of the Setup tab.
To calculate the near magnetic field:
- Navigate to Run > Run Near H-Field in the main menu (see Fig. 1).
- This command is enabled only after the current distribution has been calculated.
Tips
- To sequentially and automatically calculate both the current distribution and the near fields, click the Run Currents and Near-Field (F11) button on the toolbar. This command also calculates the near E-Field.
- To enable the calculation of the H-Field, go to Tools > Preferences > Options in the main menu and check the “Run ALL” also calculates the H-Field option.
Note
When an incident plane wave is used as the excitation, the calculated near-field results represent the scattered fields.
Once the frequencies, environment, structure geometry, excitation, and far-field observation points have been defined, AN-SOF is ready to perform the calculations. If near-field data is also required, the observation points must first be specified in the Near Field panel. The simulation begins by calculating the current distribution along the wire segments, which also yields the input impedance for a transmitting antenna. The near and far fields are then computed based on these segment currents.
Run ALL (F12) Command
The Run ALL (F12) command allows you to sequentially and automatically calculate the current distribution, far fields, and near fields. To use this command:
- Navigate to Main Menu > Run > Run ALL (F12) (see Fig. 1).
- Alternatively, click the Run ALL button on the toolbar.
Alternative Commands
- If the near field is not required, you can calculate only the currents and far fields by clicking Run > Run Currents and Far-Field (F10). This command is also available on the toolbar.
- If the far field is not required, you can calculate only the currents and near fields by clicking Run > Run Currents and Near-Field (F11). This command is also available on the toolbar.
Separate Calculations
The currents, far fields, and near fields can also be computed separately, as explained in the following articles:
- Calculating the Current Distribution
- Calculating the Far Field
- Calculating the Near E-Field
- Calculating the Near H-Field

When a calculation is executed using the commands under the Run menu, the Processing window will be displayed (see Fig. 1). This window includes a button to abort the calculation at any time.
Note:
You will be prompted to save the project before aborting, as AN-SOF will restart after the process is terminated.
In simulations where the excitation of the structure needs to be changed frequently—such as adjusting the amplitudes of discrete sources or altering the direction of arrival of an incident field—the Numerical Green’s Function (NGF) option can save significant computation time. To enable this option, navigate to the Settings panel of the Setup tab, as shown in Fig. 1.
How NGF Works
- During an NGF calculation, the LU-decomposed matrix of the system is stored in a file after the initial computation.
- Subsequent calculations reuse this stored matrix, allowing them to be performed much faster than the initial one.
Automatic NGF Activation
- When transmission lines are included in the model, the NGF option is automatically enabled.

AN-SOF can import a sequence of input files to generate a corresponding sequence of output files, all without requiring user intervention during the process. The input files must adhere to the NEC format and have a .nec extension. The supported NEC commands for importing wires are described in the section: Importing Wires.
Output Data
The output data includes:
- Power Budget or RCS (Radar Cross Section).
- Input Impedances.
- Far Field and Near Fields.
All output data is provided in CSV format. For each NEC input file, AN-SOF generates an individual project containing .emm and .wre files (see File Formats). This allows each project to be opened separately after the bulk simulation is completed.
Initiating a Bulk Simulation
- Navigate to the main menu and select Run > Run Bulk Simulation.
- A prompt will appear, asking if you want to save changes in the current project, as the bulk simulation requires closing the currently open project.
- A dialog box will be displayed, allowing you to select a directory and the input .nec files.
- After selecting the desired files and clicking the Open button, the bulk simulation will begin. The input files will be imported and computed one after another in alphabetical order.
Generated Files
For an input file named “InputFile.nec”, the following files will be generated:
AN-SOF Project Files
- InputFile.emm: Main project file (can be opened with AN-SOF).
- InputFile.wre: Geometry data (wires, segments, connections).
- InputFile.txt: Comments.
- InputFile.cur: Current distribution.
- InputFile.pwr: Input and radiated powers, directivity, gain, etc.
- InputFile.the: Theta component of the far field.
- InputFile.phi: Phi component of the far field.
- InputFile.nef: Near electric field.
- InputFile.nhf: Near magnetic field.
Output CSV Files with Results
- InputFile_PowerBudget.csv: Input and radiated power, efficiency, gain, etc.
- InputFile_Zin.csv: Input impedances, VSWR, S11, etc.
- InputFile_FarFieldX.csv: E-theta and E-phi far field components.
- InputFile_EFieldX.csv: Near electric field components.
- InputFile_HFieldX.csv: Near magnetic field components.
Note:
- “X” represents the frequency in Hz (e.g., X = 300000000 for a frequency of 300 MHz).
- A FarField, EField, and HField file will be generated for each frequency if a frequency sweep simulation has been configured.
Automating Parameter Variations
Bulk simulations automate the calculation process for multiple NEC files, even if they are unrelated, eliminating the need for manual calculations file by file. They are particularly useful for sequentially running calculations on NEC files generated with varying geometric parameters for an antenna. The results can then be analyzed by reading data from the generated CSV files.
For example, you can create a script to generate a sequence of NEC files for a Yagi-Uda antenna, where the spacing between its elements varies. To learn how to accomplish this and read the output data from the CSV files, refer to the following article: Element Spacing Simulation Script for Yagi-Uda Antennas.
Displaying Results
Commands to Display Results
The output data of a simulation can be listed in tables or displayed in graphs. All results are found under the Results menu, and are categorized into four groups:
Results related to current distribution
- Results > Plot Current Distribution command.
- Results > Plot Currents command.
- Results > List Currents command.
- Results > Export Currents command.
- Results > List Input Impedances command.
Results related to the far field
- Results > Plot Far-Field Pattern command.
- Results > Plot Far-Field Spectrum command.
- Results > List Far-Field Pattern command.
- Results > List Far-Field Spectrum command.
- Results > Power Budget/RCS command.
Results related to the near E-Field
- Results > Plot Near E-Field Pattern command.
- Results > Plot Near E-Field Spectrum command.
- Results > List Near E-Field Pattern command.
- Results > List Near E-Field Spectrum command.
Results related to the near H-Field
- Results > Plot Near H-Field Pattern command.
- Results > Plot Near H-Field Spectrum command.
- Results > List Near H-Field Pattern command.
- Results > List Near H-Field Spectrum command.
Results related to the Power Density
- Results > Plot Power Density Pattern command.
- Results > Plot Power Density Spectrum command.
- Results > List Power Density Pattern command.
- Results > List Power Density Spectrum command.
Tip
See the most relevant results for transmitting antennas in the Results tab of the main window.
Lists and Plots
Listing the currents or input impedances means tabulating them as a function of frequency.
In the case of fields, they can be listed at a given point versus the frequency (Spectrum) or at a given frequency versus the observation point (Pattern).
AN-SOF includes a suite of four tools for plotting results: AN-XY Chart, AN-Smith, AN-Polar and AN-3D Pattern.
The Results tab in the AN-SOF main window (see Fig. 1) displays a table with the primary results for a transmitting antenna, including:
- Input Impedance (Zin = Rin + jXin)
- VSWR
- S11
- Directivity
- Gain
- Radiation Efficiency
- Horizontal (H) and Vertical (V) Front-to-Rear (F/R) and Front-to-Back (F/B) Ratios
This table is automatically populated only when the wire structure is excited by a discrete source. It will not be filled if the excitation is an incident wave. The tabulated results persist until a new calculation is performed, allowing you to reference them at any time, even when making changes to the project. To export these results to a CSV file, click the Export Results button on the toolbar (see Fig. 1).
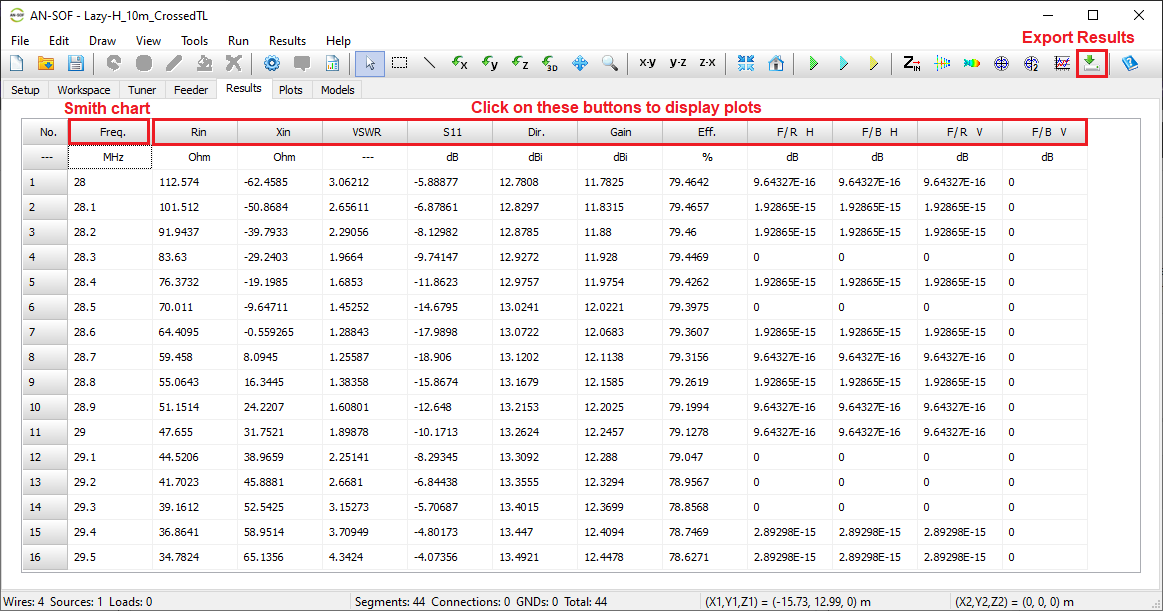
Interactive Column Headers
The column headings, from Rin through F/B V, are interactive buttons. Clicking on them displays rectangular plots, where the data in the column is plotted as a function of frequency.
- Click the “Freq.” column header to display the input impedance (Zin = Rin + jXin) in a Smith Chart. By default, this is the input impedance at the antenna feedpoint.
- If the antenna has a feeder and/or tuner connected to its terminals, the impedance seen at the feeder input or tuner input can also be tabulated in the Results tab. These can be plotted against frequency in rectangular or Smith charts by clicking the corresponding column headers.
Plotting Impedance at Different Points
- Navigate to the Plots tab > “Zin” box (see Fig. 2) and choose between Antenna, Feeder, or Tuner.
- Go to the Results tab, where Rin, Xin, VSWR, and S11 will be tabulated for the selected option (antenna, feeder, or tuner input).
- Click the header buttons as indicated in Fig. 1 to plot these results against frequency.
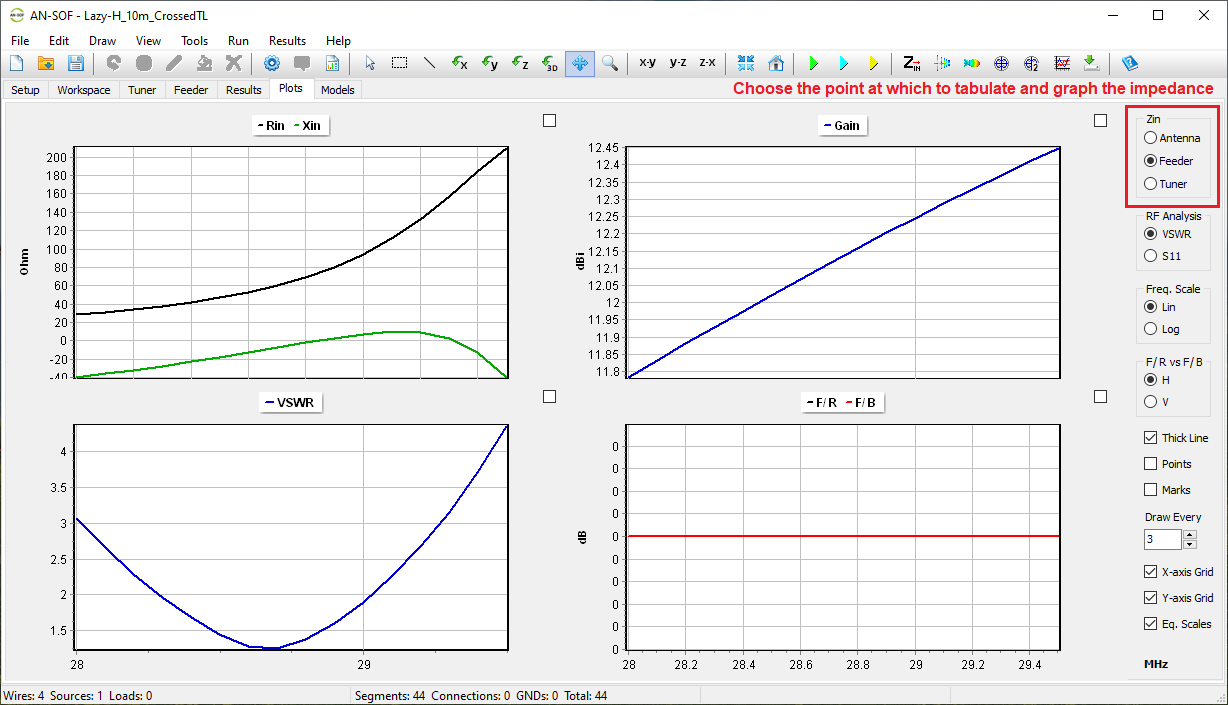
Select the Plots tab in the AN-SOF main window to visualize the plots of the main results for a transmitting antenna as a function of frequency, as shown in Fig. 1. These results are derived from the table in the Results tab.
Plot Layout
- Left Column: Displays the real and imaginary parts of the input impedance (Zin = Rin + jXin) and the VSWR.
- Right Column: Shows the antenna gain in dBi and the Front-to-Rear (F/R) and Front-to-Back (F/B) ratios in dB.
The plots are aligned vertically to facilitate easy comparison.
Customizing Plots
Use the controls on the right side of the Plots tab to adjust various aspects of the graphics, including:
- Line thickness.
- Visualization of points and marks.
- Scales and axes.
- Selection between VSWR or S11.
- Choice between Horizontal (H) or Vertical (V) F/R and F/B ratios.
Each plot can be maximized by clicking the Maximize checkbox located in its upper-right corner.
Input Impedance and VSWR/S11 Options
The input impedance and VSWR/S11 plots can represent:
- The antenna input impedance.
- The feeder + antenna input impedance.
- The tuner input impedance.
The tuner and feeder can be configured in their corresponding tabs next to the Results tab. Whenever a tuner or feeder parameter is changed, the recalculated results in the Results and Plots tabs can be refreshed by selecting the desired option under the Zin box (highlighted in Fig. 1).
Tuner Option
If the Tuner option is selected:
- The input impedance of the tuner will be displayed.
- If the tuner is connected to a combination of feeder + antenna, the input impedance and VSWR/S11 of the tuner + feeder + antenna system will be displayed.
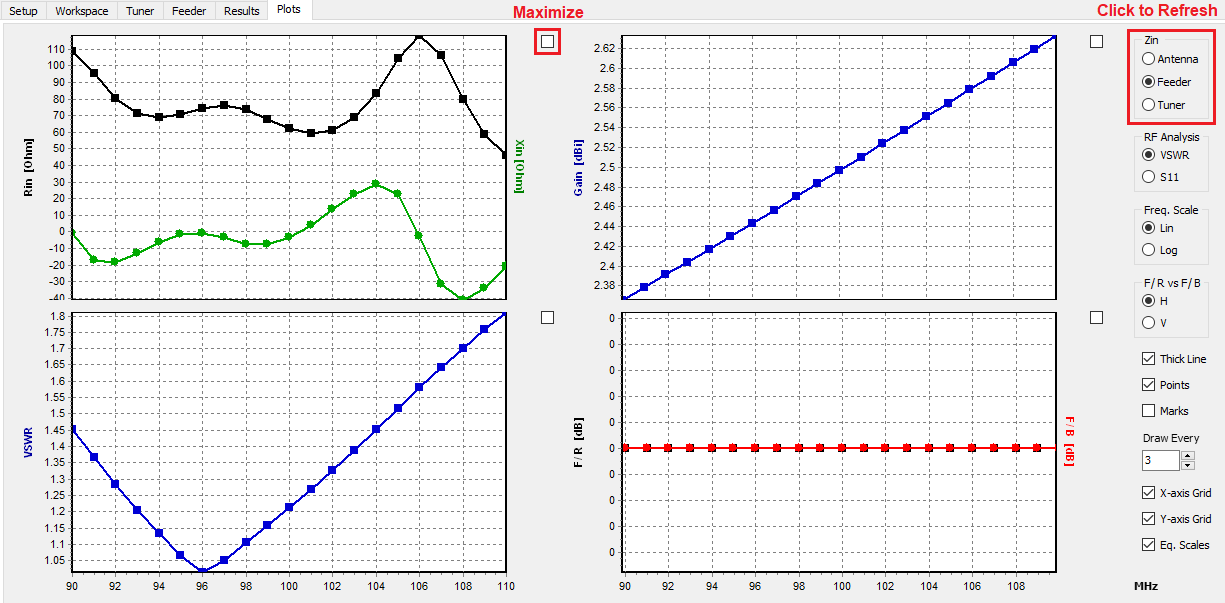
Current Distribution
Go to Results > Plot Current Distribution in the main menu to display a 3D graph of the current distribution on the structure. This command executes the AN-3D Pattern > application where the amplitude of the currents is displayed on the structure using a color scale. Additionally, the currents in phase, real, and imaginary parts can be plotted selecting these options in the Plot menu of AN-3D Pattern, Fig. 1.

A 2D plot of the current distribution along a selected wire can be shown by right clicking on the wire and choosing Plot Currents from the pop-up menu, Fig. 2. The Plot Currents command executes the AN-XY Chart > application, where the current is plotted in amplitude vs. position along the selected wire. The current distribution can also be plotted in phase, real and imaginary parts by choosing these commands under View in the AN-XY Chart main menu.
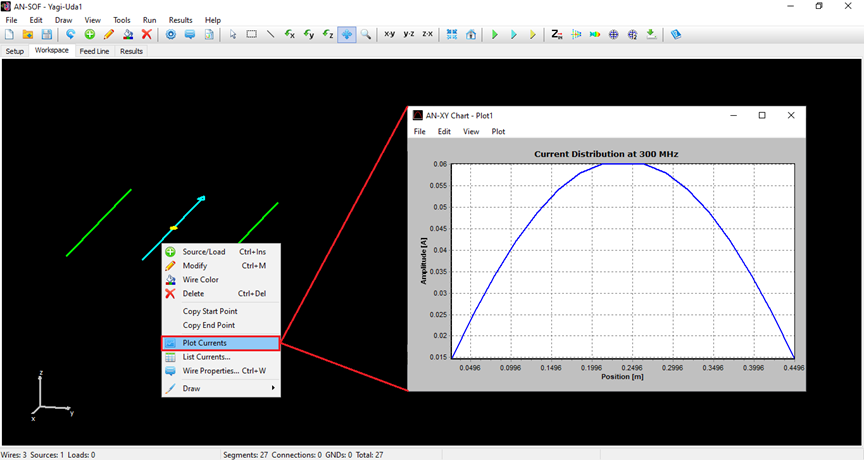
A wire can also be selected by first clicking on the Select Wire button (arrow icon) on the toolbar and then left clicking on the wire. Once the wire is selected, go to Results > Plot Currents in the main menu to plot the current along that wire. This command is enabled when the current distribution has been calculated.
Tips
- The graph plotted by AN-XY Chart can be zoomed by expanding a box with the left mouse button pressed on the plot.
- Right click on the graph and drag the mouse to move it.
- Left click and expand a rectangle up to return to the original view.
- There are options to change the units of the plotted magnitudes and to export data in the AN-XY Chart main menu.
Right clicking on a wire shows a pop-up menu >. Click on the List Currents command to display the List Currents toolbar, Fig. 1. This toolbar allows us to select a wire segment to see the current flowing through that segment versus frequency. If the segment has a source or load, the list of input impedances, admittances, voltages, powers, reflection coefficient, VSWR, return and transmission losses can also be displayed.
A wire can also be selected by first clicking on the Select Wire button (arrow icon) on the toolbar and then left clicking on the wire. Once the wire is selected, go to Results > List Currents in the main menu. This command is enabled when the current distribution has been calculated.
The List Currents toolbar has the following components:

The Slider
Each position of the slider corresponds to the position of a segment along the selected wire. Thus, the slider allows us selecting the desired wire segment. The position of the selected segment is shown at the right corner of this toolbar. The segment position is shown as a number and as a percentage of the wire length. The percentage position is measured from the starting point of the wire to the middle point of the segment, namely,
% position = 100 (position / wire length)
The 50% button
Moves the slider towards the center of the wire. Note that there must be an odd number of segments for there to be a segment at the midpoint of the wire.
The Current on Segment button
Displays the Current on Segment dialog box, Fig. 2, showing a list of the current in the selected segment versus frequency. Click the Plot button to plot the current in the segment as a function of frequency.

The Input List button
If the selected segment has a source on it, the Input List button will be enabled. Click this button to display the Input List dialog box, Fig. 3, where the list of input impedances, admittances, currents, voltages, and powers is shown. Select an item from the list in the upper right corner of the window and then press the Plot button to plot the selected item versus frequency. The input impedance can be plotted in a Smith chart by pressing the Smith button. Click the Export button to save the list in CSV format.
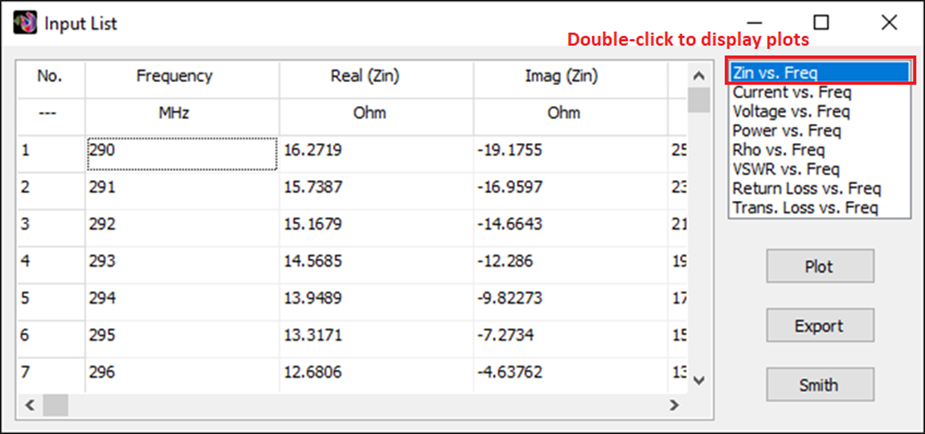
The Source List button
If the selected segment has a source on it, the Source List button will be enabled. Click this button to display the Source List dialog box, Fig. 4, where the list of currents, voltages, and powers in the source internal impedance is shown. Select an item from the list in the upper right corner of the window and then press the Plot button to plot the selected item versus frequency. Click the Export button to save the list in CSV format.
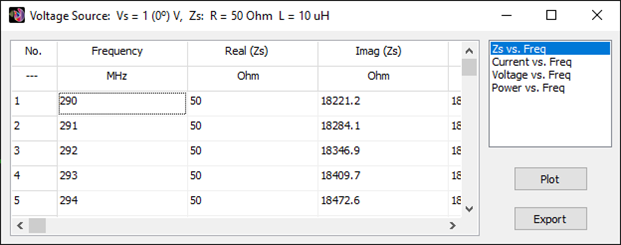
The Load List button
If the selected segment has a load on it, the Load List button will be enabled. Click this button to display the Load List dialog box, Fig. 5, where the list of load impedances, currents, voltages, and powers in the segment is shown. Select an item from the list in the upper right corner of the window and then press the Plot button to plot the selected item versus frequency. Click the Export button to save the list in CSV format.
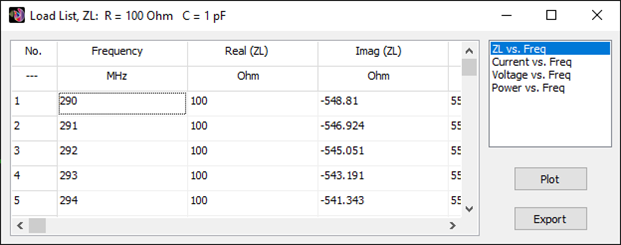
The Exit button
Closes the List Currents toolbar.
The following procedure allows us to select a wire segment to tabulate currents versus frequency:
- Right click on the wire to display the pop-up menu >.
- Click on the List Currents command to display the List Currents toolbar >.
- Move the slider and select the desired segment on the wire.
- Click on the Current on Segment button to display the Current on Segment dialog box, where a list of the currents versus frequency is shown. Currents are shown in amplitude, phase, real and imaginary parts. Click the Plot button to plot the current in the selected segment as a function of frequency.
The currents flowing on a wire can be exported to a CSV (Comma-Separated Values) file. Since the current is calculated at the midpoint of each wire segment, the current distribution is sampled at a finite set of points determined by the number of segments the wire is divided into. Additionally, as the current varies with frequency, there is a unique current distribution along the wire for each frequency.
To export the current distribution as a function of position along a selected wire and as a function of frequency, follow these steps:
- Click the Select Wire button (arrow icon) in the toolbar.
- Left-click on the wire to select it (it will be highlighted in light blue).
- Navigate to the Results menu > Export Currents in the main menu (see Fig. 1).
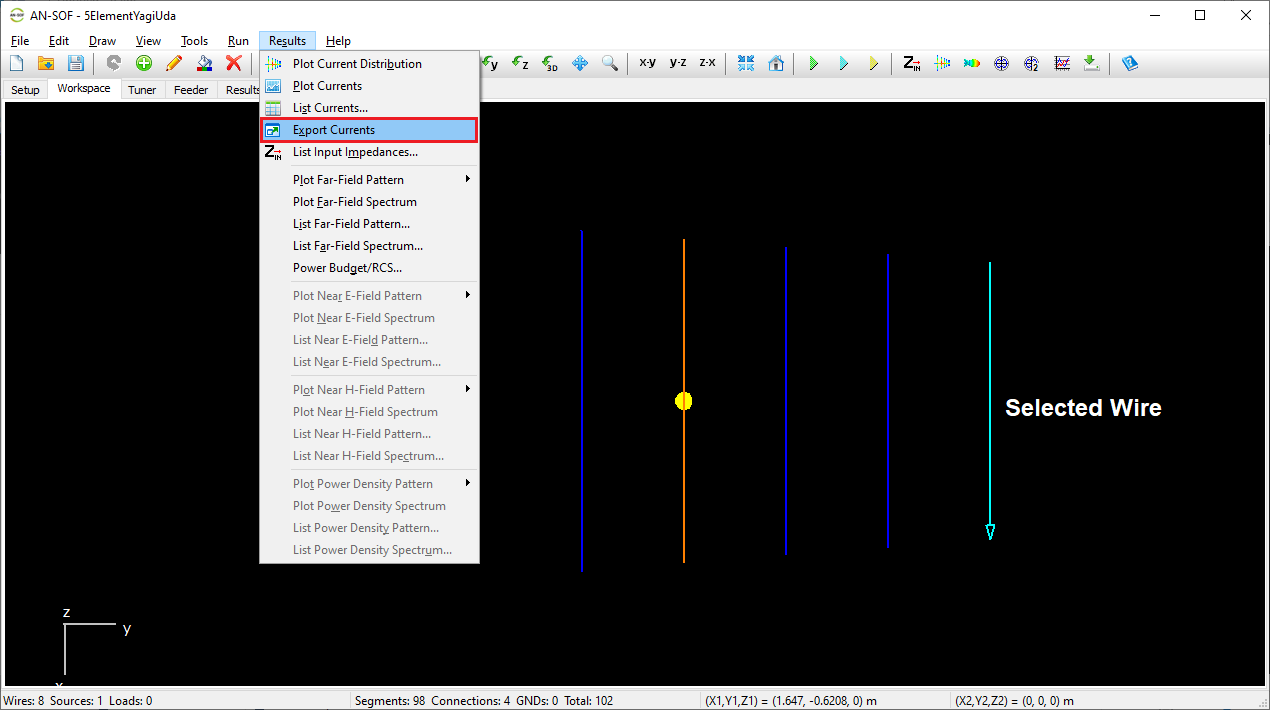
The complex current (real and imaginary parts) is tabulated based on the position along the wire. Position and frequency units can be configured in the Preferences window.
Note:
- Position is measured from the start point of the selected wire (the end without the arrow when selected).
- The exported CSV file contains the real and imaginary parts of the current as a function of position and frequency, as shown in Fig. 2.
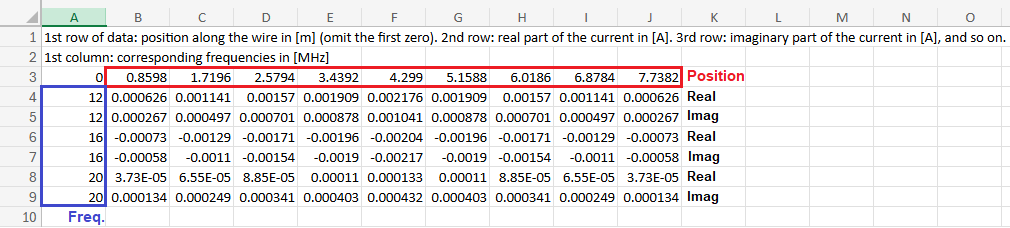
Input Impedances
The following procedure allows us to select a segment that has a source to tabulate input impedance versus frequency:
- Right click on a wire that has a source to display the pop-up menu.
- Click on the List Currents command to display the List Currents toolbar.
- Move the slider and select the segment where the source is placed.
- Click on the Input List button to display the Input List dialog box, where the list of input impedances, admittances, currents, voltages, powers, reflection coefficient, VSWR, S11 in decibels, return and transmission losses is shown. Select an item from the list in the upper right corner of the window and then press the Plot button to plot the selected item versus frequency. Click the Smith button to plot the input impedance in a Smith chart.
Tips
- The reference impedance for reflection calculations (VSWR, S11, and Return Loss) can be set in the Settings panel of the Setup tabsheet.
- When there is a single source on the structure, you can quickly access the input impedance by going to the main menu > Results > List Input Impedances or by clicking on the ‘List Input Impedances’ button on the toolbar.
The Tuner Calculator
AN-SOF features a tuner calculator that enables impedance matching of an antenna input impedance, an antenna with a feeder already connected to its terminals, or a given custom load.
To access the tuner calculator, choose the Tuner tab in the AN-SOF main window (Fig. 1). Here, you can set the tuner parameters on the left side of the window and view the results on the right side. The tuner consists of three components, each of which will be described in the following sections:
- Impedance Matching Network: This component allows the synthesis of an impedance matching network based on the impedance seen at the network output and the desired impedance at the network input. The quality factors of the network, inductors, and capacitors can be adjusted to model real-world scenarios.
- Stray Capacitance: Some networks, particularly high-pass Tee networks, exhibit a parallel stray capacitance at the network output. This capacitance can be specified to account for this effect.
- Impedance Transformer: An impedance transformer can be specified at the network output to transform the input impedance of an antenna, the input impedance of a feeder connected to an antenna, or a custom load entered by the user. It can represent devices such as baluns and ununs — for example, a 1:1 balun for balanced-to-unbalanced conversion without impedance change, a 1:4 balun to match a 200-ohm antenna to a 50-ohm feedline, or a 1:9 unun for matching high-impedance long-wire antennas. This feature is useful for optimizing power transfer and minimizing VSWR in multiband and off-resonance antenna configurations.
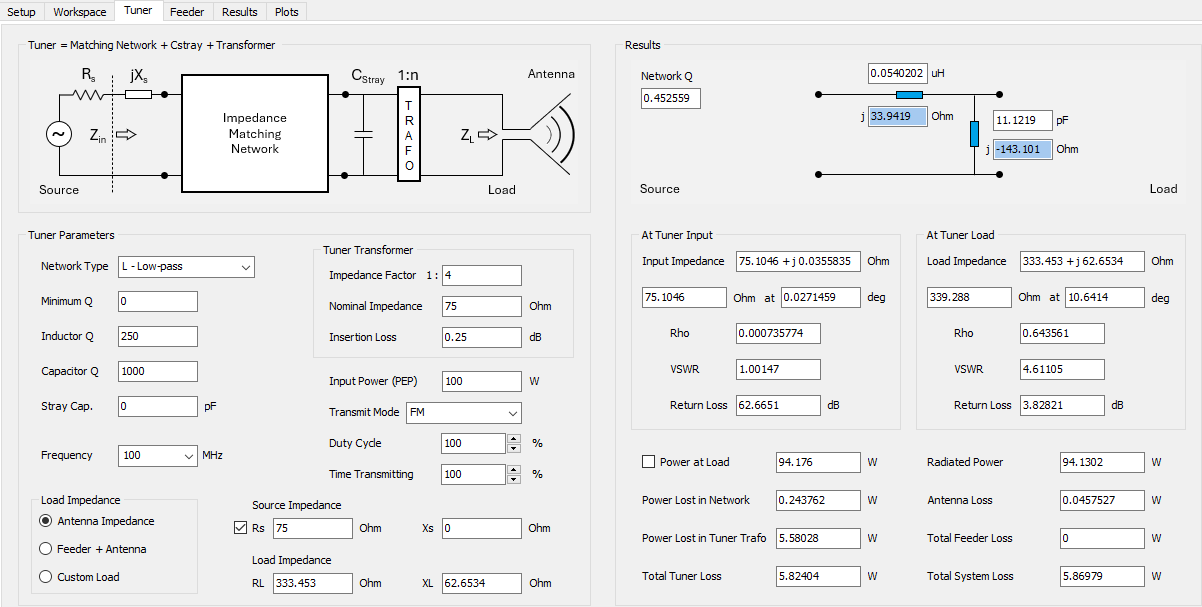
Impedance Matching Network
In the Tuner Parameters box, you can configure the impedance matching network, as shown in Fig. 2.
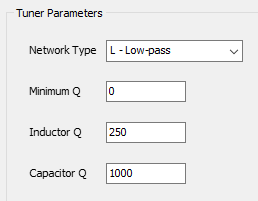
By expanding the Network Type dropdown menu, you have the following options:
- No Network: Select this option to bypass the matching network, making the network input impedance equal to the impedance at the network output.
- Based on the impedance seen at the network output and the source impedance connected to the network input side, AN-SOF can synthesize the following networks:
- L – Low-pass
- L – High-pass
- PI – Low-pass
- PI – High-pass
- T – Low-pass
- T – High-pass
The network components will be automatically calculated to match the source impedance (Rs + jXs) connected to the network input side. If the source impedance has a reactance component, jXs, the network will “absorb” this reactance so that the input impedance of the network plus jXs will match the real part, Rs, of the source impedance. The same principle applies to the load impedance seen at the network output side. If the network load impedance has an imaginary part, it will be absorbed by the network to synthesize the network components (inductors and capacitors).
Note that a low-pass network could include series capacitors instead of inductors or parallel inductors instead of capacitors, depending on the complex impedances (with real and imaginary parts) being matched. Similarly, a high-pass network might involve series inductors instead of capacitors or parallel capacitors instead of inductors.
You can specify a minimum Q for the network synthesis calculations, as well as the Q for the inductors and capacitors. This allows you to account for component losses to represent real-world components. To model ideal zero-loss components, enter high Q values, such as 1E8.
Stray Capacitance
Stray capacitance, also known as parasitic capacitance, refers to unintended capacitance between two conductors separated by a dielectric or free space. This effect is particularly noticeable at the network output side when a transmission line is connected. AN-SOF allows for the configuration of a feeder composed of a transmission line to feed an antenna, enabling modeling of stray capacitance to accommodate this scenario. While stray capacitance is commonly observed in Tee high-pass networks, it can be added in any case. Typical values range from around 10 pF in HF bands.
Impedance Transformer
In the Tuner Parameters box, an impedance transformer, also known as a “trafo” in RF jargon, can be specified, as shown in Fig. 3.
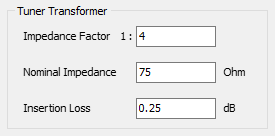
The transformer allows us to divide a load impedance by a factor, n, making it a 1:n transformer. It’s important to note that this is the impedance transformation factor, not the voltage transformation factor, which is n-1/2 and is determined by the primary-to-secondary winding relationship of a transformer. A transformer can be used to reduce a high impedance to approach the standard 50 or 75 Ohms used in transmission lines and RF devices. Both the real and imaginary parts of the load impedance will be divided by n.
If n is in the range 0 < n < 1, the transformed impedance will be higher than the load impedance connected to the output side of the transformer. A factor n = 1 can be used to model a 1:1 transformer, also known as an isolation transformer, which is used to transfer voltage from one electrical circuit to another and to isolate a powered device from the power source. The 1:1 ratio transformer has the same input and output voltage and current. It is used to protect secondary circuits and individuals from electrical shocks between energized conductors and earth ground. It also reduces voltage spikes in the power supply line caused by rapid changes in lighting, static electricity, or voltage.
Real-life transformers are manufactured for a specified nominal impedance transformation. The nominal impedance can be entered in the Tuner Transformer box, as well as the transformer insertion loss in decibels. Manufacturers specify a transformer insertion loss relative to a nominal impedance, so it is important to specify the nominal impedance as well. The insertion loss is defined as the power lost inside the transformer, measured in dB relative to the input power. Thus, the output power delivered by the transformer to the load impedance will be lower than the input power due to losses inside the transformer materials (coil conductor losses, magnetic core losses, etc.).
Tuner Frequency and Input Power
The components synthesized in the impedance matching network of the tuner will be automatically calculated for a specified frequency, which can be chosen from a dropdown menu in the Tuner Parameters box, as shown in Fig. 4.
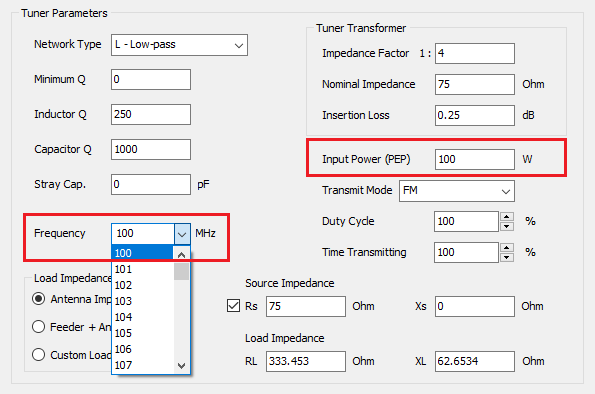
This list of frequencies is taken from the Frequency panel in the Setup tab, where a single frequency, a list of frequencies, or a frequency sweep can be configured. Therefore, to change the list of frequencies available in the Tuner tab, go to the Setup tab and enter the desired frequencies in the Frequency panel. Note that the frequency chosen for the tuner will be its design frequency; thus, the tuner components, inductors, and capacitors will be recalculated if the design frequency changes.
The Input Power to the tuner can also be specified in the Tuner Parameters box. This is the power delivered by the source connected to the input side of the impedance matching network of the tuner. This input power affects the powers calculated in the Results box on the right side of the Tuner tab, as explained below. It is worth mentioning that the tuner input power is not the power delivered to the antenna terminals, which can be set in the Excitation panel of the Setup tab. However, if the tuner is connected to an antenna, we can specify that the tuner output power be delivered to the antenna terminals, as detailed below.
Transmit Mode, Duty Cycle, and Time Transmitting
The input power specified is the transmitter’s Peak Envelope Power (PEP). However, when performing RF exposure evaluations, the average power supplied by the transmitter over time is the critical factor. The average power is a fraction of the PEP, determined by the duty cycle (or duty factor) of the selected transmit mode. The transmit mode can be chosen, and the corresponding percentage duty cycle will be displayed, as shown in Fig. 5. To enter a custom duty cycle, select “Custom” as the transmit mode.
It is also important to account for the percentage of time the transmitter remains active within a specific period, such as 6 minutes. For example, if the telegraph mode transmits for only 3 minutes in every 6-minute period, the power considered for RF exposure calculations is reduced by 50%. Therefore, the Time Transmitting parameter can be set as a percentage. Both the duty cycle and the time transmitting percentage will affect the PEP, and an average input power will be calculated accordingly.
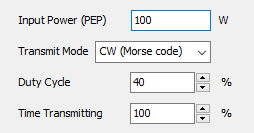
Tuner Source and Load Impedances
The source impedance connected to the tuner input side can be set in real (Rs) and imaginary (Xs) parts, as shown in Fig. 6.
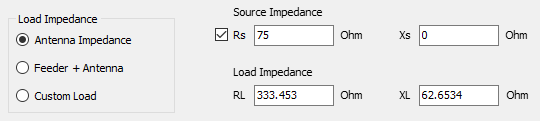
When a non-null source reactance, Xs, is entered, it will be absorbed by the impedance matching network calculations. Thus, the net input impedance of the network, after adding jXs, will be matched to the real part of the source impedance, Rs. Click on the checkbox next to the “Rs” label to set this resistance as the reference impedance for VSWR calculations. This same resistance will be automatically set in the Settings panel as the “VSWR Ref. Impedance”.
There are three options for the tuner load impedance (RL + jXL):
- Antenna Impedance: Select this option to set the antenna input impedance as the tuner load. Note that the antenna impedance varies with frequency, so changing the design frequency for the tuner will trigger a recalculation of the impedance matching network.
- Feeder + Antenna: This option allows us to set the combination of feeder + antenna as the tuner load. In this case, the feeder parameters will be taken from the Feeder tab at the chosen design frequency. Therefore, the load impedance connected at the tuner output is a function of frequency since it is the input impedance to the feeder connected to the antenna.
- Custom Load: This option allows setting a tuner load impedance manually by specifying its real (RL) and imaginary (XL) parts. The Tuner tab can be used as an independent impedance matching calculator in this case.
Tuner Results
The results of the calculations based on the configured tuner parameters are displayed in the Results box on the right side of the Tuner tab, as shown in Fig. 7.

The results are categorized into three sections: Network results, input and load impedances, and power results.
Network Results
The network results shown include the resulting network Q and a diagram illustrating the network components, including inductors and capacitors. For inductors, their inductance in Henry and reactance in Ohms will be displayed, while for capacitors, their capacitance in Farads and reactance in Ohms will be shown. The units of inductance and capacitance displayed can be changed to pH, nH, uH, mH, H, or pF, nF, uF, mF, F, respectively, by navigating to the AN-SOF main menu > Tools > Preferences > Units tab.
It’s worth mentioning that the resulting network Q for L-type networks is determined only by the impedances connected to the load and source side of the network. Therefore, the minimum Q specified in the Tuner Parameters box has no effect for L networks.
Tuner Input and Load Impedances
The resulting input impedance to the tuner will be displayed in both real and imaginary parts, along with a polar representation showing its magnitude in Ohms and phase in degrees. If the source impedance, Rs + jXs, connected to the tuner has a non-null reactance, jXs, this will be absorbed by the impedance matching network. Consequently, the displayed tuner input impedance represents the impedance seen towards the tuner just after Rs, as illustrated in the diagram on the left side of the Tuner tab (Fig. 8).
The load impedance connected to the tuner output terminals will also be shown, which can be the antenna input impedance, a feeder + antenna combination, or a user-entered impedance in the Tuner Parameters box on the left side of the Tuner tab.
For both the tuner input and load impedances, the reflection coefficient (Rho), VSWR, and return loss in dB will be displayed. These values are referred to the reference impedance for VSWR, which has been configured in the Settings panel of the Setup tab.
Powers Delivered and Lost
At the bottom of the Results box, the following powers are calculated:
- Power at Load: This is the power effectively delivered to the tuner load impedance. Note that the tuner consists of the impedance matching network + stray capacitance + transformer sequence. Therefore, the power at the tuner load represents the power delivered at the transformer output terminals. If an antenna impedance is chosen as the tuner load, the “Power at Load” is the power delivered to the antenna terminals. If a feeder + antenna is chosen as the tuner load, the “Power at Load” is the power delivered to the feeder terminals. To apply this power to the antenna model in the Workspace tab, check the checkbox next to the “Power at Load” label.
- Power Lost in Network: This is the total power lost in the network components, including inductors and capacitors, due to the losses related to the specified quality factors, Q. In the impedance matching network, a resistance, R = X/Q, representing component losses, is added in series to the inductor and capacitor reactance, X.
- Power Lost in Tuner Trafo: This is the power lost in the impedance transformer due to the specified insertion loss.
- Total Tuner Loss: This is the sum of the network and transformer losses.
- Radiated Power: If an antenna impedance is set as the tuner load, this is the power effectively radiated by the antenna after discounting losses in the antenna system. If a feeder + antenna is set as the tuner load, this is the power radiated by the antenna after discounting losses in the feeder and the antenna system.
- Antenna Loss: This is the power lost in the antenna structure, considering conductor losses, transmission line losses, if any, and ground plane losses.
- Total Feeder Loss: If a feeder + antenna is chosen as the tuner load, this is the power lost in the feeder system.
- Total System Loss: This is the sum of the power lost in the tuner (network + transformer), antenna (conductors, transmission lines, and ground plane), and feeder (feeding line + transformer), if specified.
The input impedance as a function of frequency can be plotted in a Smith chart by clicking the Smith button in the Input List > dialog box. Follow the procedure described in Listing the Input Impedances > for listing the input impedances versus frequency, and then click the Smith button in the opened dialog box.
Left click on the impedance curve in the Smith chart to see the frequency, input impedance (Zin), reflection coefficient (Rho) and VSWR in a hint message, Fig 1. Go to the AN-Smith main menu > Plot > Admittance to plot the input admittance curve. Go to Edit > Preferences to change the visualization options in AN-Smith.
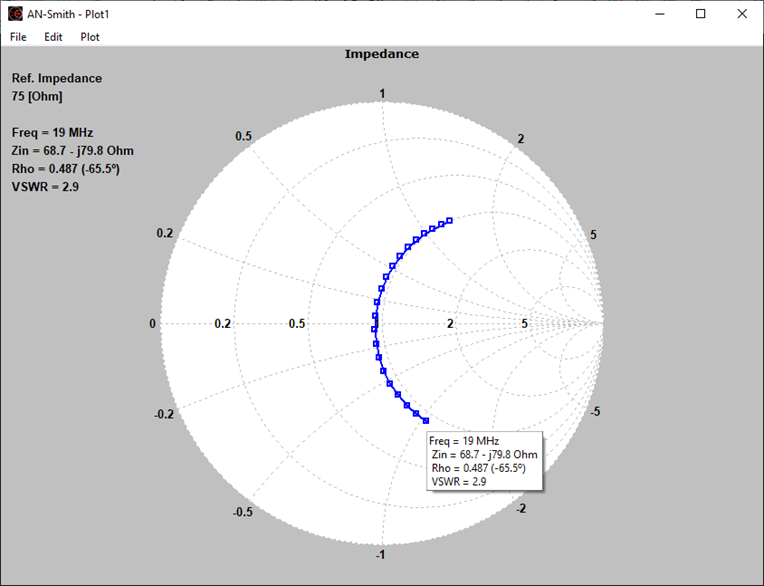
Antenna Feeder Calculator
In this article, you will learn how to add a feed line and transformer to your AN-SOF project. These components are essential for connecting your antenna structure to the external circuitry and impedance matching.
In the case of a transmitting antenna with a single feed port, the feeder used to connect the transmitter to the antenna terminals can be modeled in the Feeder tab, as shown in Fig. 1. The feeder consists of a transmission line, or feed line, and an impedance transformer.
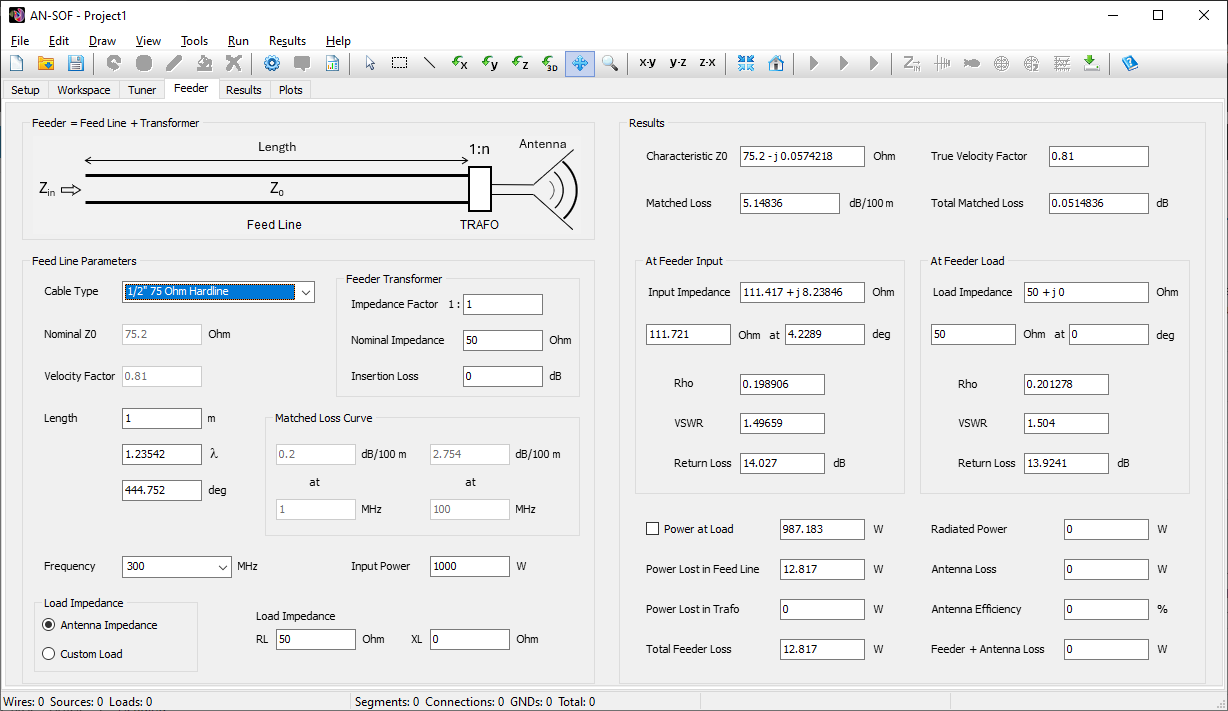
Setting the Impedance Transformer
The transformer, also known as trafo, can represent a balun or unun that connects directly to the antenna terminals to divide its input impedance by a factor, n. In the Feeder Transformer box, three parameters can be specified:
Impedance Factor 1:n
Here, “n” is the factor by which the antenna input impedance will be divided. For example, if we have a folded half-wave dipole, which typically has an input impedance on the order of 300 Ohms, we can set n = 4 to get 300/4 = 75 Ohms of input impedance after the transformer (i.e., a 1:4 balun). If the input impedance is complex, both its real and imaginary parts will be divided by n.
If the transformation factor is in the range 0 < n < 1, the transformer input impedance will be greater than the antenna impedance. By setting n = 1, we can represent a 1:1 transformer, also known as a common-mode choke or line isolator, used to transform a balanced or symmetrical antenna to an unbalanced feed line.
Note that “n” is the impedance transformer factor, not the voltage transformation factor. In a transformer, which is composed of a primary winding (inductor or coil) and a secondary winding, the voltage transformation factor is n-1/2.
Nominal Impedance
All actual impedance transformers, whether baluns or ununs, are fabricated for a nominal impedance, for which the manufacturer warranties the transformer performance in terms of bandwidth and insertion loss. So, if a lossy transformer is going to be modeled, we should set its nominal impedance according to the manufacturer’s datasheet.
Insertion Loss
The insertion loss of the transformer can be set in decibels to represent the actual loss given in its datasheet. The insertion loss is defined as the power lost, in decibels, inside the transformer, so that its output power will be lower than its input power due to losses in the transformer materials (coil resistivity, magnetic core losses, etc.).
Note: If no transformer is needed, just set n = 1 and an insertion loss of 0 dB.
Setting Feed Line Parameters
In AN-SOF, various real-life transmission line types are available, each with matched loss parameters adjusted according to the cable datasheets. These cable types are organized by part numbers and include the manufacturer’s name.
For example, entering “RG-8” in the Cable Type option will display this part number for different manufacturers, as shown in Fig. 2. Selecting RG-8 Belden 8237 will reveal a set of K0, K1, and K2 parameters. These constants have been adjusted to match the loss curve as a function of frequency, based on the matched loss vs. frequency table published in the cable datasheet. K0 relates to the DC losses in the transmission line conductors, K1 to the skin effect losses dependent on the square root of frequency, and K2 to dielectric losses increasing linearly with frequency. These losses are then considered in the standard RLGC model of a lossy transmission line.
The nominal values of the cable characteristic impedance Z0 and velocity factor will also be shown for the chosen part number and manufacturer. After selecting the cable type, you can set the operating frequency and input power to the feed line. The frequency can be chosen from a list that displays the frequencies set in the Setup tab.
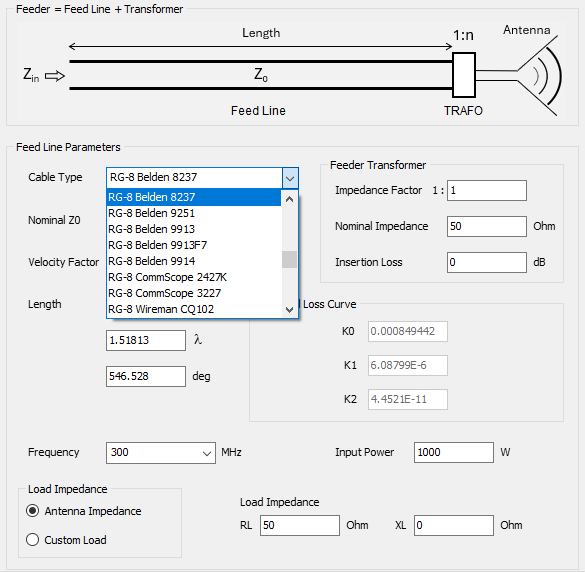
Next, you can set the length of the cable, entered according to the length unit used for drawing wires in the workspace. To change the length unit, go to Tools > Preferences in the main menu. As you type the cable length, the length measured in wavelengths (λ) and electrical degrees will be automatically displayed. In fact, all feed line results are calculated automatically by modifying any of the feed line parameters.
You can then choose the load impedance of the feed line. The default option considers the Antenna Impedance as the load impedance of the transmission line, automatically displaying the antenna input impedance at the chosen frequency as the load for the line. However, you can enter any value for the line load impedance by selecting the Custom Load option. This allows you to use the Feed Line tabsheet as an independent calculator for transmission lines.
After specifying the feeder parameters in the left side of the Feeder tab, the following results will be obtained in its right side (Fig. 1):
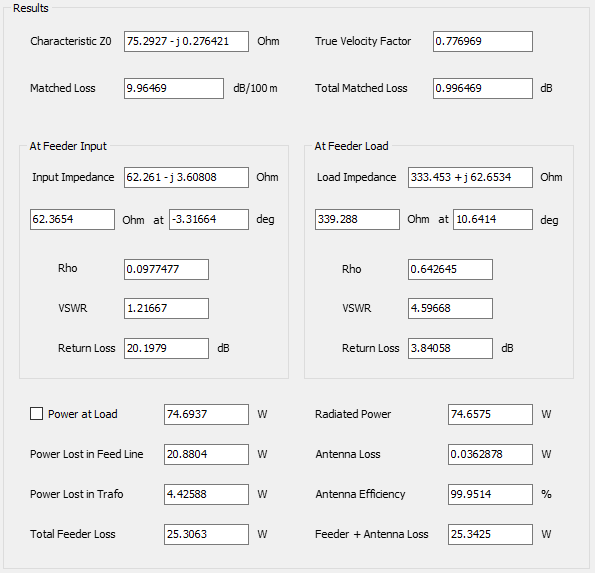
Characteristic Z0
This is the “true” characteristic impedance of the feed line obtained from the RLGC model via the K0, K1, and K2 constants. The real part of Z0 may differ somewhat from the nominal Z0 depending on frequency and losses in the transmission line. An imaginary part will always appear in Z0 due to non-zero losses. So, note that the true characteristic Z0 will generally differ from the “Nominal Z0” (Z0 in the cable datasheet).
True Velocity Factor
This is the “true” velocity factor obtained from the RLGC model of the transmission line, where the wavenumber (and wavelength inside the line) is affected by losses. The velocity factor will be modified relative to its nominal value accordingly. Therefore, the true velocity factor is a function of frequency and losses in the line.
Matched Loss
Any cable datasheet contains a table of matched loss values expressed in dB/100 feet or dB/100 m as a function of frequency. These values correspond to the attenuation of the line when it is matched (the line has a load impedance equal to Z0). So, the Matched Loss value shown in the Results panel is the attenuation of the line corresponding to the selected frequency.
Total Matched Loss
This is the matched loss that would be obtained for the specified length of the cable. Therefore, the Total Matched Loss equals the Matched Loss (dB/100 feet or dB/100 m) multiplied by the cable length.
At Feeder Input
The input impedance of the feeder (feed line + transformer) will be shown as well as the reflection coefficient (Rho), VSWR, and return loss, all referred to the true characteristic impedance of the feed line. This is the impedance at the feed line end opposite to the end where the load or antenna is connected.
At Feeder Load
The load impedance connected to the feeder (feed line + transformer) will be shown as well as the reflection coefficient (Rho), VSWR, and return loss, all referred to the true characteristic impedance of the feed line. The load impedance will be the antenna input impedance if the Antenna Impedance option was selected as a parameter for the feed line in the left side of the Feeder tab. If a “Custom Load” was selected, then the load impedance will be that entered by the user.
Power at Load
This is the power in Watts consumed at the feeder load impedance or effectively delivered to the antenna terminals. This power will be less than the input power specified as an input parameter for the feed line if the transmission line has losses. The power at the load will be equal to the input power in the case of a lossless transmission line. Check the Power at Load option to automatically set this power as the input power delivered to the antenna terminals. Otherwise, the antenna input power will be that set manually in the Excitation panel of the Setup tab.
Power Lost in Feed Line
This is the power lost along the transmission line in Watts.
Power Lost in Trafo
This is the power lost in the feeder transformer in Watts.
Total Feeder Loss
This is the sum of the powers lost in the feed line and in the transformer.
Radiated Power
This is the power in Watts radiated by the antenna when it is fed using the Power at Load, which is the power effectively delivered to the load impedance of the feeder. The radiated power will be different from the power delivered by the feeder if the antenna itself has its own losses. The radiated power will be shown if the option Antenna Impedance was selected as a load impedance for the feeder in the left side of the Feeder tab.
Antenna Loss
This is the power lost in the antenna structure. It will be shown if the option Antenna Impedance was selected as a load impedance for the feeder in the left side of the Feeder tab.
Antenna Efficiency
This is the ratio of the antenna radiated power to the antenna input power (the power delivered by the feeder). It is expressed as a percentage as it is usual. It will be shown if the option Antenna Impedance was selected as a load impedance for the feeder in the left side of the Feeder tab.
Feeder + Antenna Loss
This is the sum of the powers lost in the feeder (feed line + transformer) and antenna.
In addition to the manufactured cables listed in the Cable Type option, the following custom line options can be chosen, as shown in Fig. 1:
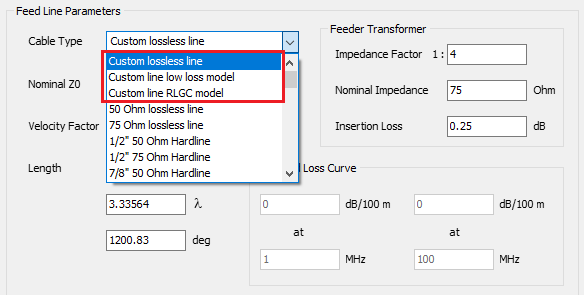
Custom lossless line
This option represents an ideal transmission line with zero losses. Only the nominal Z0 and velocity factor can be specified in this case.
Custom line low-loss model
This option allows the specification of the nominal Z0, velocity factor, and matched loss curve. To define the matched loss curve, two values of attenuation must be entered at two different frequencies, with the second frequency being greater than the first one. AN-SOF will adjust a low-loss model to obtain a curve of attenuation vs. frequency for subsequent calculations. While the real part of the characteristic Z0 will be equal to the nominal Z0 in the low-loss model, which is a good approximation in many cases, especially for higher frequencies, the characteristic impedance will have an imaginary part that depends on the line losses and frequency. The “true” velocity factor is also assumed to be equal to the nominal velocity factor.
Custom line RLGC model
This option represents a transmission line model where losses are accurately considered by adjusting a matched loss curve to the table of attenuation vs. frequency in the cable datasheet. The K0, K1, and K2 constants must be entered in this case. The definition of K0, K1, and K2 considers that the frequency is in Hz and lengths are in meters (SI metric units). This option allows the entry of K0, K1, and K2 obtained from other transmission line calculators.
Load Impedances
Follow these steps to select a wire segment that has a load and to tabulate the load impedance versus frequency,
- Right click on a wire that has a load to display the pop-up menu >.
- Click on the List Currents command to display the List Currents toolbar >.
- Move the slider and select the segment where the load is placed.
- Click on the Load List button to display the Load List dialog box, where the list of currents, voltages, and powers in the load impedance versus frequency is shown. Select an item from the list in the upper right corner of the window and then press the Plot button to plot the selected item versus frequency.
Follow these steps to select a wire segment that has a source and to tabulate the source internal impedance versus frequency,
- Right click on a wire that has a source to display the pop-up menu >.
- Click on the List Currents command to display the List Currents toolbar >.
- Move the slider and select the segment where the source is placed.
- Click on the Source List button to display the Source List dialog box, where the list of currents, voltages, and powers in the internal impedance of the source versus frequency is shown. Select an item from the list in the upper right corner of the window and then press the Plot button to plot the selected item versus frequency.
Far Field
The radiation pattern can be visualized as a 2D rectangular plot by selecting Results > Plot Far-Field Pattern > 2D Rectangular Plot from the main menu. This action will open the Radiation Pattern Cut dialog box (Fig. 1), where two plot types are available:
- Conical Plots: Generated with a fixed Theta and variable Phi.
- Vertical Plots: Created with a fixed Phi and variable Theta.
Select a radiation pattern cut and click OK to launch the AN-XY Chart application (Fig. 2), where the radiation pattern is plotted against Phi for conical plots (fixed Theta) or against Theta for vertical plots (fixed Phi).
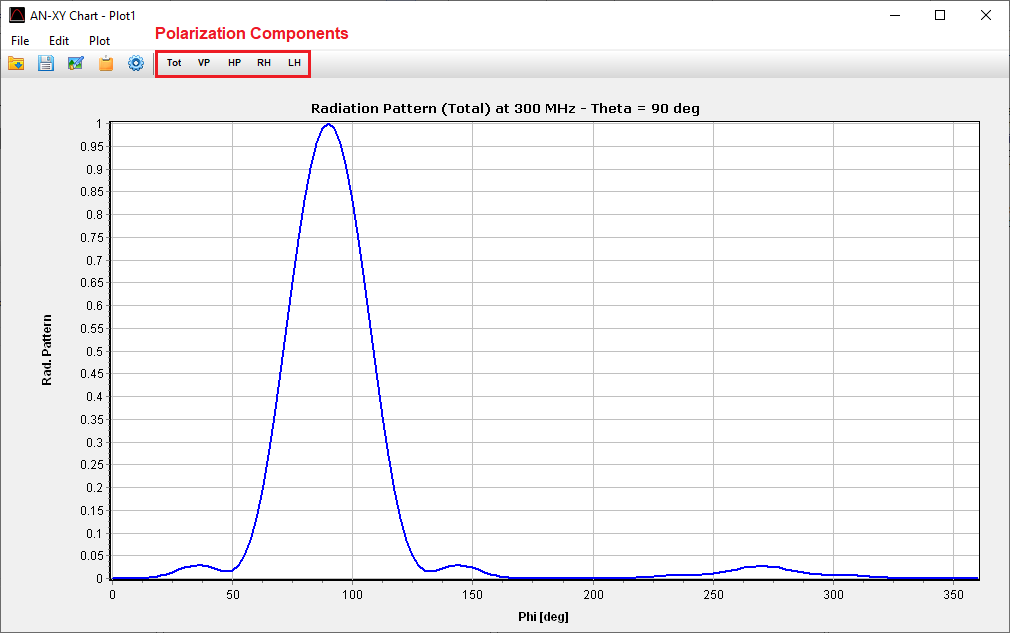
Within the AN-XY Chart app, access the Plot menu to graph various parameters, including Power Density, Directivity, Gain, E-field, and Axial Ratio. This menu also allows you to represent these metrics in decibels (dBi for directivity and gain) and decompose them into linearly polarized components: Theta (VP: Vertically Polarized) and Phi (HP: Horizontally Polarized), as well as circularly polarized components: Right (RHCP: Right-Handed Circularly Polarized) and Left (LHCP: Left-Handed Circularly Polarized). The app’s toolbar features buttons: Tot, VP, HP, RH, and LH for quick switching between the total field metric and its corresponding polarization components. For instance, you can plot the total gain in dBi or decompose it into its Theta (VP), Phi (HP), Right (RHCP), or Left (LHCP) components to analyze antenna polarization characteristics.
In the case of plane wave excitation, where the antenna is receiving or the metallic structure is scattering electromagnetic waves, the Radar Cross Section (RCS) will be plotted instead of directivity and gain. The resulting radiation pattern is the scattered field pattern, observed in the far-field region where the scattered field amplitude decays with the inverse of the distance (1/r), and the scattered power density decays with the inverse square of the distance (1/r²) from the structure.
The Axial Ratio is defined as the ratio of the minor axis to the major axis of the polarization ellipse. It ranges from 0 to 1 in absolute value and can also be plotted in decibels. A circularly polarized field exhibits an axial ratio of ±1 (or 0 dB), while a linearly polarized field has an axial ratio of zero. A positive (negative) axial ratio indicates a right-handed (left-handed) polarized field.
The far-field pattern can also be visualized in a 2D polar chart by selecting Results > Plot Far-Field Pattern > Polar Plot 1 Slice from the AN-SOF main menu (refer to Fig. 3). This action will launch the AN-Polar app, which displays information such as maximum radiation, beamwidth, and front-to-rear/back ratios.
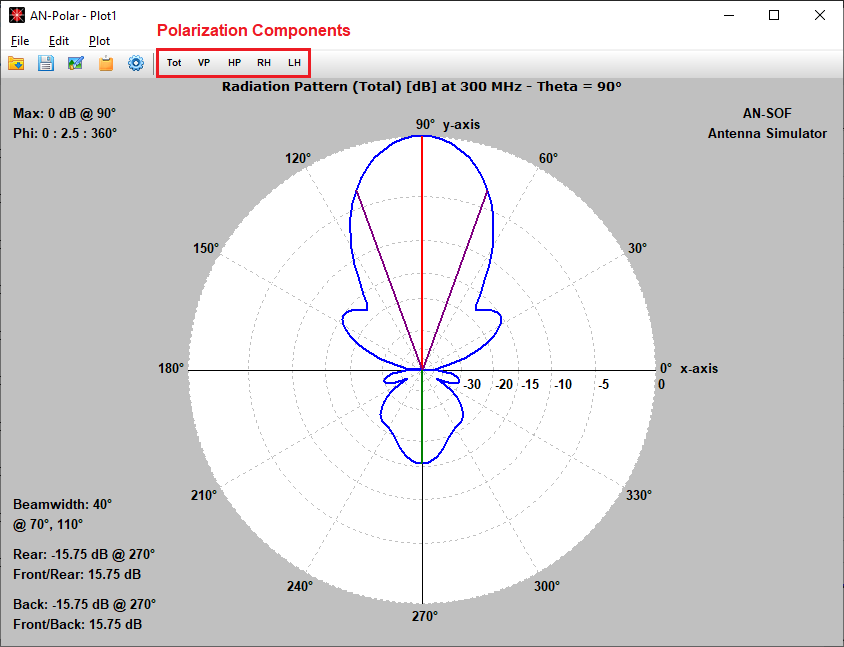
The AN-Polar app also features a toolbar with buttons: Tot, VP, HP, RH, and LH that enable the decomposition of the plotted metric into its polarization components.
To plot two slices of a 3D far-field pattern on the same polar chart, navigate to Results > Plot Far-Field Pattern > Polar Plot 2 Slices in the AN-SOF main menu. A dialog box will appear, allowing you to select the two slices. You can choose from two vertical slices, two conical slices, or vertical-conical combinations (see Fig. 4).
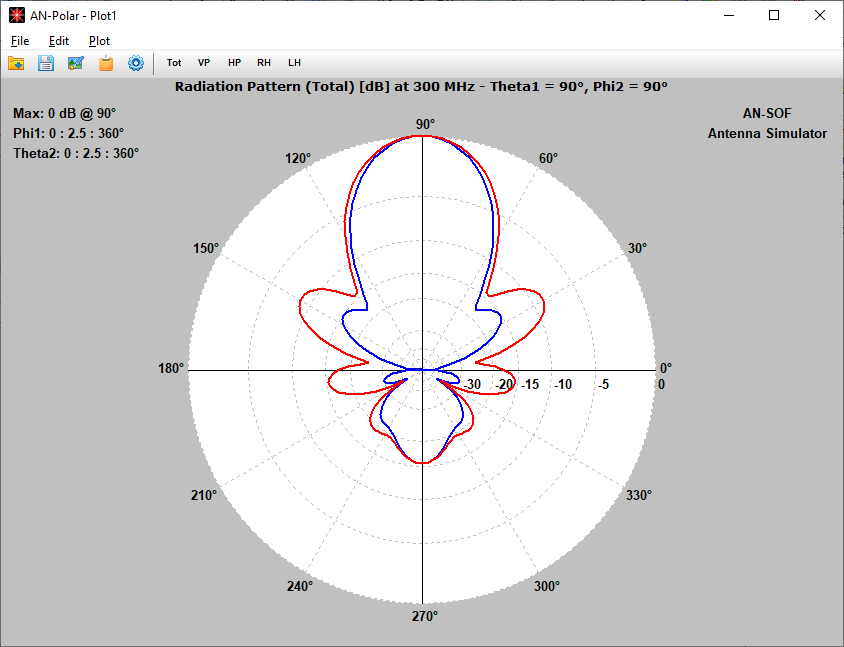
Clicking on a point in the polar curve will display the corresponding value of the represented metric and the polar angle.
When plotting a single slice of the radiation pattern, the AN-Polar application automatically displays key performance metrics—beamwidth, Front-to-Back ratio, Front-to-Rear ratio, and their corresponding angles—in the lower-left corner of the window. For definitions and practical explanations of these metrics, refer to the article:
The far-field can be visualized as a 3D plot by selecting Results > Plot Far-Field Pattern > 3D Plot from the AN-SOF main menu. This action will open the AN-3D Pattern application, where the radiation pattern is displayed in a 3D view, showcasing the radiation lobes with their intensities represented by a color scale.
Within the AN-3D Pattern application, access the Plot menu to select the Power Density, Directivity (numerical and in dBi), Gain (numerical and in dBi), Radiation Pattern (normalized to unity and to 0 dB), E-field, and Axial Ratio (dimensionless and in dB) (see Fig. 1). Each field metric can be decomposed into its linearly polarized components Theta (VP: Vertical Polarization) and Phi (HP: Horizontal Polarization), as well as its circularly polarized components Right (RHCP: Right-Handed Circular Polarization) and Left (LHCP: Left-Handed Circular Polarization).
If the simulation involves plane wave excitation, the Radar Cross Section (RCS) can be plotted instead of directivity and gain. The resulting radiation pattern is the scattered field pattern, observed in the far-field region where the scattered field amplitude decays with the inverse of the distance (1/r), and the scattered power density decays with the inverse square of the distance (1/r²) from the structure.
The Axial Ratio pattern is defined as the ratio of the minor to major axis of the polarization ellipse. It equals 0 for a linearly polarized field and 1 for a circularly polarized field. While lobes in a 3D polar plot can only represent absolute values, the sign of the axial ratio, which determines whether the field is RHCP or LHCP, cannot be directly visualized here but can be observed in a 2D rectangular plot. However, the toolbar in the AN-3D Pattern application features buttons: Tot, VP, HP, RH, and LH for quick switching between the total field and its polarization components, facilitating polarization analysis.
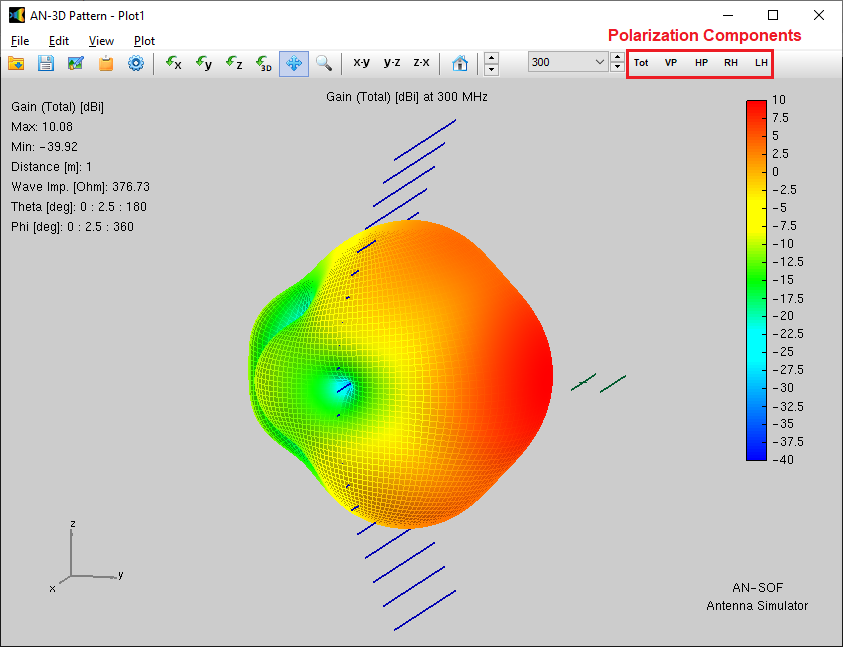
The 3D graph can be rotated and moved by clicking the “3D Rotation” or “Move” buttons on the toolbar and then dragging the mouse with the left button pressed. Use the mouse wheel to zoom in or out. The AN-3D Pattern toolbar also includes an option to change the frequency and dynamically observe the changes in the radiation pattern lobes as a kind of animation (use the up-down arrow buttons next to the displayed frequency value).
Note
- If discrete sources were used as the excitation of the structure, the plotted far-field represents the total field.
- If an incident plane wave was used as the excitation, the plotted far-field represents the scattered field.
To access the Preferences dialog box in the AN-3D Pattern main menu, click on Edit > Preferences (refer to Fig. 2). This dialog box allows you to customize various options for the colored surface and mesh of the radiation lobes (see Fig. 3). Additionally, you can superimpose the wire structure onto the radiation pattern by selecting the Wires option in the “Show” box. You also have control over the graph’s scale and can display the main axes.
The radiation pattern cannot be directly exported from the AN-3D Pattern application. However, the far-field pattern for a specific frequency can be tabulated by navigating to the AN-SOF main menu > Results > List Far-Field Pattern and then pressing the “Export” button next to the displayed table to export the data to a CSV (Comma Separated Values) file.
Far-field frequency spectra are generated when a simulation is run using either a specified list of frequencies or a frequency sweep. At each frequency, the far field is calculated over a range of directions defined by the zenith (Theta) and azimuth (Phi) angles, as well as the observation distance set in the Far-Field panel of the Setup tab. To plot the far field as a function of frequency, you must first choose a fixed direction—i.e., specific Theta and Phi angles.
To generate the far-field spectrum plot, go to Results > Plot Far-Field Spectrum in the main menu. This will open the Select Far-Field Point dialog box (see Fig. 1), where you can specify the desired Theta and Phi angles. After clicking OK, the AN-XY Chart application will display the far-field spectrum versus frequency (see Fig. 2).
In the Plot menu of the AN-XY Chart application, various far-field metrics are available, including Power Density, Directivity, Gain, Radiation Pattern, E-Field, and Axial Ratio. Most of these metrics can be displayed in decibels and support polarization decomposition into VP (Vertically Polarized), HP (Horizontally Polarized), RHCP (Right-Hand Circularly Polarized), and LHCP (Left-Hand Circularly Polarized) components. The toolbar offers quick access to toggle between these polarization components (see Fig. 3).
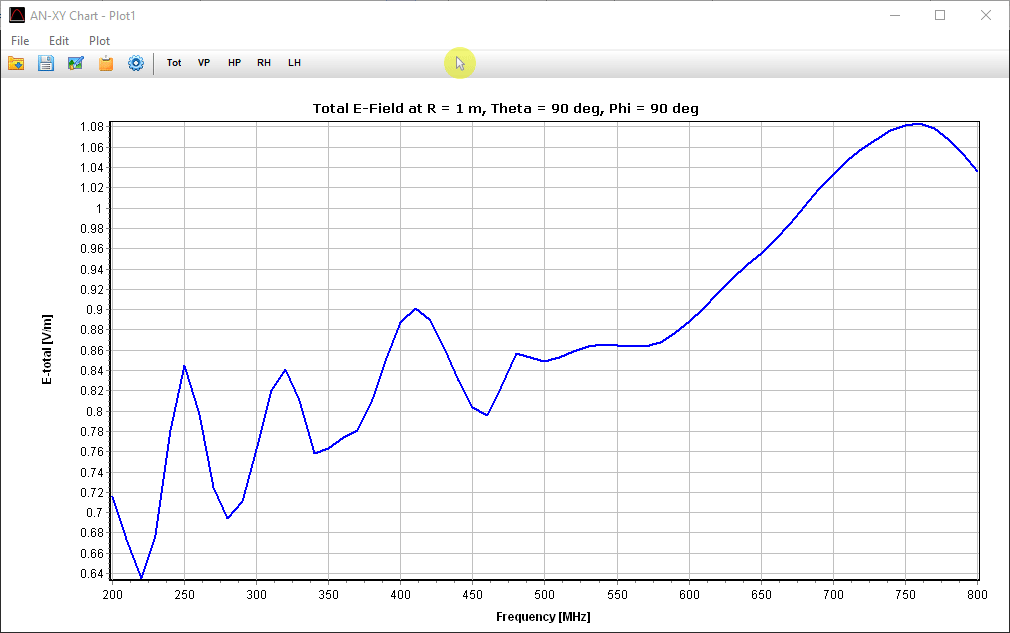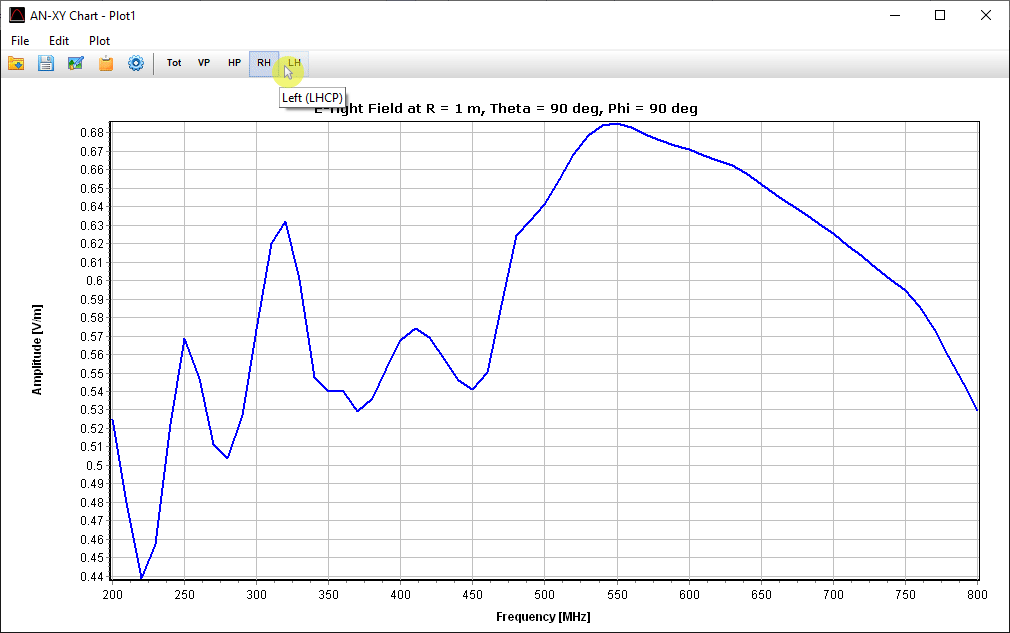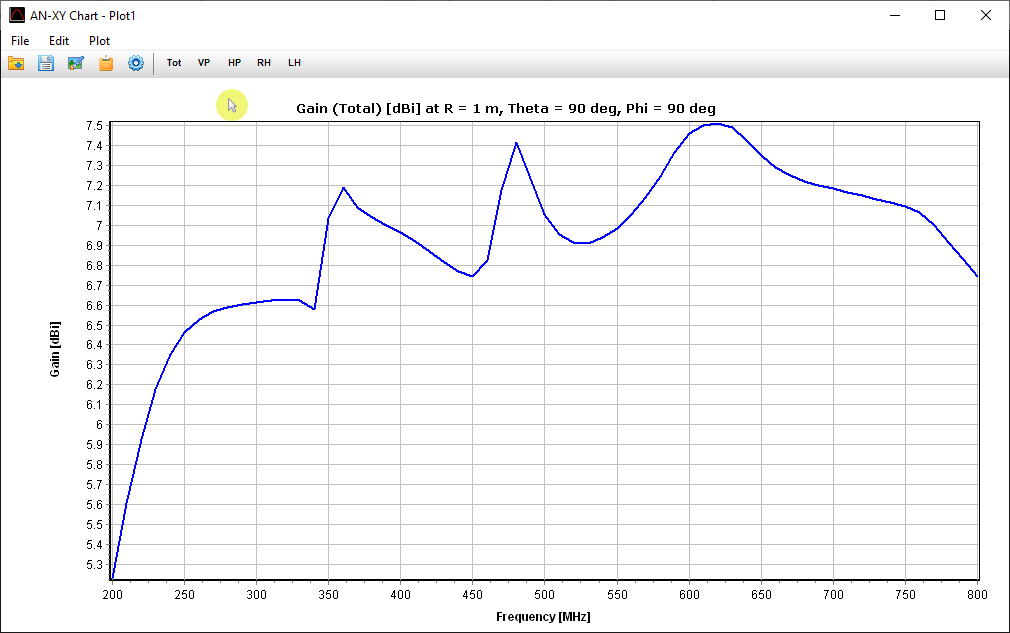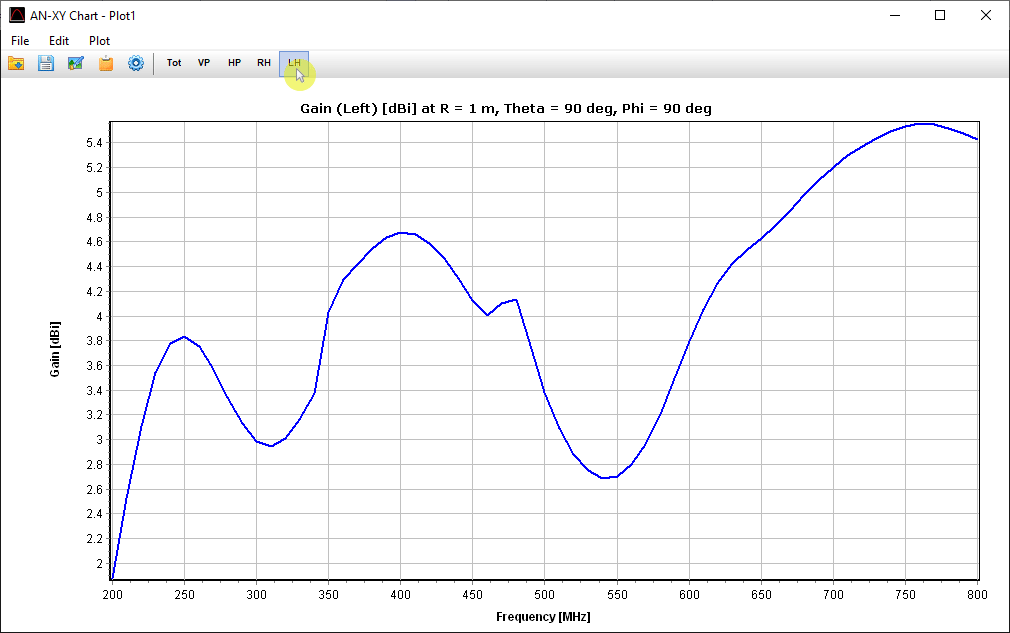
You can also plot the linearly polarized electric field components (E-Theta and E-Phi) and the circularly polarized components (E-Right and E-Left) versus frequency. Each component can be displayed in terms of amplitude, phase, or real and imaginary parts. Additionally, the Axial Ratio—defined as the ratio of the minor to major axes of the polarization ellipse—can be plotted as a function of frequency, in both linear scale and decibels.
The far-field spectrum at a selected observation point can also be displayed in tabular form. To do this, go to Results > List Far-Field Spectrum in the AN-SOF main menu. This will open the Select Far-Field Point dialog box, where you can specify fixed values for Theta and Phi. Once selected, a table listing the far-field components versus frequency will be displayed. You can then click the Plot button to visualize the data (see Fig. 4). This set of tools offers valuable capabilities for analyzing far-field behavior across frequencies.
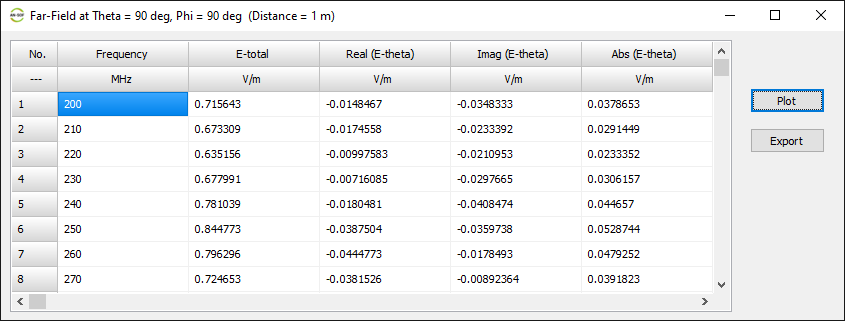
To access the Power Budget dialog box (see Fig. 1), navigate to Results > Power Budget/RCS in the main menu. When discrete sources are used for excitation, the following list of parameters versus frequency is displayed:
Parameters
- Input Power: Total input power provided by the discrete sources in the structure.
- Radiated Power: Total radiated power from the structure.
- Structure Loss: Total consumed power, representing ohmic losses in the structure.
- Efficiency: Radiated power-to-input power ratio, representing the radiation efficiency. For a lossless structure, this value is 100%.
- Directivity: Peak directivity, displayed both as a dimensionless value and in decibels (dBi) relative to an isotropic source.
- Gain: Peak gain, displayed both as a dimensionless value and in decibels (dBi) relative to an isotropic source.
- Av. EIRP (Effective Isotropic Radiated Power): Time-averaged EIRP in Watts and dBW. This value accounts for the duty cycle of the selected transmit mode in the Tuner tab and the Time Transmitting percentage.
- Peak EIRP (Effective Isotropic Radiated Power): Peak EIRP in Watts and dBW, calculated directly from the Peak Envelope Power (PEP) without considering the duty cycle or time transmitting percentage.
- Av. Power Density: Average power density, calculated by averaging the power density over all directions in space.
- Peak Power Density: Maximum value of the radiated power density.
- Theta (max) and Phi (max): The zenith and azimuth angles, respectively, in the direction of maximum radiation, corresponding to the peak power density.
- F/R H and F/B H: Front-to-rear and front-to-back ratios, respectively, in a horizontal slice of the radiation pattern given by Theta = Theta (max).
- F/R V and F/B V: Front-to-rear and front-to-back ratios, respectively, in a vertical slice of the radiation pattern given by Phi = Phi (max).
Error and Average Gain Test (AGT)
- Error: Represents the error in the power balance of the system. A necessary (but not sufficient) condition for a valid model is that the input power must equal the sum of the radiated and lost powers. The error is calculated as:
$\displaystyle \text{Error %} = 100 \times \frac{\text{Input Power} \,-\, \text{Lost Power} \,-\, \text{Radiated Power}}{\text{Input Power} \,-\, \text{Lost Power}}$
- Average Gain Test (AGT): A validation metric that should be close to 1 for a valid model. It is calculated as:
$\displaystyle \text{AGT} = \frac{\text{Radiated Power} + \text{Lost Power}}{\text{Input Power}}$
Plotting and Exporting Data
- Select an item from the list in the upper-right corner of the window and click the Plot button to plot the selected item versus frequency.
- Click the Export button to export the list to a CSV file.
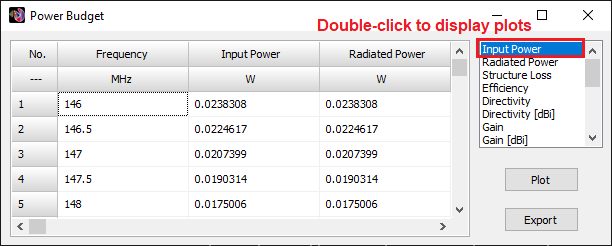
Notes
- A power budget error of about ±10% is permissible from the engineering point of view.
- When a real ground plane is used, the Error column shows the percentage of power lost in the ground due to its finite conductivity.
- When a substrate slab is used, this column shows the percentage of power transferred to the dielectric material in the substrate (surface wave loss).
- AGT = 1 means that the power balance is exact. An AGT between 0.99 and 1.01 is comparable to achieving an error of ±1%.
To access the Radar Cross Section dialog box (see Fig. 1), go to Results > Power Budget/RCS in the main menu. The following list of parameters versus frequency is displayed when an incident field is used for excitation:
- The RCS [m2] column shows the Radar Cross Section in square meters.
- The RCS [lambda2] column shows the Radar Cross Section in square wavelengths.
- The RCS [dBsw] column shows the Radar Cross Section in decibels with reference to a square wavelength.
- The Radiated Power column shows the total scattered power from the structure.
- The Structure Loss column shows the total consumed power, representing ohmic losses in the structure.
- The Av. Power Density column displays the average power density scattered from the structure. This value is computed by averaging the scattered power density over all directions in space.
- The Peak Power Density column shows the maximum value of the scattered power density.
- The Theta (max) and Phi (max) columns represent the zenith and azimuth angles, respectively, in the direction of maximum radiation.
These radiation pattern metrics corresponds to the scattered field pattern, observed in the far-field region where the scattered field amplitude decays with the inverse of the distance (1/r), and the scattered power density decays with the inverse square of the distance (1/r²) from the structure.
Select an item from the list in the upper right corner of the window and then press the Plot button to plot the selected item versus frequency.
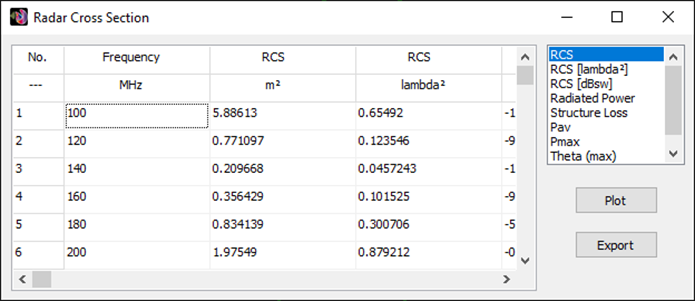
The far field patterns and spectra can be tabulated and exported by going to the following commands in the Results menu >:
- List Far-Field Pattern
- List Far-Field Spectrum
A table with the results will be displayed after executing any of these commands, Fig. 1. The tabulated values can be exported to a CSV (Comma Separated Values) file by clicking the Export button.
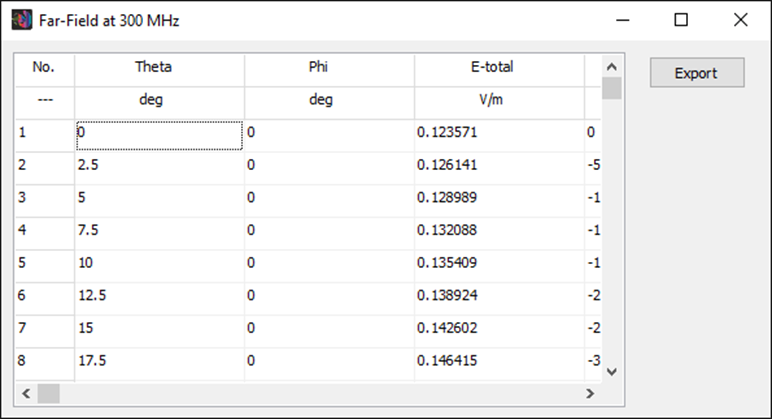
Near Field
The grid of points where the near field is calculated can be specified in the Near-Field panel of the Setup tab. There, the points can be entered in Cartesian, Cylindrical, or Spherical Coordinates. The near electric (E) and magnetic (H) fields can be calculated separately. Of course, the near fields can be calculated in any region of an antenna, very close to it or far away. In the far-field region, the near fields will tend to the known behavior of far-fields: E and H are perpendicular to each other and perpendicular to the radial direction from the antenna, they oscillate in phase, and their magnitudes have a constant ratio: E/H ≈ 377 Ohms (often also approximated as 120π Ohms) in free space. This behavior can be verified by performing calculations of the “near” E and H fields far from an antenna.
When both E and H fields have been calculated, the power density (S) will also be available in tables and plots. The total rms power density is calculated as S = |E x H*|. This metric is particularly important for assessments to evaluate electromagnetic field compliance with radiation exposure limits published by regulatory authorities.
To plot the near electric field as a 3D graph with a color scale, go to Results > Plot Near E-Field Pattern > 3D Plot in the main menu. This command executes the AN-3D Pattern application (Fig. 1). To display a 3D plot of the near magnetic field or power density, respectively, go to Results > Plot Near H-Field Pattern > 3D Plot or Results > Plot Power Density Pattern > 3D Plot.
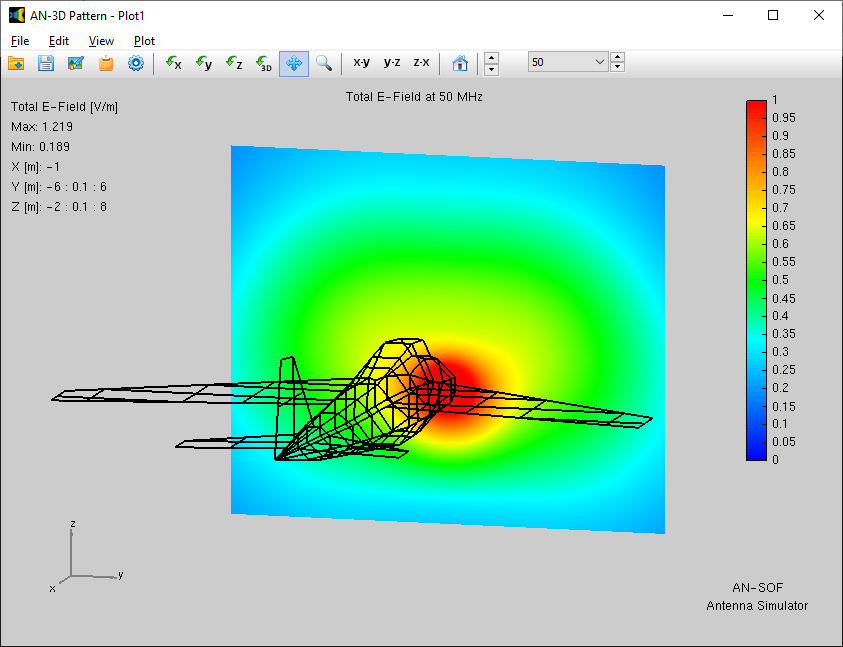
Near-field 3D plots will be shown according to the type of coordinate system chosen in the Near-Field panel of the Setup tab: Cartesian, Cylindrical, or Spherical. If near-fields were calculated for more than one frequency, a dialog box asking for a fixed frequency will be shown before plotting the near-field pattern.
The near electric field can also be plotted as a 2D rectangular plot by going to Results > Plot Near E-Field Pattern > 2D Plot in the main menu. The near magnetic field can be plotted by going to Results > Plot Near H-Field Pattern > 2D Plot, and the power density by going to Results > Plot Power Density Pattern > 2D Plot. These commands execute the AN-XY Chart application, where the total rms electric field, magnetic field, or power density is plotted in a 2D chart (Fig. 2). The components of the near E and H fields can be plotted individually by going to the Plot menu in the AN-XY Chart and selecting the desired component.
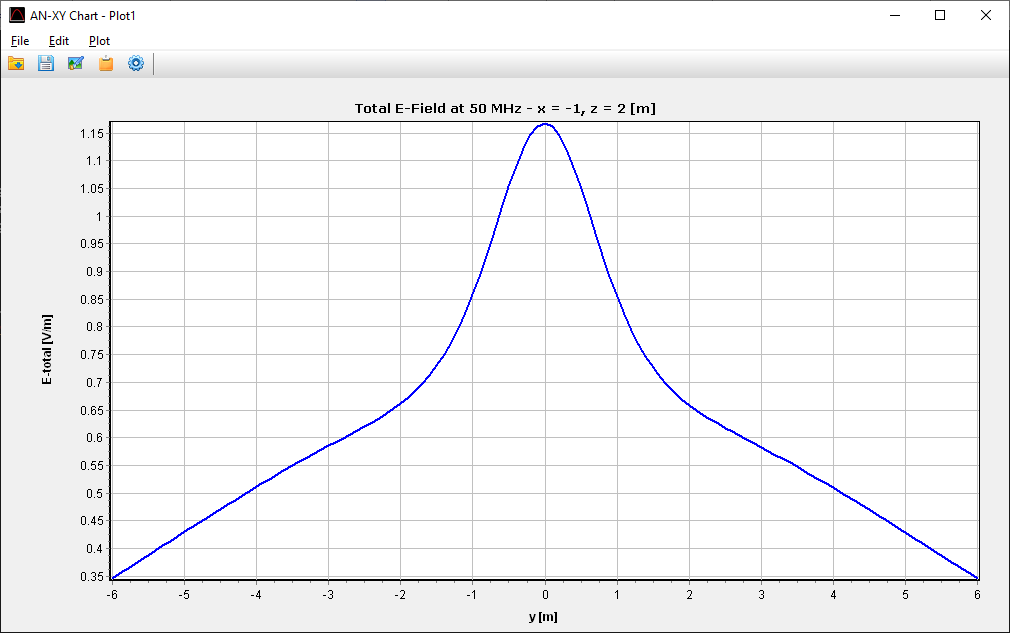
The near-field patterns for a given frequency can also be tabulated by going to Results > List Near E-Field Pattern, Results > List Near H-Field Pattern, or Results > List Power Density Pattern in the AN-SOF main menu.
Regarding the E and H Field Components
- If Cartesian coordinates have been set in the Near-Field panel of the Setup tab, the Ex, Ey, and Ez electric field components and the Hx, Hy, and Hz magnetic field components will be calculated in a rectangular grid of points in space with coordinates (x, y, z).
- If Cylindrical coordinates have been set in the Near-Field panel of the Setup tab, the Er, Ephi, and Ez electric field components and the Hr, Hphi, and Hz magnetic field components will be calculated in a cylindrical grid of points in space with coordinates (r, phi, z).
- If Spherical coordinates have been set in the Near-Field panel of the Setup tab, the Er, Etheta, and Ephi electric field components and the Hr, Htheta, and Hphi magnetic field components will be calculated in a spherical grid of points in space with coordinates (r, theta, phi).
Near-field frequency spectra are obtained when a simulation is performed by specifying a list of frequencies or a frequency sweep. For each frequency, the near field is calculated at the points specified in the Near-Field panel of the Setup tab. Therefore, a fixed point in space must be selected to plot the near field versus frequency (the near field spectrum).
To plot the near E-field, near H-field, or power density spectrum, go to Results > Plot Near E-Field Spectrum, Results > Plot Near H-Field Spectrum, or Results > Plot Power Density Spectrum in the main menu. These commands display the Select Near-Field Point dialog box, where a fixed observation point can be selected (Fig. 1). The AN-XY Chart application will then show the frequency spectrum of the selected field (Fig. 2). The E and H field components can be plotted in amplitude, phase, real, and imaginary parts by choosing these options under Plot in the AN-XY Chart main menu.
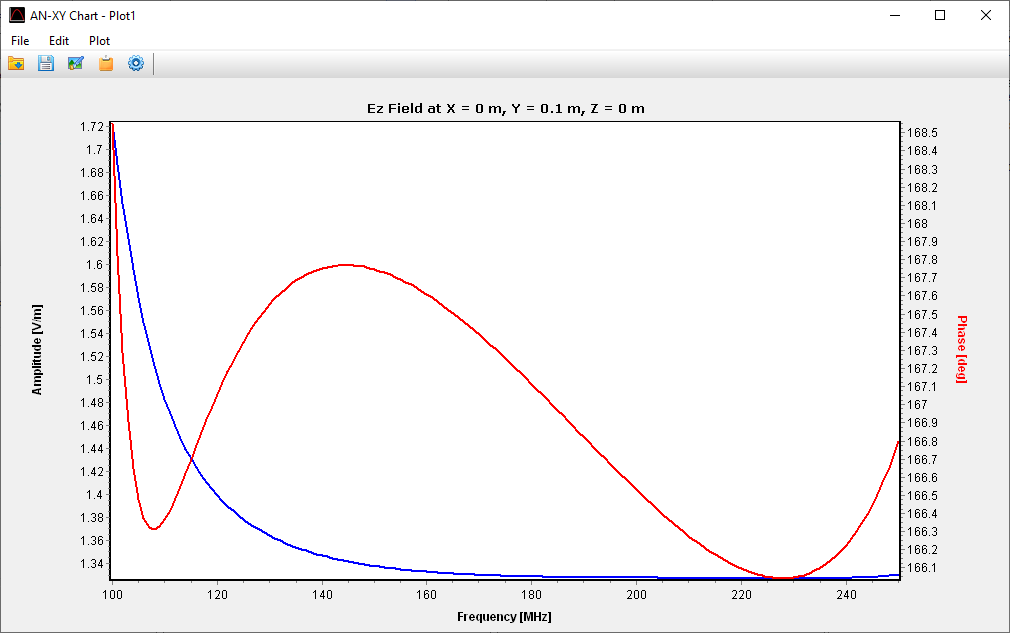
Near field patterns and spectra can be tabulated and exported by going to the following commands in the Results menu >:
- List Near E-Field Pattern
- List Near E-Field Spectrum
- List Near H-Field Pattern
- List Near H-Field Spectrum
A table with the results will be displayed after executing any of these commands. The tabulated values can be exported to a CSV (Comma Separated Values) file by clicking the Export button.
Transmission Lines
Adding a transmission line to a model has an impact on the entire calculation, affecting current distribution, input impedance, and near and far fields. AN-SOF allows for the addition of lossy or lossless transmission lines and has a list of preloaded lines with parameters adjusted to the attenuation curves published in the data sheets of real cables. This list of cables includes both two-wire and coaxial transmission lines.
After drawing and segmenting the wire structure that will represent an antenna or an object that will scatter electromagnetic waves, the recommended first step is to create a list of the transmission lines that will be connected to the structure. This is described below.
The ends of a transmission line in AN-SOF are called Port 1 and Port 2 since a line can be considered as a two-port network. Each end or port of a transmission line can be connected to a segment of the wire structure, as Fig. 1 shows. A transmission line is defined by its characteristic impedance, Z0, velocity factor, VF, a loss model or attenuation curve, and shunt admittances, Y1 and Y2, connected across each port. Each transmission line must be connected between two different wire segments (the i-th and j-th segments in Fig. 1 should not be the same segment). In the calculation engine model, a gap is opened in the center of each segment to allow a transmission line to be connected there.
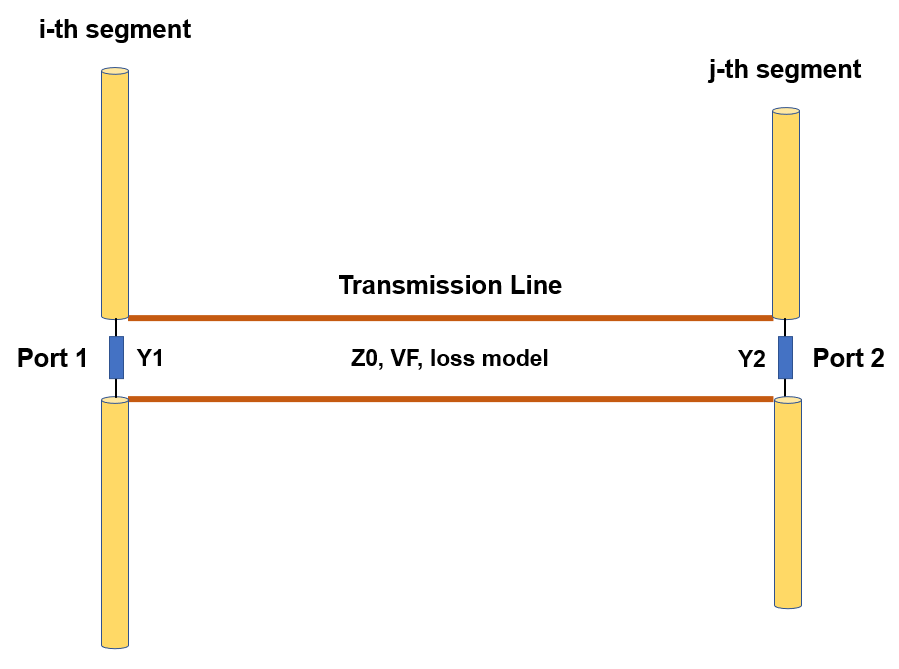
Transmission lines are modeled in an implicit way, meaning that the lines don’t scatter electromagnetic waves in space, but rather interact with the wire structure by establishing boundary conditions on the voltages and currents at the connected segments. Implicit modeling is adequate when the disturbance in the electromagnetic field caused by the physical presence of the transmission line can be neglected, e.g., for twisted-pair lines in most cases. On the other hand, explicit modeling involves drawing the two parallel wires of a two-wire line in the workspace and dividing them into segments, like the rest of the structure. For coaxial lines, a “hybrid” modeling approach can be used, which is explained in Modeling Coaxial Cables.
To add transmission lines, go to the AN-SOF main menu > Draw > Transmission Lines (Ctrl + L). A table will be displayed where a transmission line can be entered on each row. Follow the procedure below to enter the lines:
- Select a row by clicking on the row number of your choice in the first column labeled ‘No.’, Fig. 2.
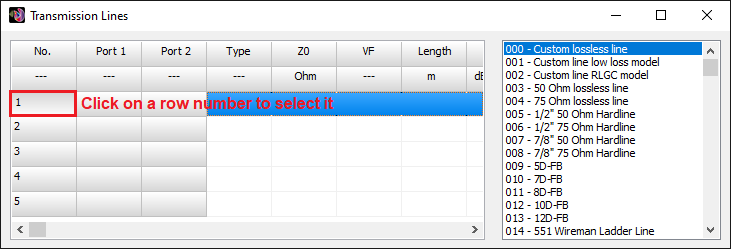
- On the right-hand panel, choose a type of transmission line and double-click on your chosen type. The selected row will be automatically completed, Fig. 3.

- From type 3 onwards, the parameters correspond to real cable datasheets. If you wish to enter your own parameters, choose types 0, 1, or 2. To edit the value in a cell, double-click on the cell.
Note that in this procedure, the ports of the transmission lines have not been connected to the wire segments yet. This is explained in Connecting Transmission Lines.
The parameters that define a transmission line are:
1) Type: On the right-hand panel of the Transmission Lines window, there is a list of lines with the cable part number and the manufacturer in some cases. The first three types are used to input user-customized lines. The line type simply refers to its position in this list.
2) Z0: Nominal characteristic impedance, in Ohms. If a negative value is entered, the transmission line will be “crossed” with a 180° phase reversal with respect to the reference directions of the segments (the characteristic impedance of the line will of course be |Z0|).
3) VF: Velocity factor (dimensionless). The allowed range is 0 < VF <= 1.
4) Length: Length of the line, in the unit selected in the Preferences window (see Section “3.3 Preferences”). If a length of zero is entered, the length of the transmission line will be equal to the linear distance between the two wire segments connected at the ends of the line.
5) The K0, K1, K2, and K3 columns define the line losses for the so-called RLGC model. These four columns will change to Att. 1, Freq. 1, Att. 2, Freq. 2 when the chosen line model is that of low losses. These cells allow entering the attenuation curve of a real transmission line from its datasheet.
6) Real(Y1) and Imag(Y1) are the real and imaginary parts of the shunt admittance through Port 1 of the transmission line, in Siemens [S].
7) Real(Y2) and Imag(Y2) are the real and imaginary parts of the shunt admittance through Port 2 of the transmission line, in Siemens [S].
A transmission line without shunt admittances (Y1 = Y2 = 0) will always be symmetrical in the sense that if it is connected in reverse, i.e., by swapping ports 1 and 2, the same results will be obtained in a simulation. Ports 1 and 2 are identified so that the locations of the shunt admittances can be distinguished when they are not zero.
If you enlarge or maximize the Transmission Lines window, you will be able to see the columns corresponding to the loss model parameters and shunt admittances, Figs. 4 and 5. Initially, this window only displays cells up to the ‘Length’ column so that the user does not have to worry about the loss parameter values since these are automatically loaded when selecting a line type from the list. Adding an attenuation curve when modeling a cable that is not on the list is explained in Adding a Custom Lossy Line.


If you want to add “custom” transmission lines with your own parameters, you have types 0, 1, and 2 available, Fig. 1, which are explained below.
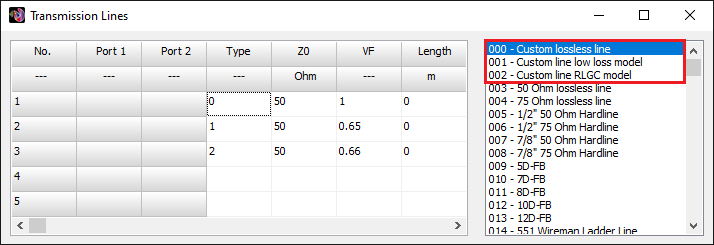
Type 0: Custom Lossless Line
This is an ideal transmission line with zero losses, so only the nominal Z0 and velocity factor must be specified.
Type 1: Custom line – low loss model
This is a transmission line where the nominal Z0, velocity factor, and matched loss curve can be specified. To define the matched loss curve, two attenuation values must be entered at two different frequencies, with the second frequency being greater than the first. AN-SOF will then adjust a low-loss model to obtain an attenuation vs. frequency curve for subsequent calculations. This is the simplest way to enter parameters from the datasheet of a manufactured real transmission line. Refer to Adding a Custom Lossy Line where it explains how to add the parameters from an attenuation curve published in a datasheet of a real cable.
Type 2: Custom line – RLGC model
This is a transmission line model that considers losses by adjusting a matched loss curve to the table of attenuation vs. frequency in the cable datasheet. The K0, K1, and K2 constants must be entered in this case. The definition of K0, K1, and K2 assumes that the frequency is in Hz and the lengths are in meters (SI metric units). This option allows for the entry of K0, K1, and K2 obtained from third-party transmission line calculators (K3 is an additional constant that is zero for all available cables).
Any transmission lines added through the Transmission Lines command (Ctrl + L) under the Draw menu will remain in the table until the user decides to remove or modify them. During calculations, only transmission lines with both ports connected to respective wire segments will be considered for simulation. Any lines with a single port connected or both ports disconnected will be omitted in the calculations.
To connect a transmission line between two wire segments, follow these steps:
- Right-click on the first wire to select it and choose the Source / Load / TL (Ctrl + Ins) command from the pop-up menu. This will open a horizontal toolbar with a slider control, Fig. 1.
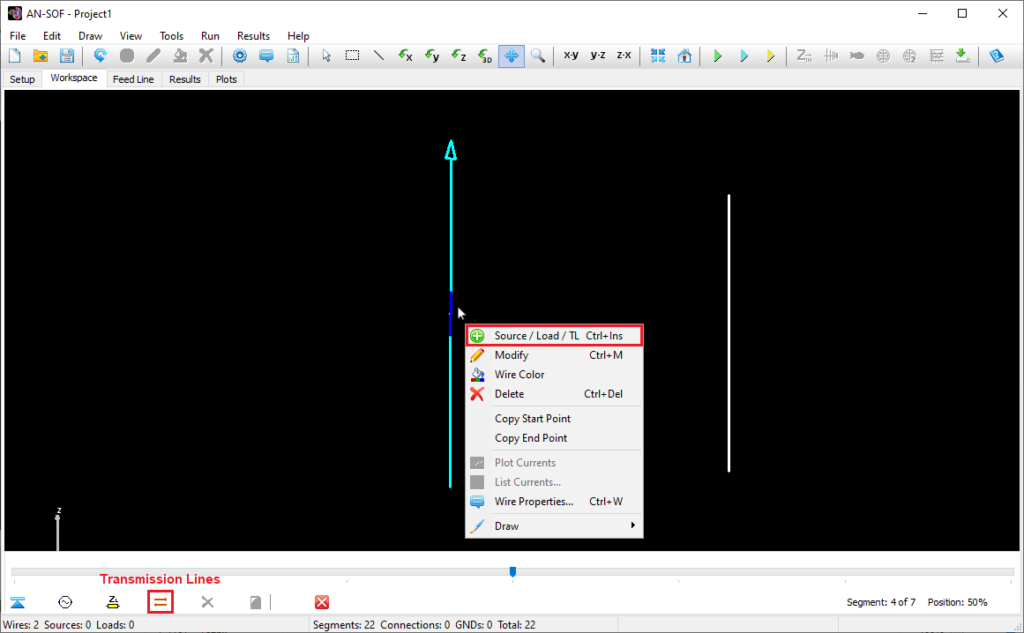
- Use the slider to select the specific segment of the first wire to which you want to connect a port of the transmission line.
- Once you’ve chosen the segment, click on the Transmission Lines button on the horizontal toolbar to open the Transmission Lines table, Fig. 2.
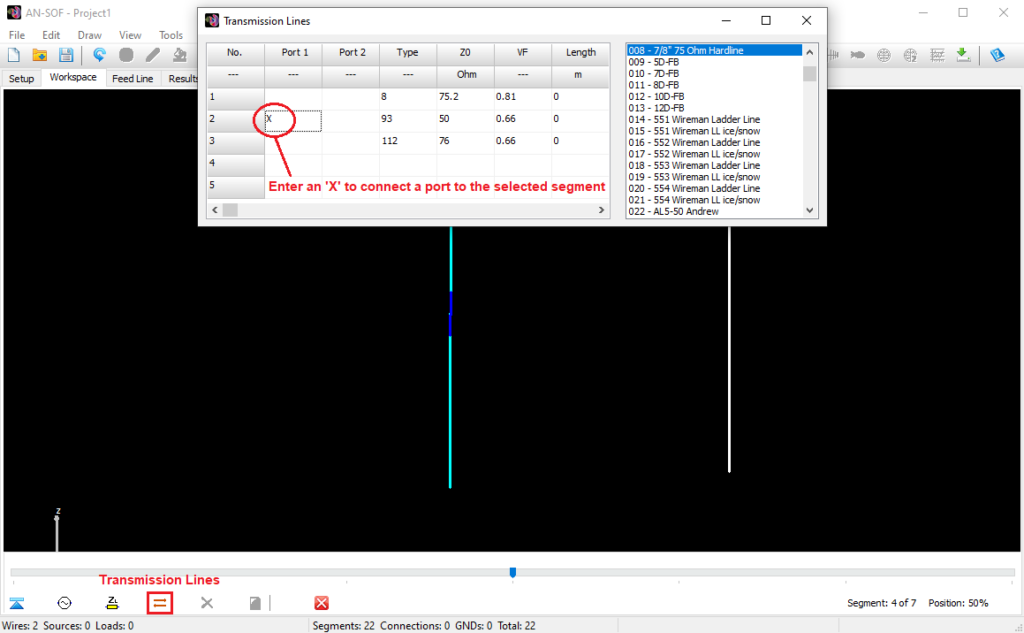
- Enter an “x” or “X” (without quotes) in the corresponding cell for the port you want to connect to the selected segment (the cells located below the “Port 1” and “Port 2” columns), Fig. 2. You can enter an “X” for all the ports that need to be connected to the same segment as multiple transmission lines can be connected to it. Finally, close the Transmission Lines window.
- Select the second wire and repeat steps 1-4 to connect the second port of the transmission line to another segment, Fig. 3. The transmission lines with both ports connected will be graphically displayed as shown in Fig. 4.
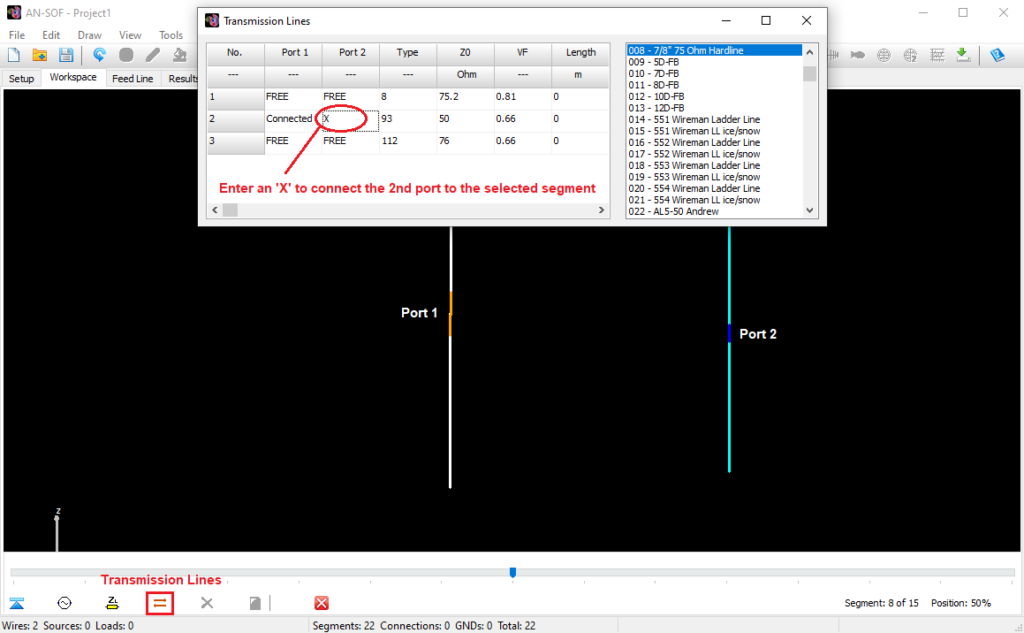
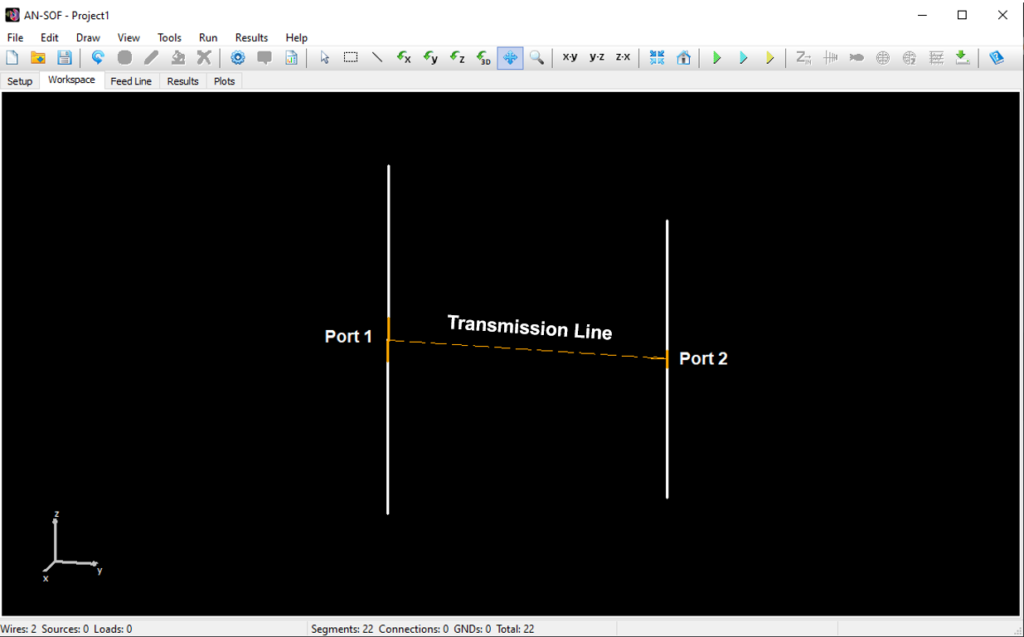
While performing this procedure, you have the option to add more transmission lines directly in the “Transmission Lines” dialog window. This saves you from having to follow the steps outlined in Adding Transmission Lines. The advantage of adding transmission lines here is that you can edit the connections of the lines in the “Port 1” and “Port 2” columns. However, with the Draw > Transmission Lines (Ctrl + L) command, you can quickly edit the lines (Z0, VF, length, etc.) if you don’t need to change the port connections.
A port that is already connected to a segment will show the status as “Connected,” while if it is not connected to any segment, it will display the status as “FREE”. When we are on a selected segment, a connected port will show the status as “Here,” which refers to the port being connected specifically to that selected segment.
To disconnect a port from a segment, enter the word “FREE” (without quotes, in uppercase) in the corresponding cell instead of an “X”. This allows you to use the “X” and “FREE” commands to easily connect and disconnect ports on a selected segment.
The transmission lines that have both ports connected to segments are displayed as straight dashed lines in orange color in the workspace, Fig. 4. An arrow will indicate the direction of the line, which goes from port 1 to 2. Since the length of a line is another parameter that is entered, such as its characteristic impedance and velocity factor, the length of the line in the workspace may not represent the configured or “real” length of the line.
If you select a row by clicking on the row number in the Transmission Lines table, the corresponding line will be highlighted in red in the workspace (if it has both ports connected to segments), Fig. 5. This way, you can visually identify which line you are editing.
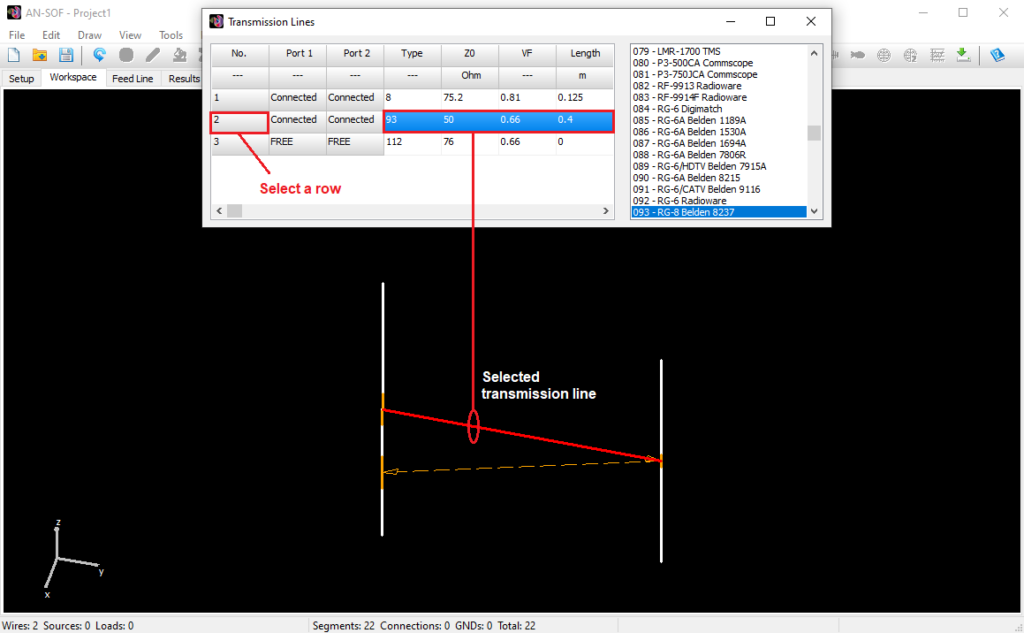
IMPORTANT Information
- A transmission line with only one port connected to a wire segment will not be considered in the calculations. Instead, it exists as a row within the table, which can be used as a library of lines to select from and connect to the wire structure. Therefore, when a port is FREE, it does not mean that the corresponding end of the transmission line is open circuited, but rather that this line will simply be omitted in the simulation. It is sufficient for only one port to be FREE for the line to be omitted. If you need to connect a line with an open or short-circuited end, please refer to Open and Short-Circuited Lines for detailed instructions.
- A voltage or current source can be connected to any segment where one or more transmission line ports are connected. In this case, the sources will always be “ideal”, i.e., with zero/infinite internal impedance (zero for voltage sources and infinite for current sources), unlike in an ordinary segment without a port connected, where sources may have non-zero/finite internal impedance (in AN-SOF, current sources should always have a finite internal impedance because this impedance is connected in parallel with the current source).
- In each segment, only transmission line ports or a load impedance are allowed, but not both. If a port is connected to a segment where a load impedance already exists, this impedance will be eliminated, and vice versa. If you need to connect a load impedance in series with the port of a transmission line, connect the impedance in an adjacent segment to the port.
- When there are transmission lines in the model, the NGF (Numerical Green’s Function) option will be automatically enabled in the Settings panel of the Setup tabsheet. This way, calculations will be performed faster in the next simulation if only the parameters of the transmission lines are modified while the wire structure remains unchanged.
- It is recommended to connect transmission lines after drawing and segmenting the wire structure. If the number of segments changes, the lines may become disconnected and need to be manually reconnected using the procedure described in this section.
- To ensure a smooth calculation process, AN-SOF will verify the correct connections between the transmission lines and the wire segments. If AN-SOF detects any errors, it will promptly remove the faulty connection by setting the corresponding port to FREE state.
Due to the model used in the calculation engine, the transmission lines that are considered to exist in the simulation are those that have both ports connected to wire segments. Therefore, if you want to have an open-circuited line connected to a certain segment, the opposite port must also be connected to another wire segment. Create a short wire with only one segment that is no longer than 1% of the wavelength (its radius can be one-tenth of its length) and connect it to the open circuit transmission line port. This short wire should be disconnected from the rest of the structure, and the shunt admittance of the port it’s connected to should be zero, Fig. 1.

On the other hand, if you need a transmission line with a short-circuited port, connect that port to any other segment and set a shunt admittance at that end that is very large, for example, 1E6 [S]. At this end, you could connect a short wire segment created for this purpose, as is done for an open-circuited line, Fig. 2.
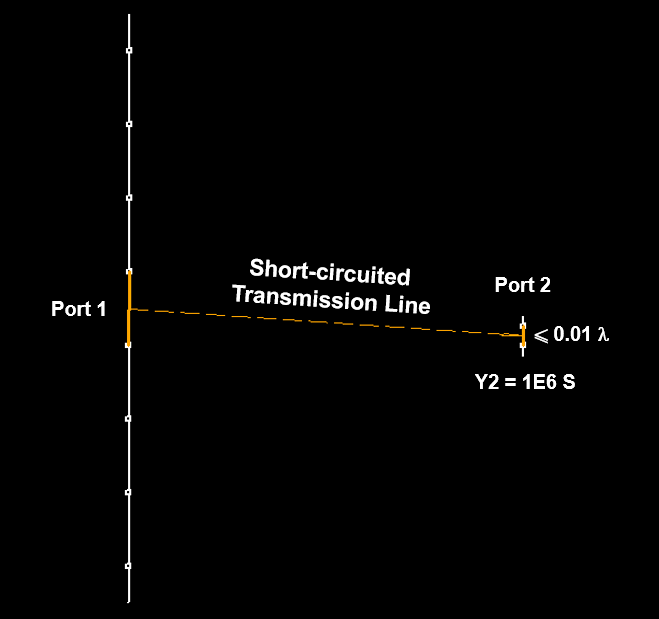
When creating short wires to connect open or short circuit transmission line ports, it is advisable to move these wires away from the rest of the structure to minimize interaction with it. Enter the length of the transmission line as indicated in Adding Transmission Lines. Remember that the length of the line is not necessarily related to the actual distance between the segments where it is connected.
The Transmission Lines table has a pop-up menu with keyboard shortcuts, Fig. 1. To access this menu for editing cells and rows, right-click on the table. The available commands are:
- Standard Cut (Ctrl + X), Copy (Ctrl + C), and Paste (Ctrl + V) options are available for cells. A single cell can be selected by left clicking on it or by using the TAB and arrow keys on the keyboard.
- To select a row, click on the row number in the left column (the “No.” column). Use the mouse or the up and down arrow keys on the keyboard to select a single row. Double-click on a single cell to exit row selection mode.
- Cut (Ctrl + X), Copy (Ctrl + C), and Paste (Ctrl + V) options also apply to a selected row. In addition, Insert (Ins key) and Delete (Del key) options can be used to add or remove rows.
- The Clear Contents (Ctrl + Del) command clears the content of a selected cell or row.
- The Move Rows (Ctrl + M) command allows you to enter a mode where rows can be moved up or down to order them as desired. To exit this mode, click Move Rows (Ctrl + M) again.
- The Update Ports (Ctrl + U) command checks and updates the status of the transmission line ports. Use this command to verify that the lines have their ports connected to wire segments when you have made any modifications to the segmentation or geometry of the wires where there are transmission line ports.
Coaxial transmission lines can be modeled implicitly, as explained in previous articles. To define a coaxial cable, one needs to know its characteristic impedance (Z0), velocity factor (VF), length, parameters that model losses (K0, K1, K2, etc.), and the shunt admittances at each end (Y1 and Y2). Additionally, each end or port of the line must be connected to the center of a wire segment. In this implicit model, the electromagnetic interaction between the coaxial cable shield and the wire structure is neglected, and the line ends impose boundary conditions on the voltage and current in the connected segments. However, in certain scenarios, a current can be induced that flows through the outside of the coaxial cable shield, known as common-mode current, and this current cannot be neglected. To address this, a hybrid model is used, which is explained in detail below.
In the hybrid model, the internal behavior of a coaxial cable is implicitly modeled using its parameters such as Z0, VF, length, etc. On the other hand, the outer shield is modeled by adding a wire that must be divided into segments like the rest of the structure, Fig. 1. This additional wire considers the current induced outside the coaxial cable shield.
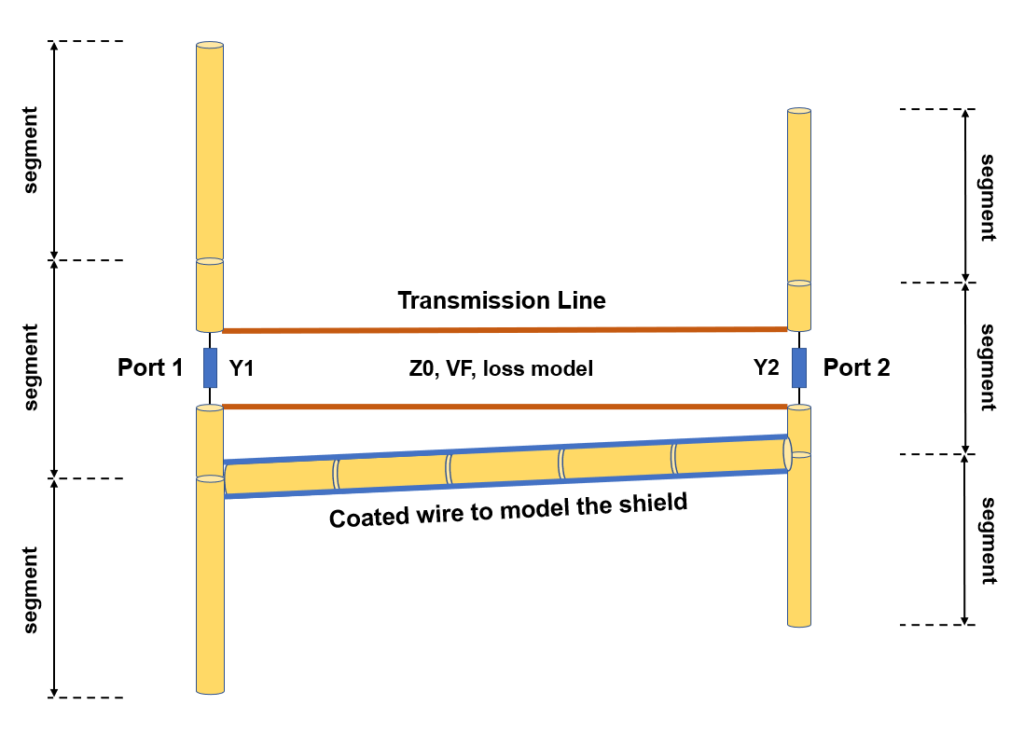
The wire representing the shield should be connected between two ends of the segments where the cable is connected, Fig. 2. Unlike transmission lines that connect in the center of the segments, wires are connected at their ends. Hence, the additional wire representing the shield will be a segment offset from the actual position of the cable. This is not a significant concern since the segments should be small compared to the wavelength.
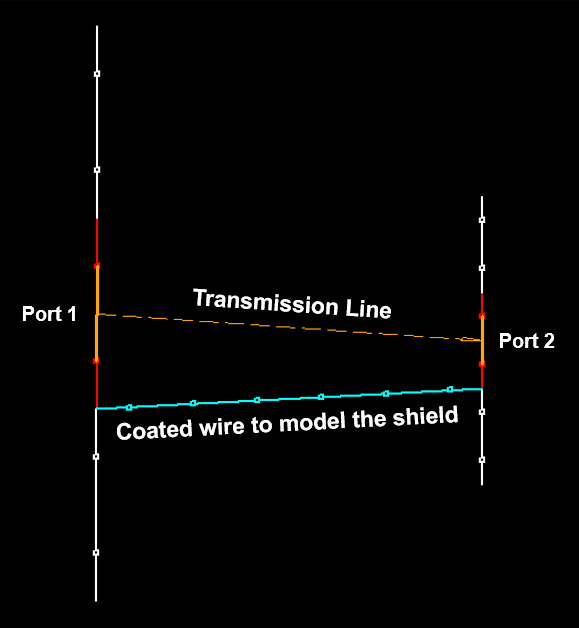
Please be reminded that to connect one wire to another and connect the ends of the coaxial cable shield, you will need to manually divide the wires involved, as explained in Connecting Wires.
To simulate the dielectric coating of actual coaxial cables, an outer insulation can be added to the wire representing the shield, and its thickness can be input as well.
AN-SOF provides parameters for modeling the losses of more than 160 types of transmission lines. These parameters have been obtained by adjusting the loss model to the attenuation curves published by manufacturers. In case a particular type of cable is not listed or if the manufacturer has updated the parameters, a custom transmission line can be created using the following procedure:
- Open the Transmission Lines window by going to the main menu > Draw > Transmission Lines (Ctrl + L) or follow the procedure in Connecting Transmission Lines to open this window by selecting a wire.
- Select a row from the table by clicking on the row number (under the first column labeled No.).
- In the panel on the right, double-click the Custom line low loss model option.
- All manufacturers publish the nominal characteristic impedance, Z0, and the velocity factor, VF. Enter these values as well as the length of the line. If you enter “0” in the length cell, the linear distance between the ends of the cable will be calculated.
- Manufacturers also publish an attenuation table as a function of frequency. Here is an example for the Belden 8237 cable, type RG-8/U:
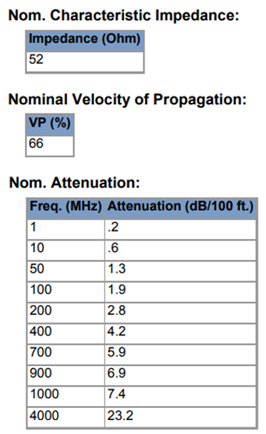
- In the cells corresponding to Att. 1, Freq. 1, Att. 2, and Freq. 2, enter the values from the attenuation table so that the simulation frequency range is included between Freq. 1 and Freq. 2. For example, if you are running a calculation between 150 and 170 MHz, enter Att. 1 = 1.9 dB/100 ft, Freq. 1 = 100 MHz, Att. 2 = 2.8 dB/100 ft, Freq. 2 = 200 MHz, as indicated in the table for the Belden 8237 cable, Fig. 1.
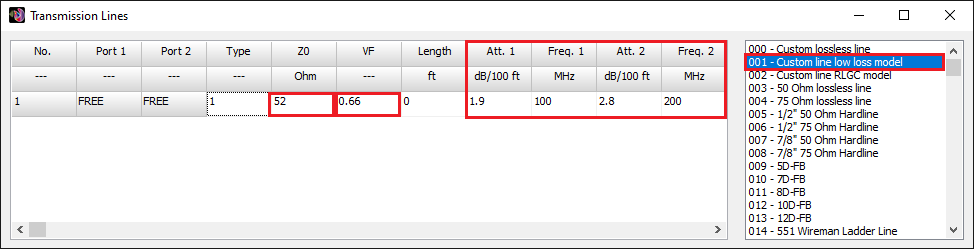
Be careful with the units of attenuation and frequency, as they will be displayed in the units chosen in the Preferences window. Go to main menu > Tools > Preferences > Units tab to change the units for frequency and length.
Step By Step
In the directory where AN-SOF was installed there is a folder called “Examples” which contains many examples of antennas and wire structures. The default directory is
C:\AN-SOF X\Examples
where X is the AN-SOF version.
You can also download the examples from here >.
We constantly upload files with examples on our website. You will find downloadable examples on our Resources and Blog pages.
At the bottom of our website there are Categories and a Search bar to facilitate the search for information.
We also invite you to subscribe to our Newsletter here > and to follow us on our social media channels.
From this link you can download 5 examples of antenna models that have less than 50 segments, so the calculations can be run with the trial version of AN-SOF:
- 2 Element Quad
- 2 Element Delta Loop
- HF Skeleton Slot
- Inverted V
- 5 Element Yagi-Uda
Discover 5 antenna models with less than 50 segments in AN-SOF Trial Version. These examples showcase the capabilities of our software for antenna modeling and design, allowing you to evaluate its features for your projects.
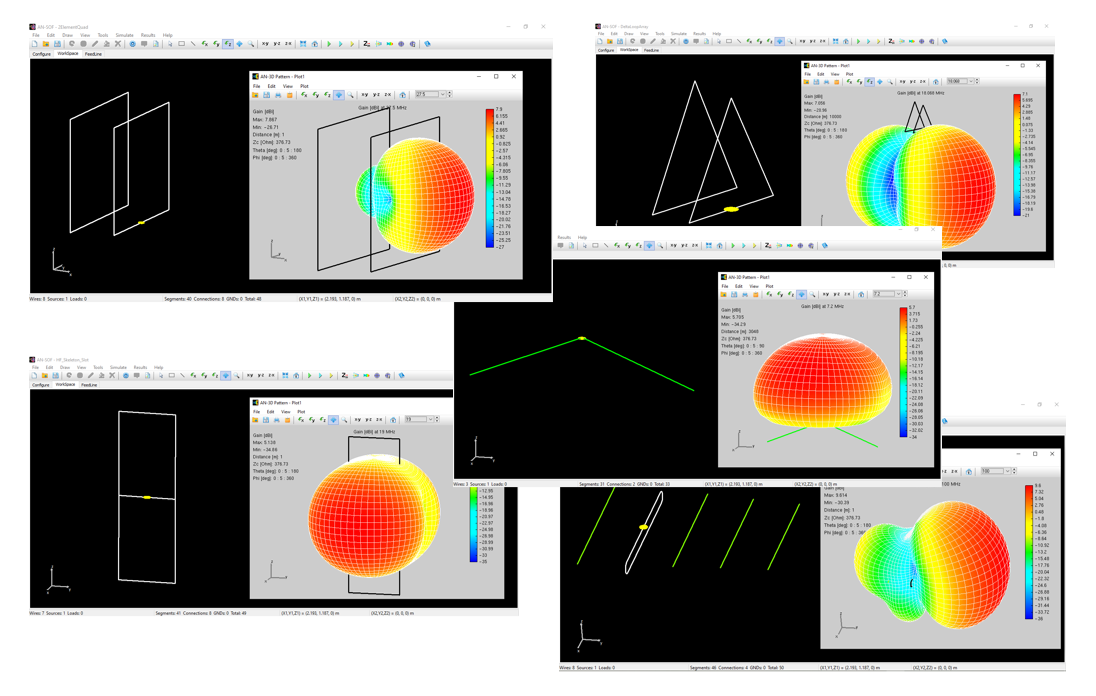
The trial version of AN-SOF is fully-featured and never expires. It allows users to open all pre-calculated example files to view tables and display various graphs and plots. The only limitation is that it can run calculations with up to 50 “unknowns”. An unknown refers to the electric current value to be determined by the AN-SOF calculation engine in each segment, segment-to-segment connection, and a connection to a ground plane, if any. Therefore, the total number of unknown currents equals the number of segments + number of connections + number of connections to ground. This number must not exceed 50 to run a calculation in AN-SOF Trial version.
The purpose of the trial version is to evaluate the AN-SOF features and capabilities for antenna modeling or design projects. The pre-calculated models can be found in the AN-SOF “Examples” folder typically located in the installation directory, such as C:\AN-SOF X\Examples, where “X” represents the version of the program. Additionally, many model examples with descriptive articles can be found in the Models section of our Knowledge Base. These models are categorized according to the antenna type, ranging from simple wire antennas to antennas in complex environments.
For more complex antennas, the 50 unknowns limit may be quickly exceeded. Modifications to pre-calculated examples with more than 50 segments + connections + ground connections cannot be re-run with the trial version of AN-SOF. However, for simple antenna projects or small antenna sizes in terms of the wavelength, the trial version can be a useful tool for simulations.
Download the following 5 examples with less than 50 segments to make modifications to the antenna structures:
- 2 Element Quad
- 2 Element Delta Loop
- HF Skeleton Slot
- Inverted V
- 5 Element Yagi-Uda
To achieve reliable results, at least 10 segments per wavelength of wire should be used in a model. For antennas sensitive to element lengths, like Yagis, about 50 segments per wavelength should provide results comparable to VSWR measurements.
Explore more examples and articles in the Validation section of our Knowledge Base. Additionally, AN-SOF trial version includes embedded tuner and feeder calculators, allowing users to synthesize impedance matching networks, add transformers, and calculate tuner and feed line parameters for measured or given load impedance.
In conclusion, AN-SOF Trial Version offers a comprehensive platform for antenna simulation, enabling users to evaluate its features and capabilities for their projects. With access to pre-calculated examples and embedded tools like tuner and feeder calculators, users can explore antenna designs with ease.
See Also:

About the Author
Tony Golden
Have a question?
Learn how to simulate a center-fed cylindrical antenna using AN-SOF software. This step-by-step guide covers setup, geometry creation, simulation, and result analysis. Understand dipole characteristics through practical examples.
Introduction: Center-Fed Cylindrical Antenna Simulation
The center-fed cylindrical antenna serves as a fundamental example for simulation. Essentially a straight wire with a central excitation, it transitions into a half-wave dipole when its length aligns with half the wavelength of the operating frequency. The following steps outline the simulation process using AN-SOF.
Step 1: Configuring the Simulation Environment
To initiate, navigate to Tools > Preferences within the main menu to establish appropriate units for frequency (MHz) and length (m). Subsequently, access the Setup tab. Within the Frequency panel, select Sweep and configure the Frequency Sweep parameters as depicted in Fig. 1. The calculations will be performed at the frequencies: 50, 55, …, 295, 300 MHz. Ensure that None (free space) is chosen in the Environment panel‘s Ground Plane box and Discrete Sources is selected under the Excitation panel.
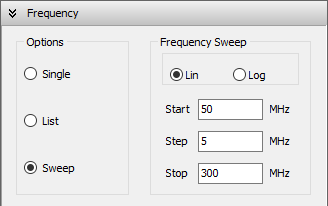
Step 2: Creating the Antenna Geometry
To initiate the antenna geometry creation, right-click within the workspace and select Line from the ensuing pop-up menu. The ‘Line’ dialog box will appear. Populate the Line and Attributes pages as outlined in Figs. 2 and 3 to generate a straight wire comprising 17 segments and a 1 mm radius within the workspace. The wire will be drawn starting from point (0,0,-0.75) [m] and ending at point (0,0,0.75) [m], aligning with the z-axis and spanning a length of 1.5 m, equivalent to a half-wavelength at 100 MHz. Press F7 to visualize the primary axes.
Subsequently, right-click on the wire and choose Source/Load/TL from the context menu. Following the procedure detailed in “Adding Sources,” introduce a voltage source at the wire’s center (segment 9). Set the source voltage to 1 (0°) V. The resulting center-fed cylindrical antenna in the AN-SOF’s workspace is represented in Fig. 4.
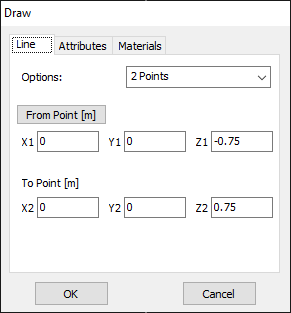
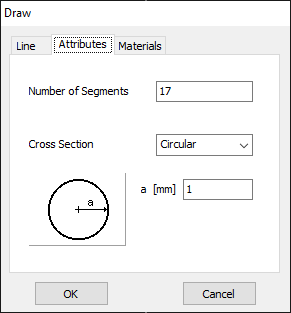
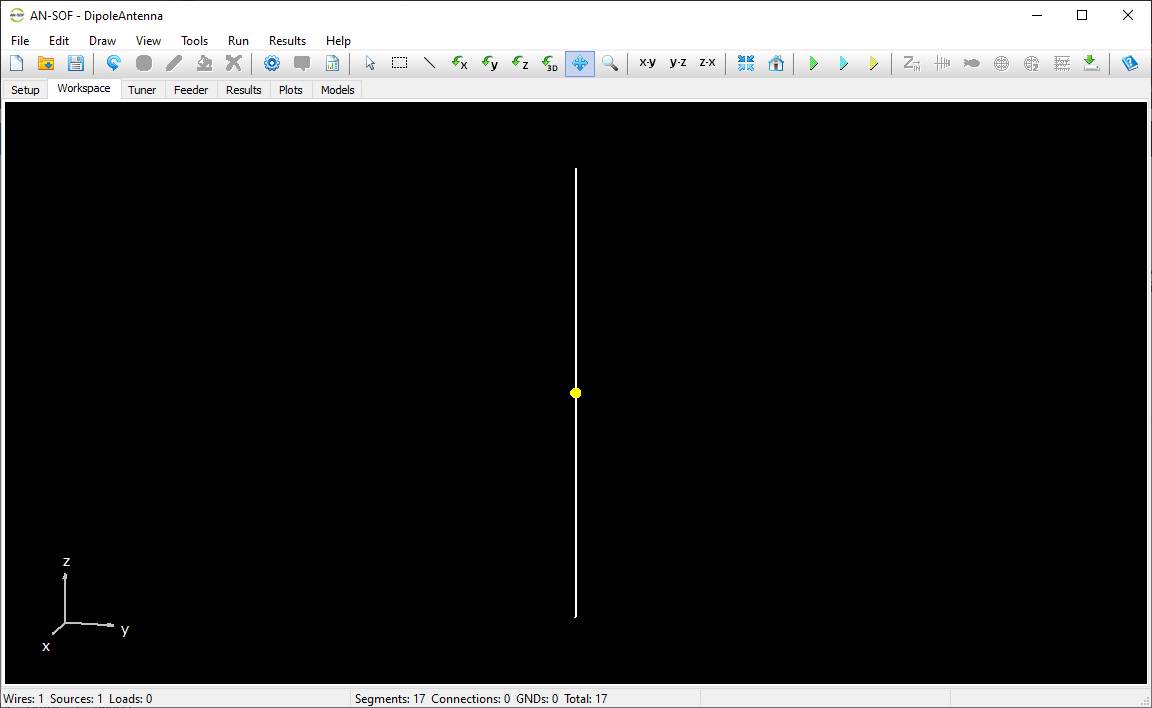
Step 3: Simulation Execution and Result Analysis
To initiate the simulation process, click the Run Currents and Far-Field (F11) button on the toolbar. Upon completion, right-click on the wire and select Plot Currents from the context menu, specifying the desired frequency. The resulting current distribution along the wire is graphically represented in Fig. 5. To access additional parameters of interest, refer to the procedures outlined in “Displaying Results.”
As an illustrative example, Figures 5, 6, and 7 depict the current distribution at 100 MHz (amplitude in Fig. 5(a) and phase in Fig. 5(b)), input impedance versus frequency (real part in Fig. 6(a) and imaginary part in Fig. 6(b)), and gain pattern in dBi (Fig. 7) at 100 MHz.
Given that the antenna length (1.5 m) equals half a wavelength at 100 MHz, the current distribution in amplitude approximates a half-cycle sine function, aligning with the expected behavior of a half-wave dipole. A slight decrease in the amplitude and a sharp increase in the phase can be seen at the antenna center, due to the presence of the voltage source just there. The presence of the voltage source at the center disrupts the continuity of the current’s slope (derivative) at that point, while the current itself remains continuous.
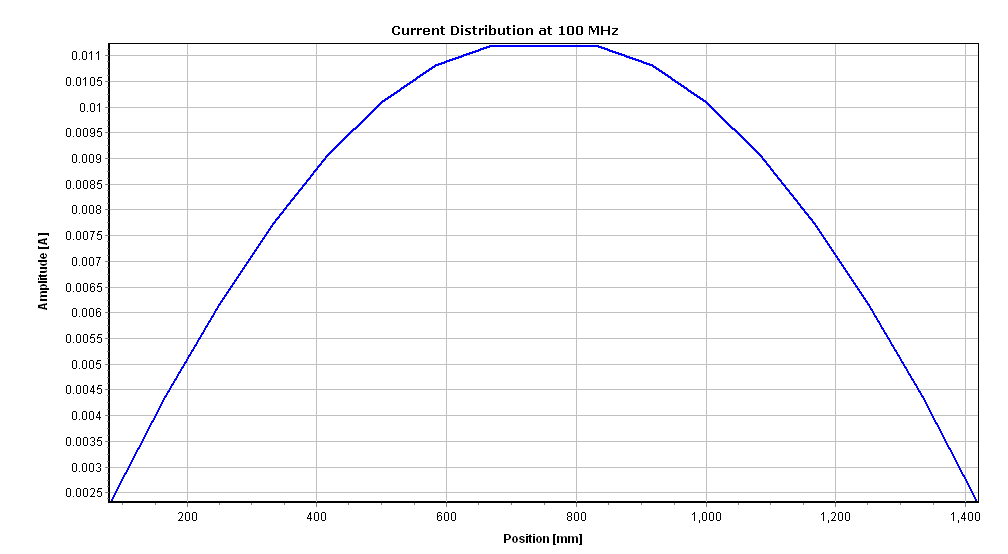
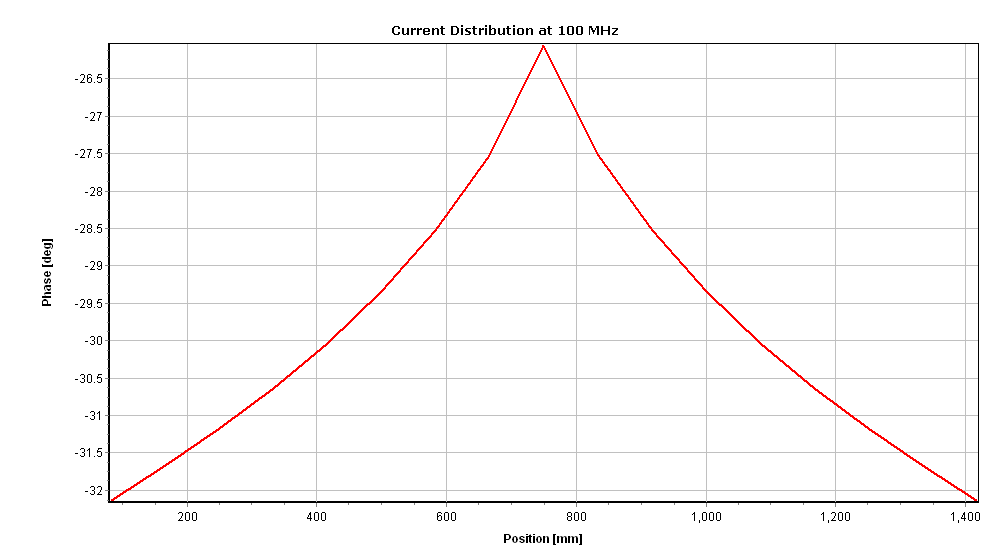
If we look closely at Figure 6(b), which shows the input reactance (imaginary part of the input impedance), we can see that the curve crosses zero just before 100 MHz, with a positive slope (series resonance), then crosses zero again just above 180 MHz, with a negative slope (parallel resonance), and then crosses zero again just below 300 MHz with a positive slope (series resonance). These three points where the reactance vanishes correspond to when the physical length of the dipole approaches: λ/2, λ, and 3λ/2. The resonances do not occur exactly at integer values of half wavelength because the thickness of the dipole is not infinitesimal. In Figure 6(a) we can see that the input resistance is maximum at the frequency that corresponds to the parallel resonance. All these are the expected and classical behaviors of a dipole of finite thickness.
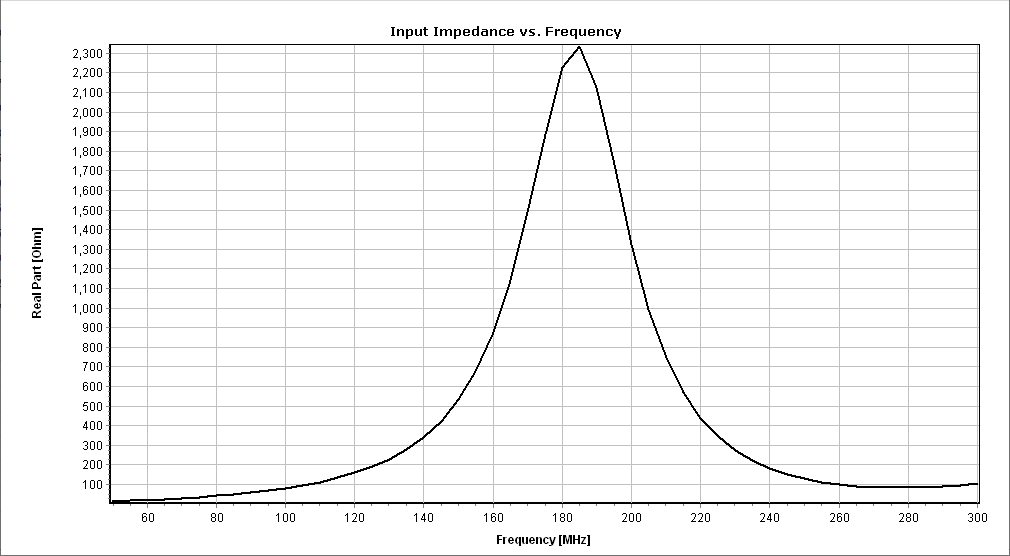
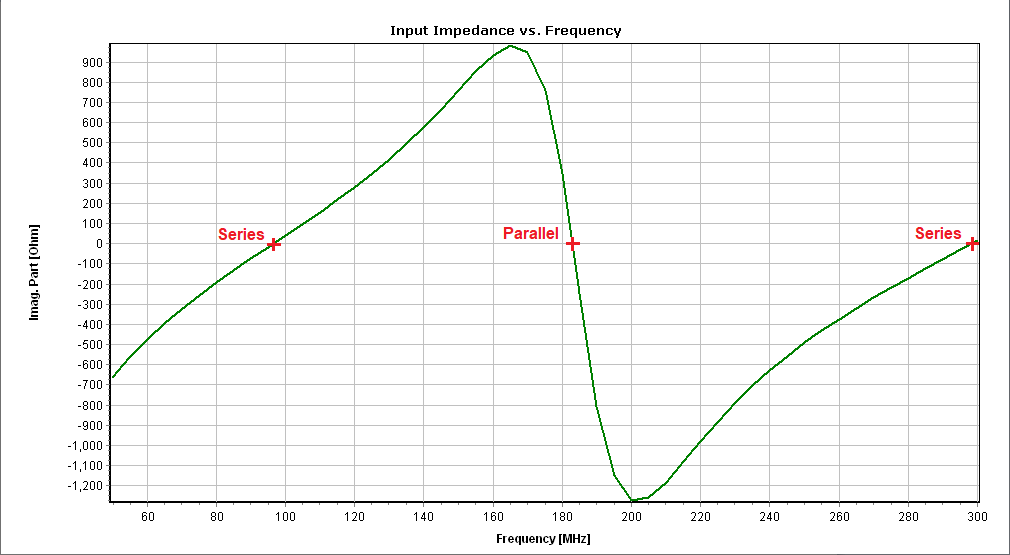
Regarding the gain pattern in Fig. 7, it is donut-shaped as expected for a half-wave dipole, with a maximum of 2.17 dBi. We should remember that the theoretical peak gain of an infinitesimally thin half-wave dipole in free space with a perfect sinusoidal current distribution is 2.15 dBi (corresponding to a numerical gain of 1.64). The obtained gain in AN-SOF is 0.02 dBi higher than the theoretical value due to the finite radius of the cross-section of the dipole.
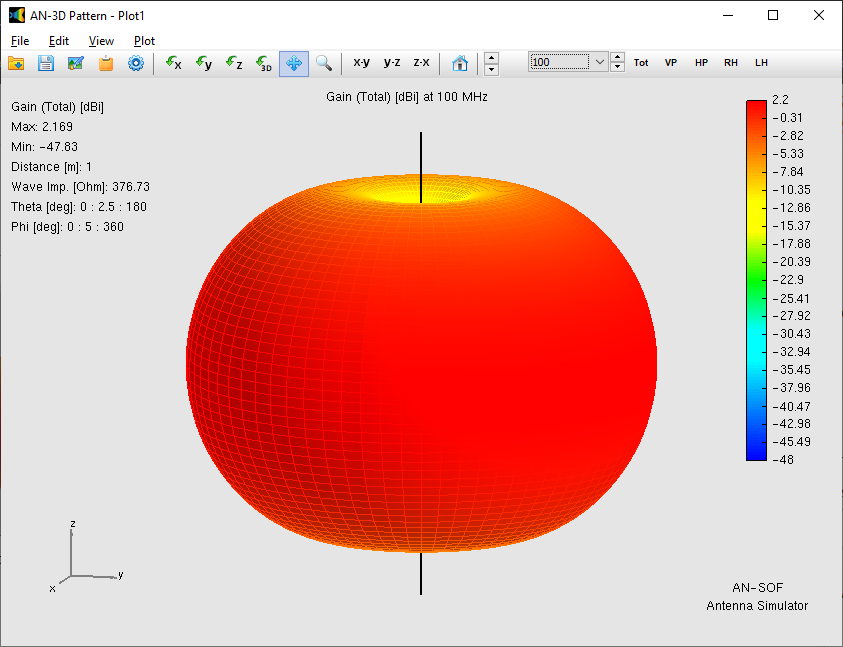
Conclusion
This tutorial provided a step-by-step guide to simulating a center-fed cylindrical antenna using AN-SOF Antenna Simulator. By following the outlined procedures, users can efficiently model this fundamental antenna type and analyze its key characteristics.
The simulated results align with the expected behavior of a half-wave dipole, demonstrating the software’s accuracy in predicting current distribution, input impedance, gain, and radiation patterns. The influence of the antenna’s finite thickness on the resonance frequencies and gain was also highlighted.
This example serves as a foundation for more complex antenna designs. By understanding the simulation process for this simple geometry, users can apply similar principles to model and analyze a wide range of antenna structures.
See Also:

About the Author
Tony Golden
Have a question?
This step-by-step guide empowers you to simulate circular loop antennas in AN-SOF. We’ll configure the software, define loop geometry, and explore how its size relative to wavelength affects radiation patterns and input resistance. Gain valuable insights into this fundamental antenna type!
This article provides a step-by-step guide to modeling a circular loop antenna using AN-SOF software. Circular loops are a common antenna type, and their analysis requires curved segments within the simulation environment. The guide will detail the configuration process, including defining the loop geometry, setting up the frequency sweep, incorporating a voltage source, and analyzing the key parameters like radiation pattern and input resistance. This guide is valuable for RF engineers, ham radio enthusiasts, students, and antenna design professionals seeking to utilize AN-SOF for circular loop antenna simulations.
1. Specifying the Simulation Setup
This section outlines the initial setup steps required to model a circular loop antenna in AN-SOF. We’ll configure a frequency sweep to analyze the antenna’s behavior across a specified range.
Frequency Sweep:
- Navigate to the Setup tab and select Sweep within the Frequency panel.
- Choose Lin for a linear frequency sweep. This allows for evenly spaced data points across the desired range.
- Define the sweep parameters:
- Start frequency: 3 MHz
- Step: 1 MHz (adjust as needed based on desired resolution)
- Stop frequency: 30 MHz
These settings establish a linear sweep from 3 MHz to 30 MHz with 1 MHz increments between each data point (as shown in Fig. 1).
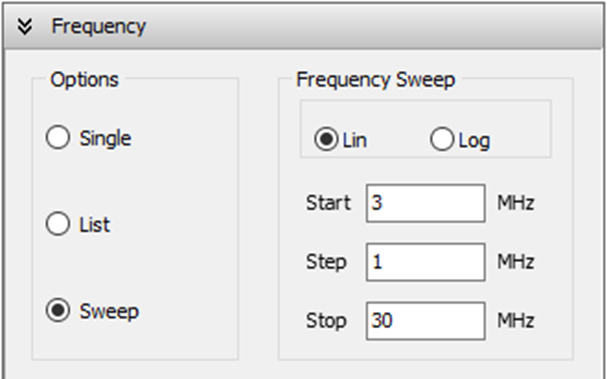
Additional Settings:
- Environment: Ensure that None is selected in the Ground Plane box within the Environment panel. This removes any ground plane influence from the simulation, which might not be relevant for a free-space loop antenna.
- Excitation: In the Excitation panel, verify that Discrete Sources is selected. This indicates that we’ll define a lumped source (voltage or current) to excite the antenna later in the modeling process.
By following these steps, we’ve established the foundation for our loop antenna simulation by configuring the frequency sweep and essential simulation settings in AN-SOF. The next section will delve into defining the geometry of the circular loop itself.
2. Defining the Circular Loop Geometry
This section focuses on creating the circular loop geometry within the AN-SOF workspace:
- Access the Draw Menu: Navigate to the Workspace tab. Right-click on an empty area within the workspace and select Circle from the pop-up menu.
- Specify Loop Parameters: The Draw dialog box for the circle will appear (Fig. 2). Define the following parameters for your loop antenna using the provided tabs:
- Center: (Cx, Cy, Cz) = (0, 0, 0) (Circle tab)
- Radius: 0.5 meters (Circle tab)
- Segments: 8 (Attributes tab)
- Cross-section type: Circular (Attributes tab)
- Cross-section radius: 5 millimeters (Attributes tab)
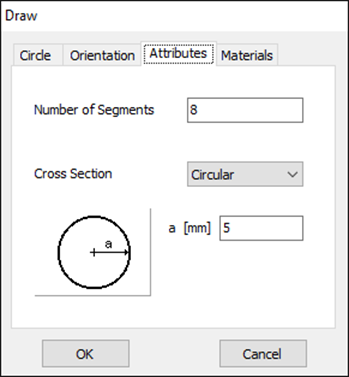
Segment Selection: The number of segments used to discretize the loop circumference is crucial for accurate simulation results. While 8 segments are a reasonable starting point, a convergence study might be necessary to ensure sufficient accuracy, especially for electrically large loops. As a rule of thumb, aim for 10-20 segments per wavelength at the highest frequency of interest.
Electrical Size Considerations: It’s important to consider the loop’s electrical size relative to the wavelength. At 30 MHz (the highest frequency in your sweep), the wavelength (λ) is indeed 10 meters, and the loop’s circumference (0.314λ) is close to one-third of a wavelength. This suggests the loop might not be electrically small at the high end of the frequency range. This characteristic will affect the antenna input impedance and radiation pattern.
Assigning the Excitation Source:
- Right-click on the circular loop within the AN-SOF workspace.
- From the pop-up menu, select Source/Load.
- Choose to add a voltage source and position it at the first segment of the loop.
For detailed instructions on source placement and parameter definition, refer to the AN-SOF documentation’s ‘Adding Sources‘ section.
3. Running the Simulation and Analyzing Results
This section guides you through initiating the simulation process and analyzing the obtained results in AN-SOF:
- Run Simulation: Locate the Run Currents and Far-Field (F11) button on the toolbar and click it. This initiates the simulation, calculating the current distribution on the loop and its far-field radiation pattern across the defined frequency sweep.
- Visualizing the Radiation Pattern: Once the simulation is complete, click the Far-Field 3D Plot button on the toolbar. This will display the radiation pattern of the loop antenna in a 3D format (AN-3D Pattern application similar to Fig. 3).
- Frequency-Dependent Analysis: The AN-3D Pattern toolbar offers functionalities to explore the radiation pattern’s behavior at different frequencies within the sweep range.
- Frequency selection dropdown menu: This menu allows you to directly choose a specific frequency point to view its corresponding radiation pattern.
- Frequency navigation buttons: Utilize the up and down arrow buttons on the toolbar to navigate through the calculated frequencies and observe the dynamic changes in the radiation pattern. As expected for a circular loop antenna, the pattern should exhibit a doughnut-like shape at lower frequencies.
- Input Resistance Analysis: Navigate to the Results tab within AN-SOF. Here, you should observe a very low input resistance value, likely around 0.000195 Ohm at 3 MHz.
- Comparison with Theoretical Radiation Resistance: The well-known formula for the radiation resistance, Rr, of an electrically small loop antenna is Rr = 31,200 (A/λ2)2. Applying this formula with the loop’s area (A) and the wavelength (λ) at 3 MHz, you obtain a theoretical value of Rr ≈ 0.000192 Ohm. The close agreement between the simulated and theoretical values at 3 MHz demonstrates that the loop behaves according to the small loop antenna model at lower frequencies within the sweep range.
Important Note:
It’s important to remember that the formula used for radiation resistance applies to electrically small loops. As mentioned earlier, the chosen loop dimensions might not be electrically small across the entire frequency sweep (especially at 30 MHz). This will lead to deviations between the theoretical and simulated results at higher frequencies.
Figure 3 illustrates the frequency dependence of the loop antenna’s 3D radiation pattern. Subfigures (a), (b), and (c) depict the patterns at 3 MHz, 15 MHz, and 30 MHz, respectively.
By following these steps, you’ve successfully run the simulation, analyzed the radiation pattern, and compared the input resistance with theoretical expectations.
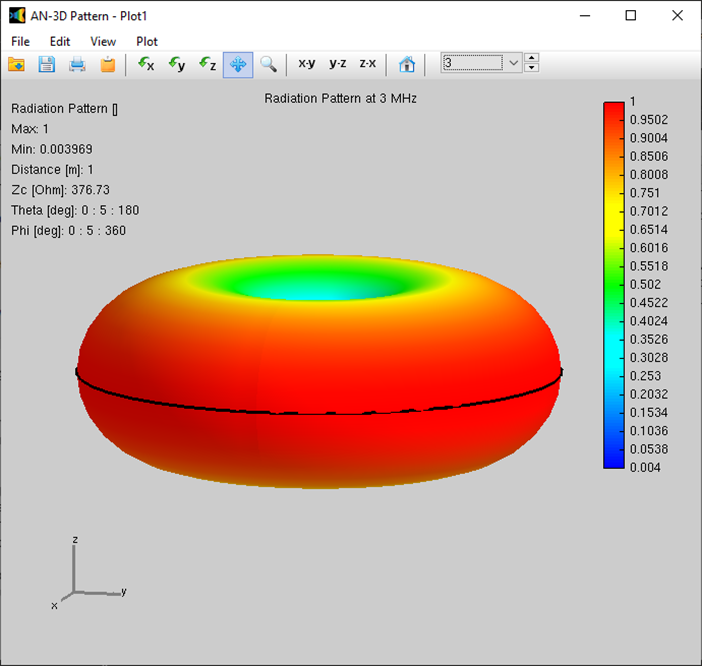

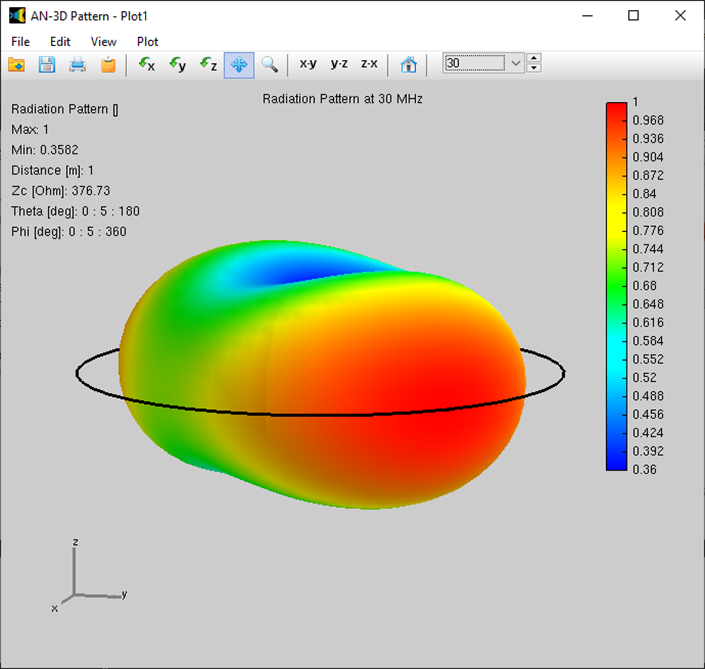
See Also:

About the Author
Tony Golden
Have a question?
Explore the design and simulation of monopole antennas over imperfect ground using AN-SOF. Learn how ground conditions impact performance and optimize efficiency for LF/MF broadcasting applications.
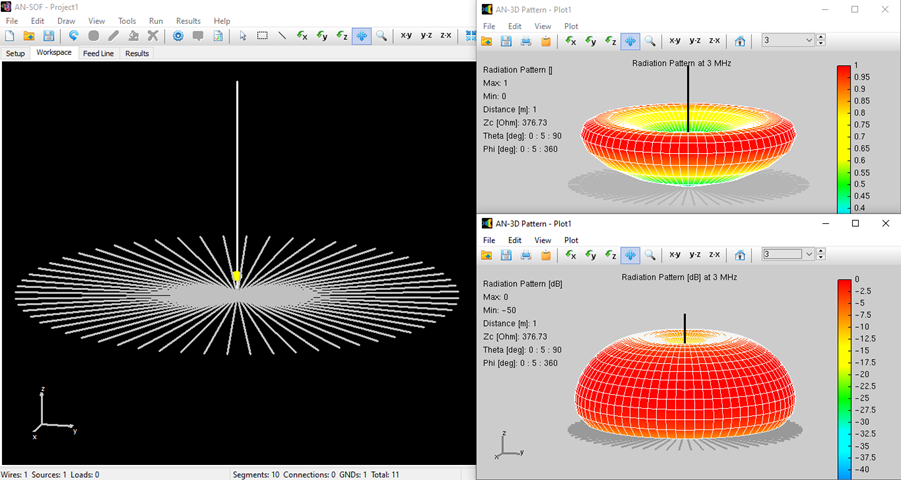
Introduction
A monopole antenna is a class of radio antenna consisting of a single radiating element, typically mounted vertically over a conductive ground plane. It is one of the simplest and most widely used antenna designs, particularly in applications where space and simplicity are critical. The monopole can be thought of as half of a dipole antenna: by introducing a ground plane, one of the dipole’s two radiating elements is effectively replaced by the ground plane’s mirror image, creating a virtual “second leg.” This results in a structure that is electrically equivalent to a dipole but requires only half the physical height, making monopoles particularly advantageous for low-frequency and compact installations.
Monopole antennas are commonly used in a variety of applications, including AM/FM broadcasting, LF (Low Frequency) and MF (Medium Frequency) communication systems, mobile and base station antennas, and amateur radio setups. Their omnidirectional radiation pattern in the horizontal plane makes them ideal for broadcasting and communication over wide areas. However, their performance is highly dependent on the quality of the ground plane, as losses in the ground can significantly reduce efficiency and gain.In this article, we will simulate a monopole antenna in the form of a radio mast operating over imperfect ground, typical of LF and MF broadcasting scenarios. We will explore the impact of ground conditions on antenna performance and demonstrate how to optimize the design for improved efficiency.
Step 1 | Setup
Navigate to the Setup tab and set the operating frequency to 3 MHz in the Frequency panel. Next, go to the Environment panel > Ground Plane box and select the Real option, as shown in Fig. 1. Choose the Radial wire ground screen and Poor ground options. Note that the soil conductivity will automatically be set to 0.001 S/m and the relative permittivity (dielectric constant) to 5.
Finally, configure the number of radials, their length, and their radius as illustrated in Fig. 1. For radio masts, it is common practice to use a constant input power as a reference, such as 1 kW. Proceed to the Excitation panel, select Discrete Sources, then choose Set Input Power and enter 1,000 W, as shown in Fig. 2.
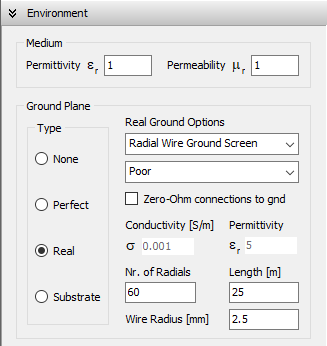
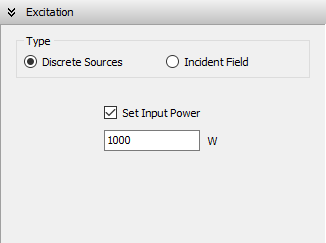
Step 2 | Draw
Right-click on the workspace and select Line from the pop-up menu. Specify a vertical wire with a height of 25 meters (equivalent to 1/4 wavelength at 3 MHz) and a triangular cross-section, as illustrated in Fig. 3. Although the recommended minimum number of segments is 3, we will divide the wire into 10 segments to achieve higher resolution in the current distribution. Note that the wire will automatically be connected to the ground at the origin (0, 0, 0).
Next, right-click on the wire and select the Source/Load command from the pop-up menu. Place a voltage source on the first segment to ensure the source is connected to the base of the mast. For further details, refer to the Adding Sources section.
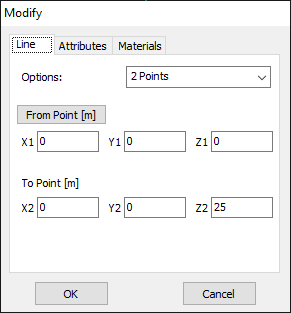
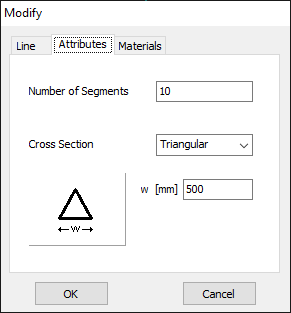
Step 3 | Run
Click on the Run Currents and Far-Field (F11) button located on the toolbar. Once the calculations are complete, click on the Far-Field 3D Plot button on the toolbar to display the radiation pattern. In the AN-3D Pattern window, select Radiation Pattern from the Plot menu to generate the normalized radiation pattern (dimensionless). Then, choose the Radiation Pattern [dB] option to view the pattern in decibel scale. Note that the far field exhibits a null on the xy-plane due to losses in the ground plane, as shown in Fig. 4.
The antenna efficiency is defined as the ratio of radiated power to input power. Navigate to the Results tab to view key parameters such as input impedance, VSWR, directivity, gain, and efficiency, as illustrated in Fig. 5. You will observe that the efficiency is relatively low, which consequently results in low gain, as a significant portion of the input power is dissipated in the ground. In this example, we have intentionally chosen a Poor soil condition. To improve antenna efficiency, experiment with different soil types, increase the number of radial wires, and adjust their lengths.


Conclusion
Simulating monopole antennas using the AN-SOF Antenna Simulator offers significant advantages for engineers and designers. By leveraging its advanced modeling capabilities, users can accurately predict antenna performance, optimize designs, and evaluate the impact of various ground conditions without the need for costly and time-consuming physical prototypes.
The ability to analyze parameters such as radiation patterns, input impedance, gain, and efficiency provides invaluable insights, enabling the development of high-performance monopole antennas tailored to specific applications.
Whether you’re designing for LF/MF broadcasting, mobile communications, or amateur radio, AN-SOF empowers you to explore design trade-offs and achieve optimal results with precision and efficiency.
See Also:

About the Author
Tony Golden
Have a question?
Perfect for Beginners: Quick Guide to Helix Antenna Simulation.
Master axial-mode helix design in AN-SOF with this easy step-by-step tutorial. Learn ground plane setup, helix creation, and radiation pattern analysis. Start modeling professional antennas today!
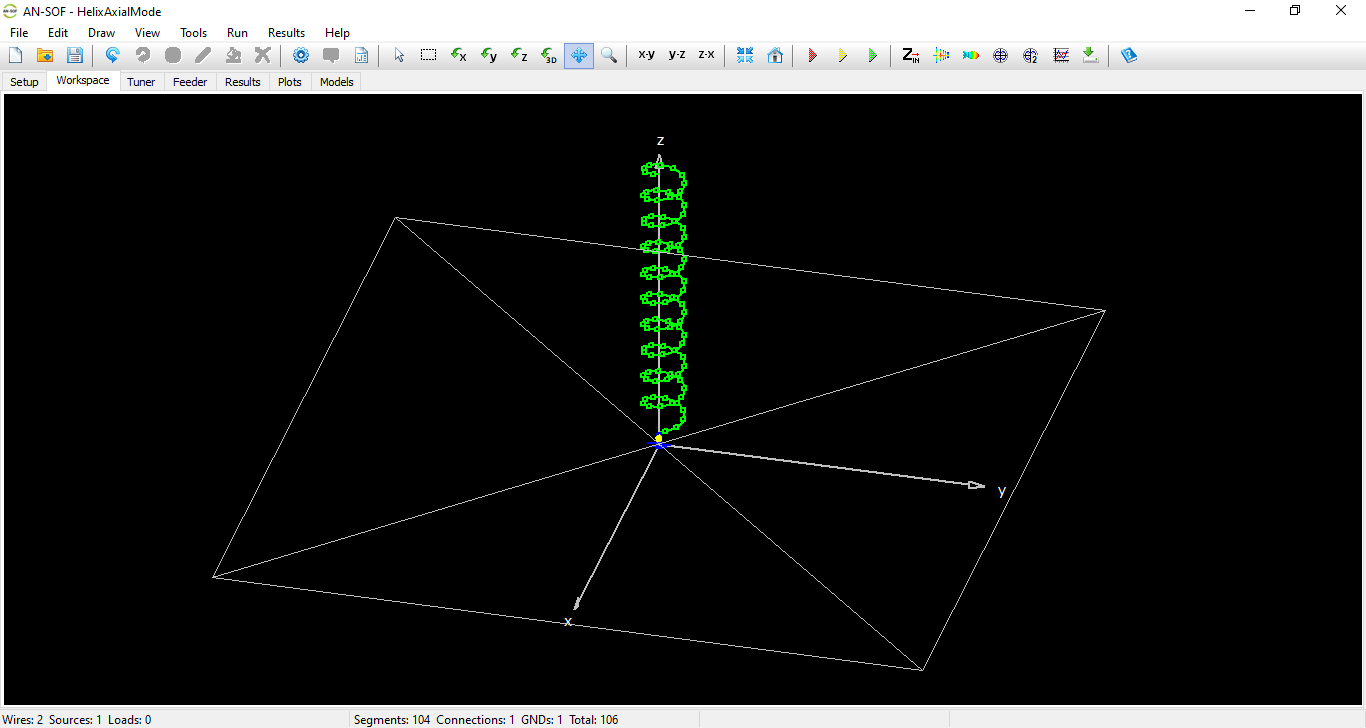
Helix Antenna in Axial Mode
The helix antenna demonstrates the importance of curved segments for accurate geometry representation. When the helix length approaches or exceeds the operating wavelength, it operates in axial mode – characterized by endfire radiation along its axis. This requires a ground plane reflector for proper operation.
Step 1: Setup
- Frequency Setup:
- Navigate to Setup tab > Frequency panel
- Set operating frequency: 100 MHz
- Ground Plane Configuration:
- Go to Environment panel > Ground Plane box
- Select: Perfect
- Set position: Z = 0 (xy-plane) (Fig. 1)
- Excitation:
- Ensure Discrete Sources is selected in Excitation panel
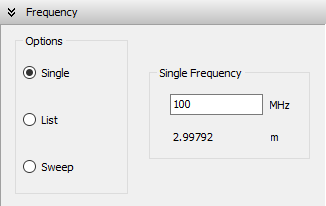
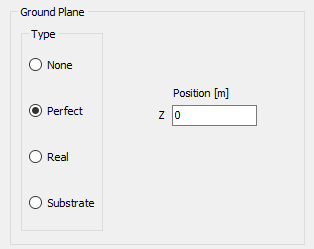
Step 2: Drawing the Structure
- Helix Creation:
- Right-click on the workspace > Select Helix from pop-up menu
- Draw Helix dialog appears (Fig. 2)
- Start point: (0, 0, 0.3) m (above ground plane)
- Orientation: Z-axis
- Axial Mode Dimensions:
- Set parameters per antenna textbooks:
- Radius
- Pitch (turn spacing)
- Number of turns (shown in Fig. 2)
- Attributes tab:
- Segments: 103 (recommended)
- Cross-section: Circular, radius = 3 mm
- Set parameters per antenna textbooks:
- Ground Connection:
- Right-click helix > Start Point to GND
- Draw Line dialog auto-populates connection points (Fig. 3)
- Set:
- Segments: 2
- Radius: 3 mm
- Source Placement:
- Right-click vertical wire > Source/Load/TL
- Connect voltage source to segment nearest ground plane
(Refer to: Adding Sources guide)
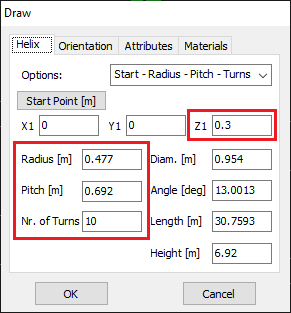
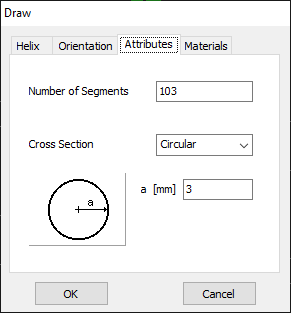
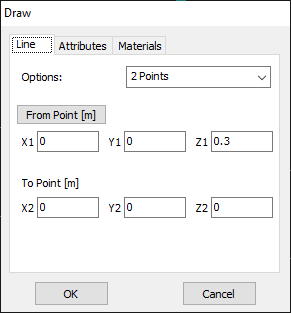
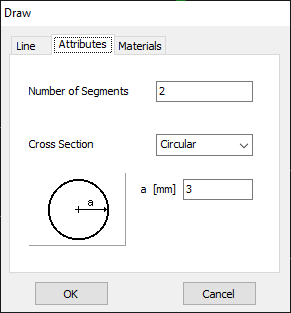
Step 3: Simulation & Analysis
- Run Simulation:
- Click Run Currents and Far-Field (F10)
- View 3D radiation pattern via Far-Field 3D Plot button (Fig. 4a)
- Observe main lobe along helix axis (axial mode characteristic)
- Polarization Analysis:
- In AN-3D Pattern Plot:
- Compare E-right vs. E-left components (Figs. 4b, 4c)
- For accurate comparison:
- Set matching scale maxima (Edit > Preferences)
- In AN-3D Pattern Plot:
- Left-Handed Variant:
- Create by specifying negative turn count
- Re-run simulation and compare polarization components
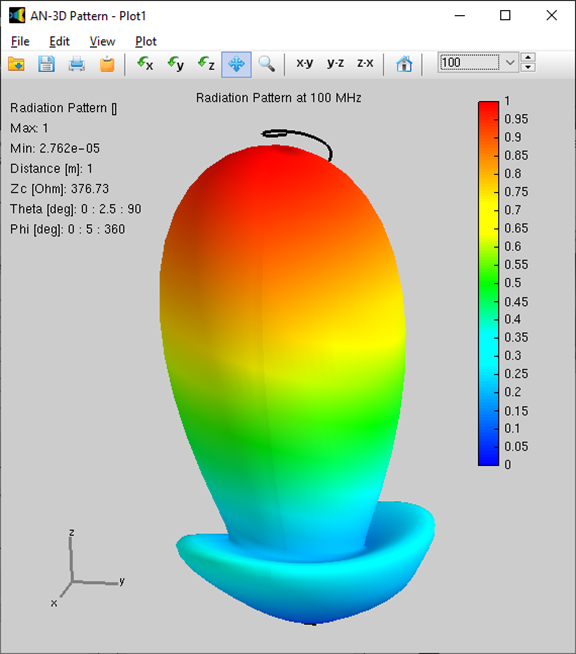
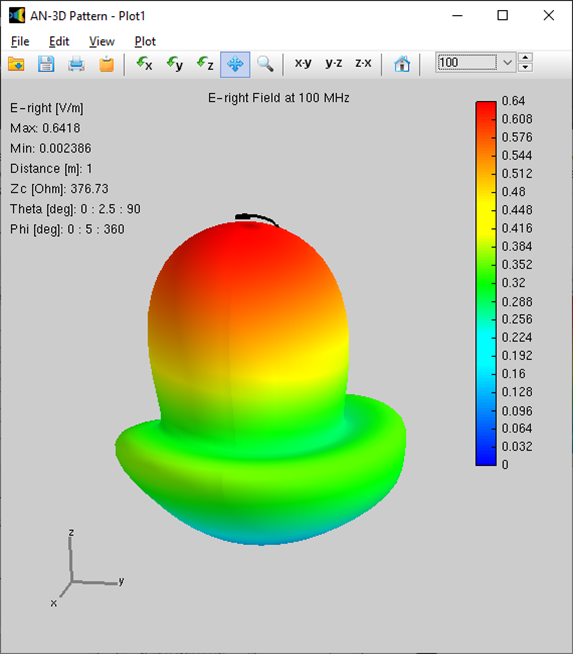
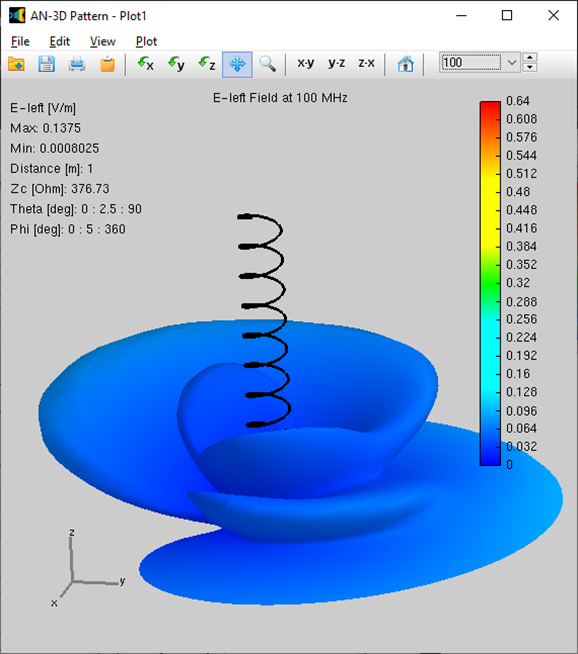
Key Features Demonstrated
- Curved segment modeling for helical structures
- Axial mode radiation characteristics
- Circular polarization analysis
- Ground plane integration
- Parametric comparison (right vs. left-handed)
The complete simulation showcases AN-SOF’s capability to model complex antenna behavior with precise geometrical control.
See Also:

About the Author
Tony Golden
Have a question?
Master Yagi-Uda simulation in AN-SOF! This quick guide walks you through modeling a 3-element array (reflector, driven element, director). Analyze radiation patterns with professional results.
Introduction to Yagi-Uda Antennas
The Yagi-Uda antenna, commonly called simply “Yagi,” is a directional antenna array developed in 1926 by Japanese researchers Hidetsugu Yagi and Shintaro Uda. This elegant design consists of three key elements:
- A driven element (typically dipole)
- Reflectors (usually 1-2 elements)
- Directors (multiple elements)
Through careful spacing of these elements, Yagis achieve high directivity and gain in one direction while being relatively simple to construct. They revolutionized radio communication and remain popular today for applications ranging from TV reception to amateur radio.
Yagi-Uda Simulation Basics
Now that you’ve mastered cylindrical antenna basics, let’s progress to antenna arrays. This guide walks you through simulating a classic 3-element Yagi-Uda design (Fig. 1) featuring:
- Director (front element)
- Reflector (rear element)
- Driven element (center dipole)
Step 1: Simulation Setup
- Frequency Configuration:
- Setup tabsheet > Frequency panel
- Set: 300 MHz (UHF range ideal for Yagis)
- Environment Settings:
- Environment panel > Ground Plane: Select None (standalone array)
- Excitation panel: Confirm Discrete Sources is active
Step 2: Building the Array
- Element Construction:
- Draw each wire individually (as in cylindrical antenna tutorial)
- Use coordinates from Fig. 1 for precise spacing
- Segment Configuration:
- Uniformly set for all elements:
- Segments: 15 (balanced accuracy/speed)
- Radius: 5 mm (typical for UHF)
- Uniformly set for all elements:
- Source Attachment:
- Right-click driven element > Source/Load/TL
- Connect voltage source to center segment
(Pro Tip: Middle placement ensures symmetrical excitation)
Step 3: Running & Analyzing
- Execute Simulation:
- Click Run Currents and Far-Field (F10)
- Observe 8.7 dBi peak gain in Results tab (Fig. 2)
- Radiation Pattern:
- Click Far-Field 3D Plot to visualize:
- Forward-directive beam (Fig. 3)
- Characteristic side/null patterns
- Click Far-Field 3D Plot to visualize:

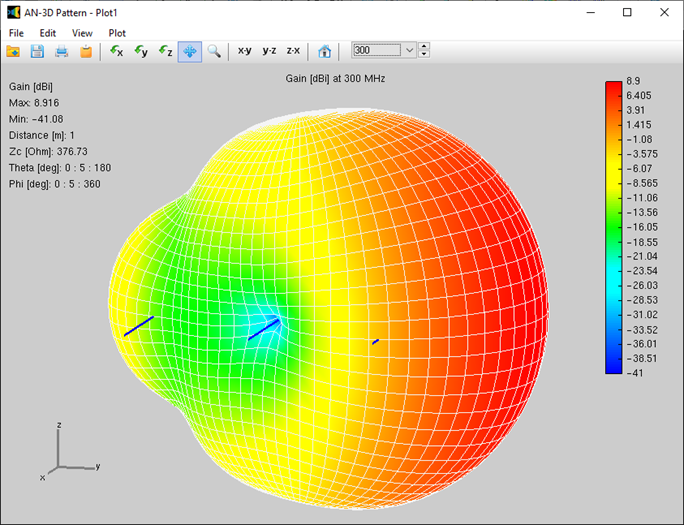
Why This Matters
- Teaches fundamental array principles
- Demonstrates directional gain enhancement
- Provides baseline for more complex designs
(Try modifying element spacing/numbers to see performance changes!)
See Also:

About the Author
Tony Golden
Have a question?
Two-wire transmission lines can be modeled explicitly in AN-SOF. In this example, the line will have a single wire but there will be a ground plane below it, so we have the mirror image of the wire as the return of the line.
Step 1 | Setup
Go to the Setup tab and select Single in the Frequency panel >. Set a frequency of 100 MHz. Then, go to the Environment panel > and set a perfect ground plane at Z = 0, Fig. 1.
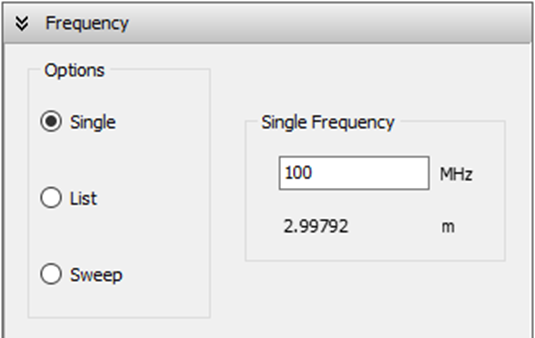
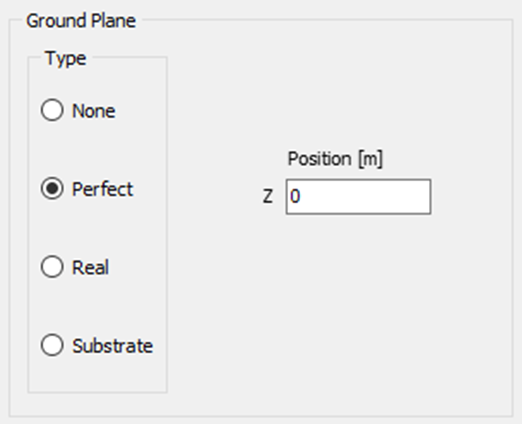
Step 2 | Draw
Go to the Workspace tab, right click on the screen, and select Line from the pop-up menu >. Draw a horizontal line with the coordinates indicated in Fig. 2. Next, connect the ends of the line to the ground plane by drawing two vertical wires. You can right click on the line and select the commands Start point to GND and End point to GND to connect the ends to ground.
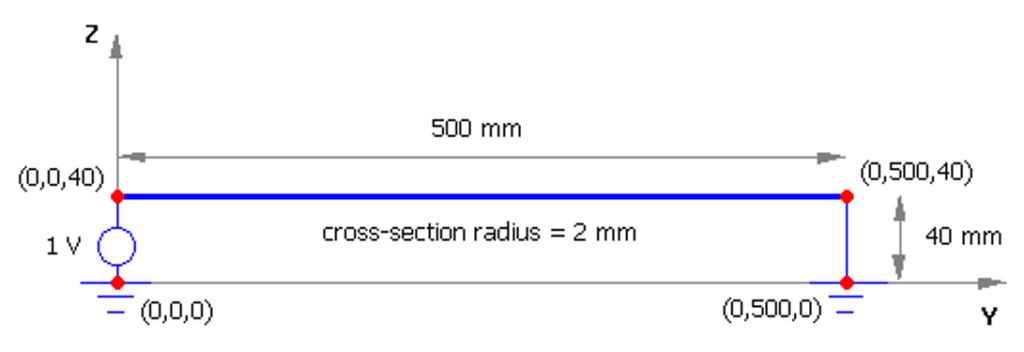
Set 40 segments for the horizontal wire and 1 segment for each of the vertical wires. Note that dimensions in Fig. 1 are in millimeters. To change the unit of length, go to Tools menu > Preferences > Units tab >.
Right click on the vertical wire at (0,0,0), select Source/Load from the displayed pop-up menu and put a 1 Volt voltage source on it. Refer to Adding Sources > to add the voltage source.
Step 3 | Run
Go to the Run menu and click on Run Currents. Since we are only interested in the current distribution and the input impedance, it is not necessary to calculate the radiated field (you can do it to check that it is practically negligible). Click on the Zin (List Input Impedances) button on the toolbar to display a table where the input impedance is shown as a function of frequency, Fig. 3. Refer to Listing Input Impedances >.
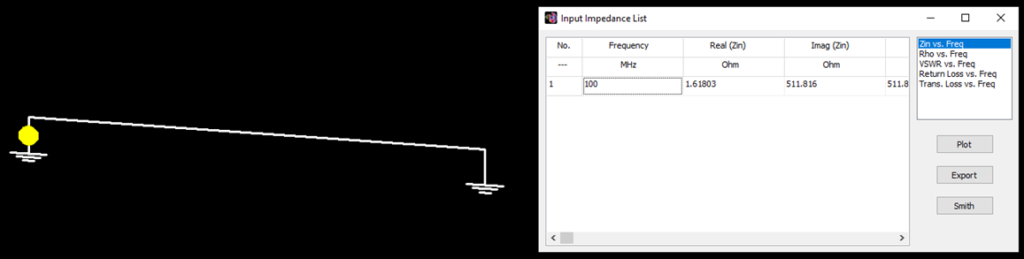
The impedance obtained is practically reactive, j512 Ohm. The small real part is the radiation resistance, since the line radiates a small amount of power, which is negligible but not zero.
This is a short-circuited line. Now right click on the vertical wire at (0,500,0) mm and select Delete from the pop-up menu to remove it. You will get an open-circuited line in this way. Rerun the calculations with the Run Currents command in the Run menu. The input impedance will now be -j105 Ohm.
Summarizing, we have,
- Zin (short-circuited line) = j512 Ohm.
- Zin (open-circuited line) = -j105 Ohm.
According to transmission line theory, the characteristic impedance can be calculated as the geometric mean of the short-circuit and open-circuit line input impedances, hence
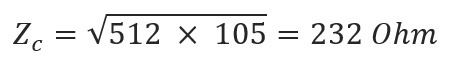
On the other hand, the expression for the characteristic impedance of a line above a ground plane is given by:
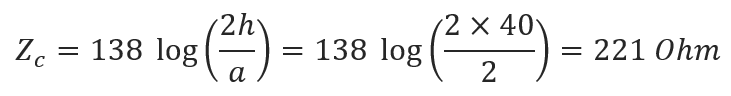
where a is the wire cross-section radius and h is the line height above the ground plane. As we can see, the agreement between the characteristic impedance obtained from AN-SOF and that from theory is quite good. The difference is since the theory neglects the radiation of the line, and the logarithmic formula is an approximation that is valid when h >> a.
The ability of AN-SOF to simulate at extremely low frequencies can be demonstrated with a model of an RLC circuit that will resonate at only 800 Hz, so the wavelength is 375 km!
Step 1 | Setup
Go to Tools > Preferences > in the main menu and select Hz, mm, mH and uF as the units for frequency, length, inductance, and capacitance, respectively. Then, go to the Setup tab and select Sweep in the Frequency panel >. Choose Lin for a linear sweep and set the Start, Step, and Stop frequencies. The frequency sweep will start at 600 Hz and end at 1,000 Hz, incrementing by 10 Hz for each calculation, Fig. 1. In the Environment panel >, set a perfect ground plane at Z = 0.
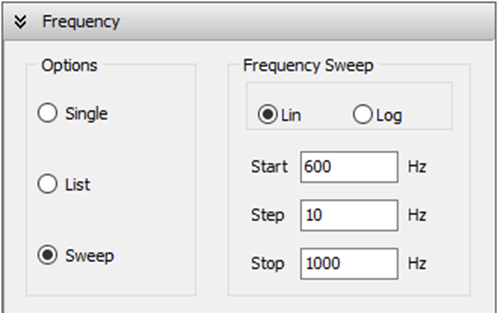
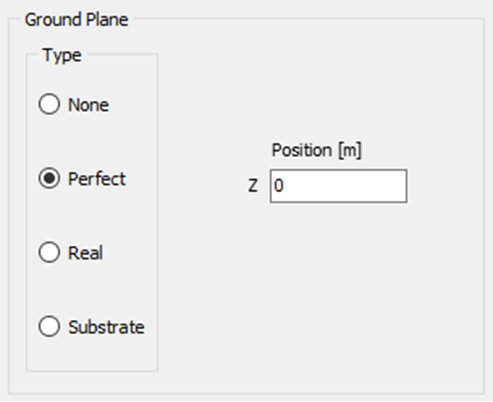
Step 2 | Draw
Go to the Workspace tab, right click on the screen, and select Line from the pop-up menu >. Draw the three wires with the coordinates indicated in Fig. 2 using the Line dialog box. The left vertical wire has 1 segment, the horizontal wire has 1 segment, and the right vertical wire has 2 segments. The wire radius is 0.5 mm.
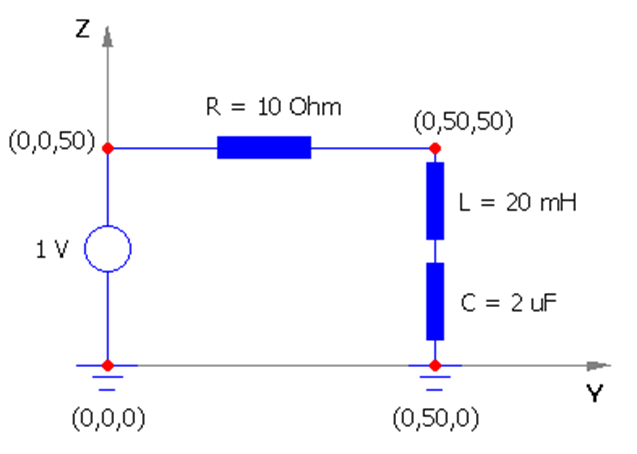
Right click on the left vertical wire, select the Source/Load command from the pop-up menu and put a 1 Volt voltage source. Then, right click on the horizontal wire, select Source/Load from the pop-up menu and connect a load impedance with R = 10 Ohm. Finally, right click on the right vertical wire, select Source/Load from then pop-up menu and put an inductance L = 20 mH on the first segment and a capacitance C = 2 uF on the second segment. Refer to Adding Sources > and Adding Loads > for adding sources and load impedances.
Step 3 | Run
Go to the Run menu and click on the Run Currents command. Since we are only interested in the input impedance, it is not necessary to calculate the radiated field (you can do it to check that it is practically negligible).
Right click on any of the three wires composing the circuit, select the List Currents command and click on the Current on Segment button of the displayed toolbar >. A table will be shown, where the current is tabulated vs. frequency. Next, press the Plot button to the right of the table to plot the current versus frequency, Fig. 3.
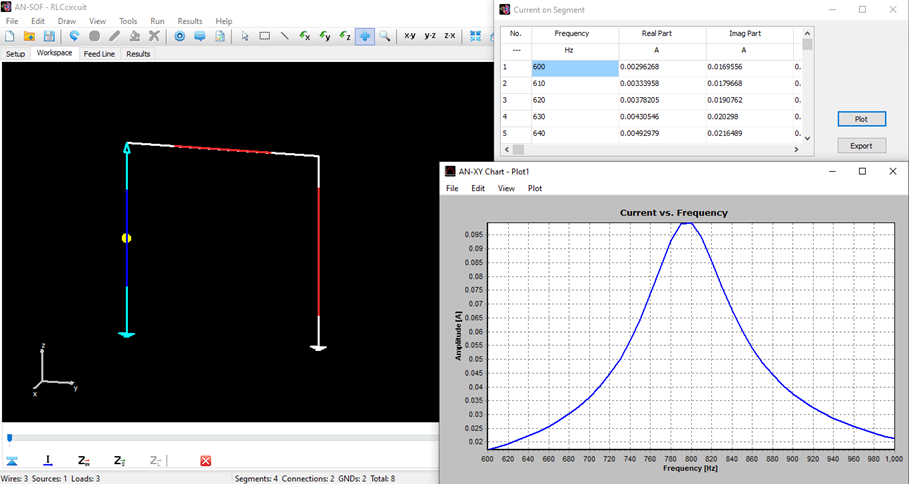
Since this is a series RLC circuit, the current flowing must be the same in all three wires (check this). As can be seen, resonance occurs at a frequency near to 800 Hz. Repeat the calculation for frequencies around 800 Hz, with a step of 1 Hz, and verify that the resonant frequency is 796 Hz. On the other hand, according to circuit theory, the resonance frequency is given by
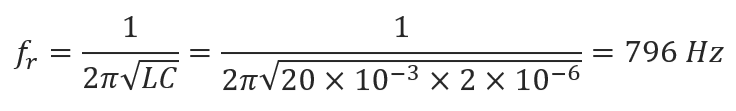
The agreement between AN-SOF and theory is remarkable!
Background Theory
The AN-SOF engine is written in the C++ programming language using double-precision arithmetic and has been developed to improve the accuracy in the modeling of wire antennas and metallic structures in general.
The computer code is based on an Electric Field Integral Equation (EFIE) expressed in the frequency domain. The current distribution on wire structures is computed by solving the EFIE using a Method of Moments (MoM) formulation with curved basis and testing functions, called the Conformal Method of Moments (CMoM) >. In this method, curved wires are modeled by means of conformal segments, which exactly follow the contour of the structure, instead of the traditional approximation based on straight wire segments. The linear approximation to the geometry can be a very inefficient method in terms of unknowns or computer memory. By using curved segments, the number of unknown currents, simulation time and memory space can be greatly reduced, allowing for the solution of bigger problems.
Old MoM codes suffer from several drawbacks due to the linear approximation to geometry and the use of the so-called thin-wire Kernel, such as: divergent input impedance, poor convergence for curved antennas (helices, loops, spirals) and bent wires, and singularities that appear when two parallel wires are close to each other or close to a lossy ground plane. With the CMoM and an exact Kernel formulation we have removed these limitations and obtained the following advantages:
- Decreased number of calculations and increased accuracy of results.
- Decreased simulation time and computer memory usage, allowing us to model larger and more complex designs.
- Ability to simulate from extremely low frequencies (circuits at 60 Hz) to very high ones (microwave antennas).
The current distribution on metallic surfaces with ideal conductivity can be found by solving an Electric Field Integral Equation (EFIE) expressed in the frequency domain:
where:
Ei: Incident Electric Field on the surface S.
n: unit vector at point r on the surface S.
k: wave number.
J: unknown electric current density flowing on the surface.
G: Green’s function, which in free space is given by:
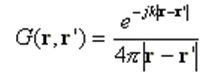
The EFIE is an expression of a boundary condition on the surface, namely zero tangential electric field. When we are dealing with a wire structure, the EFIE reduces to:
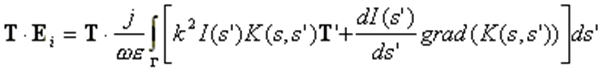
where T is the tangential unit vector describing the wire contour along its axis, I(s) is the unknown electric current on the wire, and K(s,s‘) is the integral equation Kernel defined as:
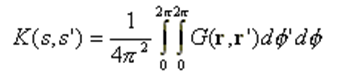
The EFIE is averaged about the wire circumference, resulting in the EFIE (3) with the Kernel (4). The current distribution I(s) is then the average value of the current density J in the axial direction; the current in the transversal direction is neglected. This is a good assumption provided that the wire radius is small with respect to the wavelength.
The wire axis is defined by its parametric equations that can be written in the compact form:
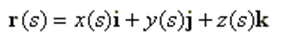
which points from the origin to any point on the wire, Fig. 1. The parameter s varies over a real interval. The tangent unit vector can be obtained from the first derivative of (5):
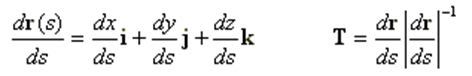
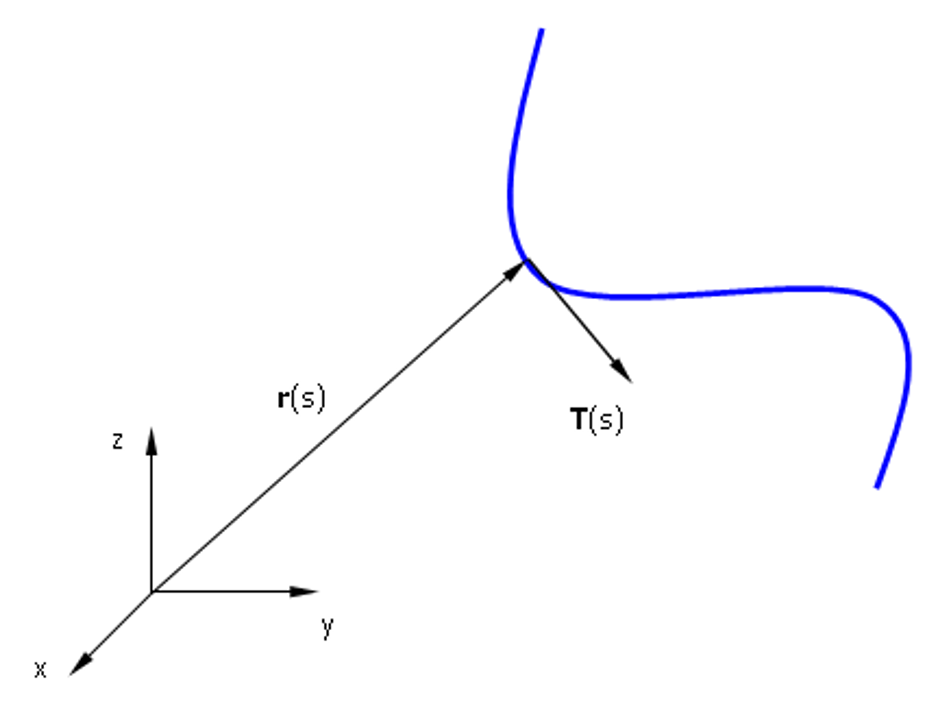
This parametric description is the key for the accurate modeling of wire structures. A straight wire approximation to the geometry produces a loss of geometrical information that can never be completely restored. However, this information is not lost if a parametric representation is used to describe the wire locus. It is also possible to improve on the straight wire approximation by using quadratic segments to model the geometry.
Thus, the definition of a wire must include its parametric description and its first derivative if an exact representation of the geometry is required, as shown in Fig. 1.
The Kernel (4) can be approximated by the following generalized thin-wire approximation:
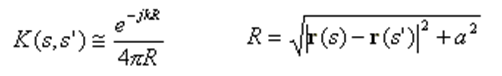
where a is the wire radius.
When the observation point r(s) and the source point r(s‘) are both in the same straight wire, the distance R reduces to the usual thin-wire approximation:
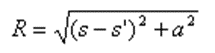
Thus, the EFIE and its Kernel are also valid for straight wires.
It is well known that the thin-wire approximation produces numerical oscillations in the computed current distribution near wire ends and near the position of discrete sources when wire segments are relatively thick. To avoid this undesired behavior and obtain the maximum accuracy, the exact Kernel in (4) is used in AN-SOF by default instead of the thin-wire approximation in (7). A closed-form expression for the exact Kernel has been found so its use practically does not compromise the speed of the simulation. However, an extended thin-wire Kernel has been calculated that also avoids the current distribution inaccuracies for a thin-wire ratio (wire diameter/segment length) < 3, which is far better than the thin-wire ratio < 1 that must be used when the standard thin-wire approximation is used.
In the Settings panel > of the Setup tabsheet check the Exact Kernel option to use the exact Kernel in (4). Uncheck this option to use the extended thin-wire Kernel.
The existence of a PEC ground plane is modeled in AN-SOF by means of image currents. This method can be easily implemented by adding an image term to the Green’s function, resulting in an additional term for the Kernel.
The kernel is the core of the integral equation that is solved in AN-SOF by means of the Method of Moments (MoM) to obtain the current distribution on metallic wires. Since the kernel cannot be calculated analytically in closed form, several approximations exist, among which the best known and widely used is the so-called thin-wire approximation.
The integral equation kernel is given by
$\displaystyle K(s,s’) = \frac{1}{4 \pi^2} \int_0^{2\pi} \int_0^{2\pi} G(\mathbf{r},\mathbf{r}’) \, d\phi’ d\phi \qquad (1)$
where $s$ and $s’$ are coordinates along a wire axis that represent an observation point and a source point, respectively. $G$ is the free space Green’s function, and $\phi$ and $\phi’$ are angles that determine points on the circumference of the wire cross-section. Thus, $\mathbf{r} = (s,\phi)$ represents an observation point on the wire surface, and $\mathbf{r}’ = (s’,\phi’)$ represents a source point. With that said, we can see that the kernel is obtained by averaging the Green’s function along the contour of the wire’s cross-section.
In the thin-wire approximation, the kernel is approximated as follows,
$\displaystyle K(s,s’) \approx \frac{e^{-j k R}}{4 \pi R}, \qquad R = \sqrt{|\mathbf{r}(s) \ – \ \mathbf{r}(s’)|^2 + a^2} \qquad (2)$
where $a$ is the wire radius, and $R$ is the distance between the source and observation points. When both points are on the same wire, the current will be represented by a filament on the wire axis, as the expression for $R$ shows. In particular, when both points coincide ($\mathbf{r} = \mathbf{r}’$), which happens when calculating the electromagnetic interaction of a wire with itself, the thin-wire kernel will vary as $1/a$, but the exact kernel will have an integrable singularity.
When a wire segment is thin, that is, its length is at least twice its diameter, the thin-wire approximation works well. However, as we increase the number of segments and therefore the segments get shorter, we will reach a threshold where the segments are too thick for the thin-wire approximation to work. This situation is particularly restrictive when we are investigating the convergence of some parameter or even when we want to fill the source gap at the antenna terminals using a short wire.
In AN-SOF, we have implemented the exact kernel instead of the thin-wire approximation. The solution involves separating the kernel into two terms: one containing an analytically integrable singularity, and the other containing a remainder that can be numerically integrated with minimal computational effort since it does not have any singularity. We have also provided the option of using an “extended kernel,” similar to the one used in NEC (Numerical Electromagnetics Code), where a series expansion of the kernel in terms of the wire radius is utilized, and the $a^2$ and $a^4$ terms are retained.
Note
In summary, it should be noted that AN-SOF implements both the Exact Kernel and the Extended Kernel, while NEC uses an extended kernel and the thin-wire approximation.
Fig. 1 shows the current distribution in amplitude along a center-fed half-wave dipole obtained using both the thin-wire approximation and the exact kernel. The antenna has been divided into segments with a diameter three times greater than their lengths, resulting in very thick wire segments in this case.
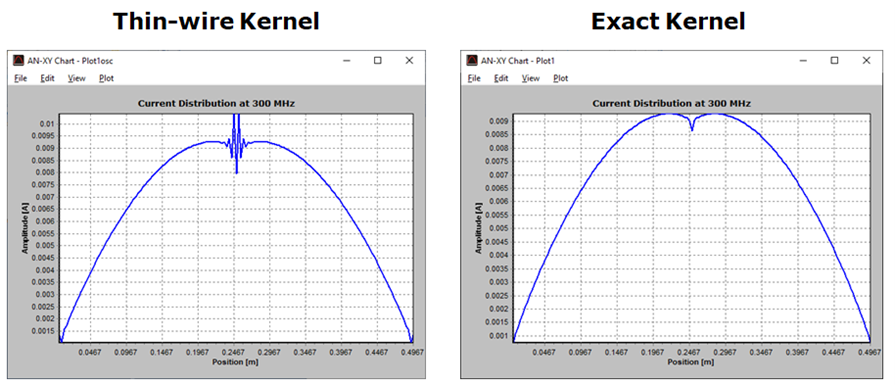
The thin-wire kernel exhibits the well-known oscillatory effect on the current distribution near the position of discrete sources and at wire ends for a segment diameter-to-length ratio greater than 1. As we can see, these oscillations disappear when the exact kernel is used instead of the thin-wire approximation.
The effect of not using the exact kernel can also be observed in the lack of convergence of the input impedance when the number of segments increases, as shown in Fig. 2 for the AN-SOF vs. NEC-2 results.
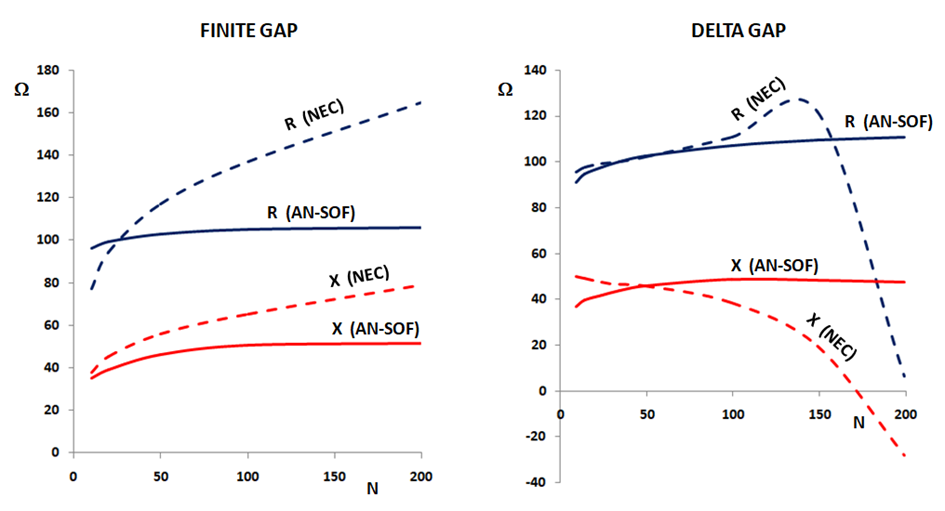
Note
In conclusion, we will achieve the highest possible accuracy in the calculation of the current distribution and antenna input impedance by using the Exact Kernel.
The Method of Moments (MoM) is a technique used to convert the EFIE into a system of linear equations that then can be solved by standard methods. For simplicity, the integral (linear) operator in the Electric Field Integral Equation > (EFIE) will be denoted by L. Then, the EFIE takes the form:
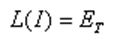
where ET is the tangential component of the incident electric field. The current distribution is approximated by a sum of N basis functions with unknown amplitudes In, giving:
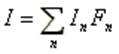
With this expansion and using the linearity of the operator L, we can write:
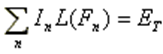
To obtain a set of N equations, the functional equation (3) is weighted with a set of N independent testing functions wm, giving:
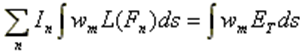
where the integrals are calculated over the domain of L. Now we have as many independent equations as unknowns, so (4) can be written as:
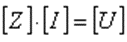
where
[Z]: impedance matrix with dimension NxN and the elements
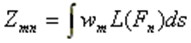
[I]: current matrix with dimension Nx1 and the elements In.
[U]: voltage matrix with dimension Nx1 and the elements
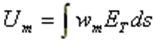
This fully occupied equation system must be solved for the unknown currents In. LU decomposition is used in AN-SOF. The MoM is applied by first dividing the wire structure into N segments, and then defining the basis and testing functions on the segments. Triangular basis and pulse testing functions are used in AN-SOF, Fig. 1.
When a curved wire is described parametrically by a vector function as in Eq. (5) here >, the basis and testing functions are curved in the sense that their support is a curved subset of the wire. Therefore, when curved basis and testing functions are used, the Conformal Method of Moments (CMoM) is obtained.
To fill the impedance matrix [Z], an adaptive Gauss-Legendre quadrature rule is applied to compute the involved integrals. After having solved the equation system, the currents In are known and other parameters of interest, such as input impedances, voltages, radiated power, directivity, and gain can be computed.
The MoM can also be used to calculate the electromagnetic response of metallic surfaces, which are modeled using wire grids. In AN-SOF, with the CMoM the accuracy of the calculation of wire grids is remarkably improved compared to the traditional MoM, as demonstrated in this article > . Another extension of the calculation includes wires that do not have a circular cross section. In AN-SOF an equivalent radius is calculated for these wires.
If a discrete voltage source is placed at the i-th segment, the corresponding element in the voltage matrix is simply equal to the voltage of the generator. Thus,
When an incident plane wave is used as the excitation, each wire segment is excited by the incoming field, which has the form:
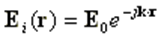
where k is defined by the direction of propagation, so that |k| = k is the wave number, and r is the evaluation point, Fig. 1. The elements of the voltage matrix are then defined by:
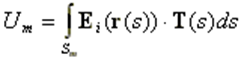
where the integration is performed over the m-th segment, and the vectors r(s) and T(s) are given by Eqs. (5) and (6) here >.
Many examples show the advantages of using curved segments with respect to the stability and convergence properties of the solutions. Due to the improved convergence rate, accurate results can be obtained with reduced simulation time and memory space.
Fig. 1 shows the dimensions of a center-fed helical antenna in free space (normal mode). Figs. 2 and 3 show a comparison between AN-SOF, which uses curved segments, and a straight wire approximation to the helix of Fig. 1. The convergence properties of the input impedance and admittance versus the number of segments are investigated.
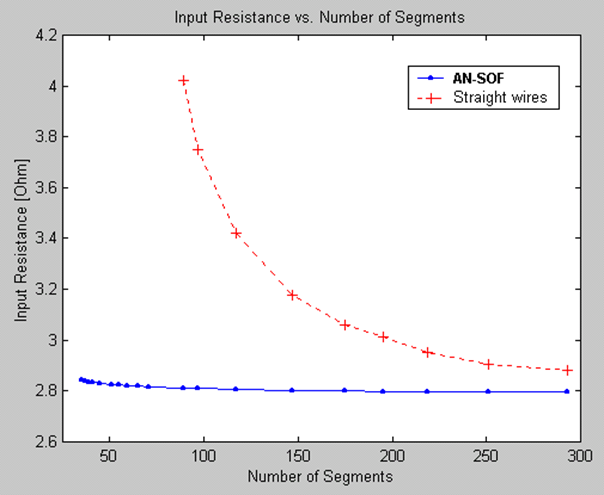
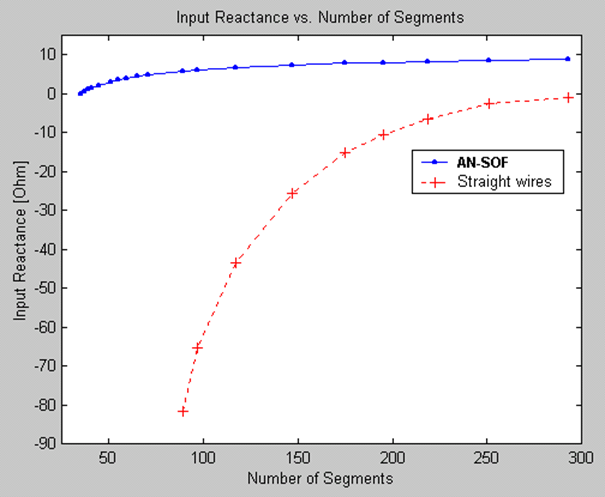
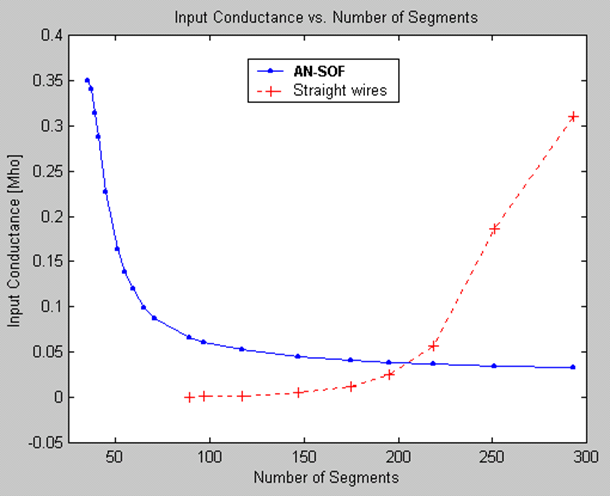
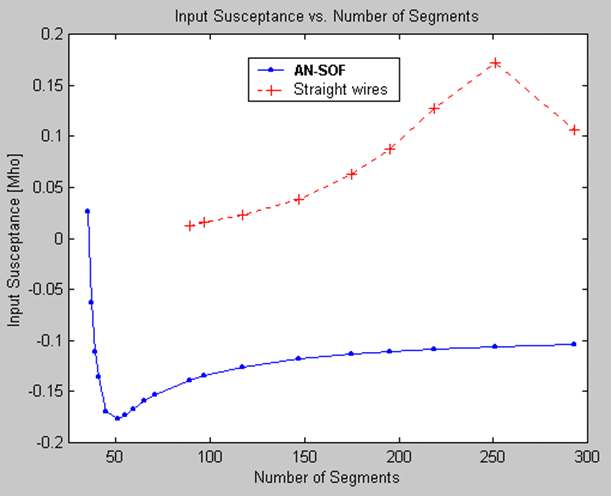
As can be seen from these results, by using curved segments significantly fewer unknowns are needed to predict the input impedance. However, the admittance convergence is questionable for the straight wire case, while it has a notorious convergent behavior for the curved case.
The improvement depends on the geometry and frequency, but generally, if N straight segments are needed to obtain a convergent value, then N/p curved segments are needed to obtain the same value, with p = 2…10. For a straight geometry the improvement factor is p = 1, as can be expected, because there are no curved segments in this case.
Frequently Asked Questions
No, you don’t. Simply run AN-SOF and start using it. If prompted for a license, go to the AN-SOF main menu > Help > Activation Key. Click the Trial Key button in the displayed window, followed by the Activate button. AN-SOF will restart and be ready for use in trial mode.
The trial period lasts 30 days, during which software evaluation support is available. However, you can continue using AN-SOF Trial after the evaluation period ends.
The Trial version is limited to 50 segments (wire segments + wire-to-wire junctions + wire-to-ground connections) for calculations. However, all example files included in the installation directory are pre-computed and can be opened without restrictions to display tables and graphs.
You can also download additional example files with fewer than 50 segments from this link.
No, AN-SOF PRO is a lifetime license and will continue to function on the same PC where it was installed and activated, even after your plan expires. However, if you choose not to renew your plan, you will no longer have access to the following:
- Software Updates: You will no longer be able to download the latest versions, including bug fixes and security updates.
- Technical Support: You will no longer receive technical assistance from our team.
- Installer Access: Installers for discontinued versions will only be available for 3 years after discontinuation. After this period, they will no longer be provided. As technology evolves, we cannot guarantee long-term compatibility.
- Activation Key Replacement: If you lose your activation key for a discontinued version or need to transfer AN-SOF to another PC, we cannot issue a new key more than three years after the version has been discontinued.
While AN-SOF will continue to work on your installed PC (assuming the OS remains unchanged), we recommend renewing your plan to ensure access to the latest features, technology improvements, and ongoing support.
If you don’t renew your plan, the following will apply:
- Continued Functionality: AN-SOF will keep working on the same PC where it was installed and activated, but only with the last version available before your plan expired.
- No Updates: You won’t receive new versions, bug fixes, security patches, or feature updates.
- Limited Support: Technical support will no longer be available.
- Version Discontinuation: Your installed version will eventually be discontinued. Three years after discontinuation, its installer and activation key will no longer be available.
To maintain full functionality, updates, and support, we recommend renewing your plan before it expires. Customers who renew early receive special benefits and discounts.
Due to the availability of a fully functional trial version with no time limit, all sales of AN-SOF software licenses are final and non-refundable. This policy helps us ensure that users have a fair opportunity to try out the software before making a purchase. We encourage all users to thoroughly evaluate the trial version before purchasing a license. You can find detailed information about the conditions and process for exceptions to the non-refundable policy on our dedicated Refund Policy page.
No, consulting services are not included, as we do not offer consulting of any kind. However, our technical support—available with both plans—goes beyond resolving software issues. We assist customers in improving their models and expanding their understanding of antenna modeling techniques to maximize the capabilities of AN-SOF. While we provide tips and guidance, this should not be considered consulting.
Windows Vista/7/8/10/11. 2GHz CPU, 2GB RAM, 1GB free disk space.
The supported operating system is Microsoft Windows. We have no plans to release a Mac version. Macintosh users can run a program called Parallels >. Parallels Desktop for Mac is desktop virtualization software that allows Microsoft Windows applications to run on an Apple Mac computer.
No. The supported operating system is Microsoft Windows. We have no plans to release a Linux version. You can use a Windows emulator like Wine, CrossOver Linux, Vmware Workstation or whatever you find on the market.
No, it doesn’t. AN-SOF has been developed to run on home computers running Windows(R) OS, so numerical calculation strategies have been implemented to take care of the available RAM memory and at the same time obtain reliable results.
AN-SOF does not have a fixed upper frequency limit. What matters is the electrical size of the structure, meaning its dimensions measured in wavelengths, rather than the specific frequency or band. As the structure becomes larger in terms of wavelengths, the size of the matrix equation to be solved increases, which requires more memory and computation time on a given PC. In practice, the limit is determined by your computer resources and the electrical size of the model, not by frequency itself.
By default, AN-SOF calculates the minimum recommended number of segments for each wire depending on its length in wavelengths. Various convergence analyzes > show that 10 wire segments per wavelength is sufficient for most cases. Regarding tapered wires, in old algorithms like NEC it was necessary to increase the density of segments near the connections between wires when there is a radius jump. This is not necessary in AN-SOF as it is not NEC based. See the advantages of AN-SOF here >.
Yes. Go to main menu > Edit > Copy Wires > to duplicate or make the desired number of copies of the selected wires. There is also the Stack Wires command which allows us to repeat a design along a given direction. By using this command in combination with the Scale Wires > command we can quickly build Yagi-like arrays.
Yes. Parametric design is possible by running a Bulk Simulation >. We prefer that the user chooses the programming language to generate a sequence of files in NEC format with one or more variable parameters. Calculations on these files can then be run automatically in bulk. Scilab > is a free numerical calculation software tool with which we can program scripts that generate multiple descriptions of an antenna with variable parameters. Download an example of a Yagi-Uda antenna with variable element spacing from this link >.
In addition to specializing in wire structures composed of wire grids, AN-SOF also allows the modeling of solid metallic surfaces. Solid surfaces are viewed in the AN-SOF workspace as if they were wire grids; however, they are actually made up of flat strips. These strips have widths automatically calculated to completely cover a metal surface without leaving holes. Currently, there is a limit in the size of the grid/surface that can be modeled (see FAQ #10).
AN-SOF is equipped to model solid metallic surfaces, including parabolics and horns. Currently, there is a limitation of approximately 10 square wavelengths of surface. As long as your antenna’s surface area stays within this threshold, you can run simulations. This limitation pertains to the surface area of the antenna measured in square wavelengths, rather than a restriction on the frequency range. This limitation also applies to grids (patches, plates, cylinders, spheres, etc.).
Yes, it does. Resistance, inductance, and capacitance elements can be added to the structure to model the connection of lumped load impedances.
Yes, they are. The computed near E and H fields can be visualized in 2D and 3D plots as well as in tables and exported as CSV (Comma Separated Values) files. Cartesian, cylindrical and spherical near field components can be obtained.
No. AN-SOF is an independent implementation of the Method of Moments (MoM) for wire structures. NEC is an old Fortran calculation engine that has a lot of limitations. Many of these limitations have been removed in AN-SOF by implementing the so-called Conformal Method of Moments with Exact Kernel > in a completely new object-oriented C++ code. See further details here >.
Yes. Most of the NEC commands are supported. Download NEC example files to import into AN-SOF from here >.
Dielectric material can be added as insulation or coating to metallic wires, and microstrip antennas can be patterned on a dielectric substrate. However, modeling volumes composed entirely of dielectric materials is not currently supported.
While AN-SOF was originally designed for simulating wire structures using the Method of Moments (MoM), its calculation engine has been extended to support simple PCB and microstrip antenna designs that meet the following requirements. For structures that do not comply with these conditions, a Finite Element Method (FEM) solver (not included in AN-SOF) should be used instead.
Key Limitations & Requirements:
- Single-Layer, Lossless Substrate Only
- Only one dielectric layer is supported (multilayer substrates are not).
- The substrate must be lossless (loss tangent is assumed zero).
- No holes or cutouts are permitted in the substrate.
- Finite-Size Substrate Constraints
- The substrate must be rectangular.
- Traces must be at least 5× the trace width away from the substrate edges.
- Ground Plane & Vias
- A perfect electric conductor (PEC) ground plane is mandatory and cannot be removed.
- Vertical vias can be modeled as short vertical wires connecting traces to the ground plane (e.g., for antenna feeding).
- No Slot-Based Designs
- Slot antennas or patches with slots cannot be modeled due to software limitations.
We currently have no plans to integrate an FEM solver into AN-SOF. For advanced PCB or antenna designs—such as multilayer structures, lossy substrates, or slotted geometries—we recommend using alternative simulation tools.
You have entered an invalid activation key. Find the AN-Key app and launch it. Press the “Trial Key” button and then “Activate”. Restart AN-SOF. Follow the instructions in the AN-Key window to request a valid key corresponding to your serial number if you have purchased a license. Please note that the key you used to activate a previous version of AN-SOF may not be valid for the latest version. Request a new key >.
Find the AN-Key app and launch it. Press the “Trial Key” button and then “Activate”. Restart AN-SOF. Follow the instructions in the AN-Key window to request a valid key corresponding to your serial number if you have purchased a license. Please note that the key you used to activate a previous version of AN-SOF may not be valid for the latest version. Request a new key >.
Uninstall AN-SOF. Then go to C:\ and delete all the folders whose names start with “AN-SOF Professional”. Reinstall AN-SOF. Find the AN-Key app and launch it. Follow the instructions in the AN-Key window to request a valid key corresponding to your serial number if you have purchased a license. If the problem persists, open a support case here >. Please note that the key you used to activate a previous version of AN-SOF may not be valid for the latest version. Request a new key >.
Uninstall AN-SOF. Then go to C:\ and delete all the folders whose names start with “AN-SOF Professional”. Reinstall AN-SOF.
Press Ctrl + Alt + Del and run the Task Manager. Right click on the application that is not working and choose “End Task”.
Navigate to the folder that you specified when using the installer. The default folder is “C:\AN-SOF Professional X”, where X is the AN-SOF version. Then, launch ANSOF.exe directly from that location. You can create a shortcut to this file on the Windows desktop if you wish.
Indexed Articles
- 1.3 Arrays of Point Sources
- Adding a Real Ground Plane
- Adding a Custom Lossy Line
- Adjusting the Color Bar in AN-3D Pattern
- A Closer Look at the HF Skeleton Slot Antenna
- Aborting the Calculations
- Adding a Dielectric Substrate
- Adding a Feed Line and Transformer
- Adding a PEC Ground Plane
- Adding Loads
- Adding Sources
- Adding Transmission Lines
- Advantages of AN-SOF for Simulating 433 MHz Spring Helical Antennas for ISM & LoRa Applications
- An Efficient Approach to Simulating Radiating Towers for Broadcasting Applications
- An RLC Circuit
- AN-SOF 7.0 is Here!
- AN-SOF 7.20 is ready!
- AN-SOF 7.80 is ready!
- AN-SOF 8.70: Enhancing Your Antenna Design Journey
- AN-SOF 8: Elevating Antenna Simulation to the Next Level
- AN-SOF 9.50 Release: Streamlining Polarization, Geometry, and EMF Calculations
- AN-SOF 9: Taking Antenna Design Further with New Feeder and Tuner Calculators
- AN-SOF Antenna Simulation Best Practices: Checking and Correcting Model Errors
- AN-SOF Antenna Simulation Software - Version 8.90 Release Notes
- AN-SOF Data Export: A Guide to Streamlining Your Workflow
- AN-SOF Engine User Guide
- AN-SOF Implements James R. Wait Theory for Ground Losses of LF/MF Radio Masts
- AN-SOF in Action: Modeling and Understanding the Performance of Fractal Antennas
- AN-SOF Mastery: Adding Elevated Radials Quickly
- AN-SOF Overview
- AN-SOF User Guide
- Antennas on a Ship
- Arc
- Archimedean Spiral
- Articles Index Directory
- A Simple, Low-Cost Approach to Simulating Solid Wheel Antennas at 2.4 GHz
- A Transmission Line
- Automating 2-Element Quad Array Design: Scripting and Bulk Processing in AN-SOF
- Automotive Antenna Placement: How Vehicle Geometry Reshapes FM Reception
- 2.7 Beamwidth and Sidelobes
- Beyond Analytical Formulas: Accurate Coil Inductance Calculation with AN-SOF
- Boosting Performance with Dual V Antennas: A Practical Design and Simulation
- Building a Beam: Modeling a 5-Element 2m Band Quad Array
- Building a Compact High-Performance UHF Array with AN-SOF: A 4-Element Biquad Design
- Building Effective Cost Functions for Antenna Optimization: Weighting, Normalization, and Trade-offs
- 3.1 Cylindrical Wire Antennas
- Calculating the Current Distribution
- Calculating the Far Field
- Calculating the Near E-Field
- Calculating the Near H-Field
- Can AI Design Antennas? Lessons from a 3-Iteration Yagi-Uda Experiment
- Capacitively-Fed Patch
- Circle
- Complete Workflow: Modeling, Feeding, and Tuning a 20m Band Dipole Antenna
- Cone
- Conformal Method of Moments
- Connecting Transmission Lines
- Connecting Wires
- Connecting Wires to the Ground
- Convergence of the Dipole Input Impedance
- Copying and Stacking Wires
- Cross-Section Equivalent Radius
- Curved vs. Straight Segments
- Custom Feed Line Options
- Custom Preferences
- Custom Transmission Lines
- Cylinder
- 5.2 Differential Equation Methods
- 2.6 Directivity and Gain
- Defining the Environment
- Defining the Excitation
- Deleting a Grid/Surface
- Deleting a Wire
- Deleting Multiple Wires
- Design and Analysis of a Parabolic Cylinder Reflector with a Back-Firing Primary Radiator
- Design and Simulation of Short Top-Loaded Monopole Antennas for LF and MF Bands
- Design Guidelines for Skeleton Slot Antennas: A Simulation-Driven Approach
- Dipole Gain and Radiation Resistance
- Disc
- Disclaimer of Warranty
- Dish Antenna
- Displaying Smith Charts
- DIY Helix High Gain Directional Antenna: From Simulation to 3D Printing
- Download Examples
- 2.11 Effective Aperture and Gain
- 3.6 Equivalent Radius for Non-Circular Wires
- Editing Loads
- Editing Sources
- Editing Transmission Lines
- Efficient NOAA Satellite Signal Reception with the Quadrifilar Helix Antenna
- Electric Field Integral Equation
- Element Spacing Simulation Script for Yagi-Uda Antennas
- Enabling/Disabling Coating
- Enabling/Disabling Loads
- Enabling/Disabling Resistivity
- Enhanced Methodology for Monopoles Above Radial Wire Ground Screens
- Enhancing Antenna Design Flexibility: Project Merging in AN-SOF
- Enhancing VHF Performance: The Dual Reflector Moxon Antenna for 145 MHz
- Evaluating EMF Compliance - Part 1: A Guide to Far-Field RF Exposure Assessments
- Evaluating EMF Compliance - Part 2: Using Near-Field Calculations to Determine Exclusion Zones
- Evolving Better Antennas: A Genetic Algorithm Optimizer Using AN-SOF and Scilab
- Excitation by an Incident Field
- Excitation of the Structure
- Experimenting with Half-Wave Square Loops: Simulation and Practical Insights
- Explicit Modeling of a 9-Element LPDA: Capturing Real-World Wideband Performance
- Explore 5 Antenna Models with Less Than 50 Segments in AN-SOF Trial Version
- Explore the Cutting-Edge World of AN-SOF Antenna Simulation Software!
- Exploring an HF Log-Periodic Sawtooth Array: Insights from Geometry to Simulation
- Exploring the Spiral Loop Antenna: A Compact Solution for 80m DXing
- Exporting Currents on a Wire
- Exporting the Far Field
- Exporting the Near Field
- Exporting Wires
- Export Radiation Patterns to MSI Planet
- Export Radiation Patterns to Radio Mobile
- Extended Double Zepp (EDZ): A Phased Array Solution for Directional Antenna Applications
- 2.8 Feedpoint Impedance and Bandwidth
- 4.7 Fractal Antennas
- Far Field Parameters
- Fast Modeling of a Monopole Supported by a Broadcast Tower
- Feeder Results: Input Impedance and Losses
- File Formats
- Flat Ring
- Fractal vs. Arbitrary Geometry: Analyzing the VE9SRB "Random" Loop
- Front-to-Rear and Front-to-Back Ratios: Applying Key Antenna Directivity Metrics
- 3.3 Induced EMF Method
- 3.2 Input Impedance and Feedpoint Modeling
- 5.3 Integral Equation Methods
- 5.1 Introduction to Antenna Simulation
- Importing Wires
- Incident Field Parameters
- Input Impedance and Directivity of Large Circular Loops
- Internal Impedance of a Source
- Introducing AN-SOF 10.5 – Smarter Tools, Faster Workflow, Greater Precision
- Introducing AN-SOF 8.50: Enhanced Antenna Design & Simulation Software
- Introducing the AN-SOF Engine: Power, Speed, and Flexibility for Antenna Simulation
- Introduction to Yagi-Uda Arrays: Analyzing a 5-Element Beam with a Folded Dipole Driver
- 4.4 Log-Periodic Arrays
- 4.1 Loop Antennas
- Licensing FAQ
- Line
- Linear Antenna Theory: Historical Approximations and Numerical Validation
- Linking Log-Periodic Antenna Elements Using Transmission Lines
- Listing Load Impedances
- Listing the Currents in a Segment
- Listing the Input Impedances, VSWR, and S11
- Logarithmic Spiral
- 5.5 Method of Moments (MoM)
- 1.9 Monopole Antennas
- 4.8 Microstrip and Printed Antennas
- 1.1 Maxwell’s Equations and Electromagnetic Radiation
- Microstrip Antenna Array
- Microstrip Dipole
- Modeling a Center-Fed Cylindrical Antenna with AN-SOF
- Modeling a Circular Loop Antenna in AN-SOF: A Step-by-Step Guide
- Modeling an Inverted V Antenna for 40 Meters: Design Insights and Ground Effects
- Modeling a Super J-Pole: A Look Inside a 5-Element Collinear Antenna
- Modeling Coaxial Cables
- Modeling Common-Mode Currents in Coaxial Cables: A Hybrid Approach
- Modeling Helix Antennas in Axial Radiation Mode Using AN-SOF
- Modifying a Grid/Surface
- Modifying a Wire
- Monopole Antennas Over Imperfect Ground: Modeling and Analysis with AN-SOF
- Moving, Rotating, and Scaling Wires
- 4.6 Parabolic Reflectors
- 2.2 Polarization
- Paraboloid
- Patch
- Patch Antenna
- Plate
- Plotting 2D Far Field Patterns
- Plotting 3D Far Field Patterns
- Plotting Near Field Patterns
- Plotting the Current Distribution
- Plotting the Far Field Spectrum
- Plotting the Near Field Spectrum
- Power Budget
- Precision Simulations with AN-SOF for Magnetic Loop Antennas
- Project Details
- 2.3 Radiated Power and Energy Conservation
- 2.5 Radiation Efficiency
- 2.1 Radiation Pattern Fundamentals
- 2.4 Radiation Resistance
- 2.10 Receiving Mode Operation
- Radar Cross Section
- Radar Cross Section and Reception Characteristics of a Passive Loop Antenna: A Simulation Study
- Radiation Resistance and Directivity of Small Loops
- RCS of Aircraft
- Removing the Ground Plane
- RF Calculators
- RF Techniques: Implicit Modeling and Equivalent Circuits for Baluns
- Running a Bulk Simulation
- 3.7 Self and Mutual Impedances
- Scilab Script for Plotting Level Curves
- Selecting and Modifying Multiple Wires
- Selecting a Wire
- Shortcut Keys
- Simple Dual Band Vertical Dipole for the 2m and 70cm Bands
- Simplified Modeling of Microstrip Antennas on Ungrounded Dielectric Substrates: A Practical First-Order Approach
- Simulating a Multiband Omnidirectional Dipole Antenna Design
- Simulating Helical Antennas over Finite Wire-Grid Ground Planes
- Specifying the Frequencies
- Sphere
- Step-by-Step: Modeling Basic Yagi-Uda Arrays for Beginners
- 2.12 The Friis Transmission Equation
- 1.6 The Half-Wave Dipole
- 1.4 The Hertzian Dipole – FREE SAMPLE
- 1.2 The Isotropic Radiator
- 2.9 The Reciprocity Principle
- 1.5 The Short Dipole
- 1.7 Thin Dipoles of Arbitrary Length
- 1.0 Table of Contents
- Tabular Input of Linear Wires
- Tapered Wires
- Technical FAQ
- The 17m Band 2-Element Delta Loop Beam: A Compact, High-Gain Antenna for DX Enthusiasts
- The 3D-View Interface
- The 5-in-1 J-Pole Antenna Solution for Multiband Communications
- The AN-SOF Calculation Engine
- The AN-SOF Interface
- The Conformal Method of Moments
- The Exact Kernel
- The Lazy-H Antenna: A 10-Meter Band Design Guide
- The List Currents Toolbar
- The Loop on Ground (LoG) Antenna: A Compact Solution for Directional Reception
- The MI2 Fractal Loop: Achieving Resonant Efficiency in Compact Apertures
- The Moxon-Yagi Dual-Band VHF/UHF Antenna for Superior Satellite Link Performance
- The Plots Tab
- The Results Tab
- The Run ALL Command
- The Settings Panel
- The Setup Tab
- The Source/Load/TL Toolbar
- Tools in the Workspace
- To Our Valued AN-SOF Customers and Users: Reflections, Milestones, and Future Plans
- Transmission Line Feeding in Antenna Design: Exploring the Four-Square Array
- Troubleshooting
- Truncated Cone
- Tuner for Impedance Matching
- Types of Excitations and Loads
- Types of Grids and Surfaces
- Types of Results
- Types of Wires
- Navigating the Numerical Landscape: Choosing the Right Antenna Simulation Method
- Near Field Parameters
- Nelder-Mead Optimization for Antenna Design Using the AN-SOF Engine and Scilab
- New AN-SOF User Guide
- New Release :: AN-SOF 6.20 ::
- New Release :: AN-SOF 6.40 ::
- New Release :: AN-SOF 7.10 ::
- New Release: AN-SOF 7.50
- New Release: AN-SOF 7.90
- New Tools in AN-SOF: Selecting and Editing Wires in Bulk
- Numerical Green's Function
This Knowledge Base and associated software are provided “as is” without warranty of any kind, expressed or implied. Golden Engineering LLC disclaims all warranties, including, but not limited to, the implied warranties of merchantability, fitness for a particular purpose, and non-infringement.
Golden Engineering LLC does not warrant that:
- The technical descriptions, procedures, and software are free from errors or defects.
- The equations, programs, and procedures are consistent with any standard of merchantability.
- The equations, programs, and procedures will meet your requirements for any application.
Golden Engineering LLC is not liable for any damages arising from the use of the Knowledge Base or associated software, including, but not limited to:
- Direct, indirect, incidental, consequential, or punitive damages.
- Damages for loss of profits, data, or use.
- Damages for personal injury or property damage.
Any use of the Knowledge Base or associated software is at your own risk.
